
- •Тема 1. Концептуальні аспекти математичного моделювання економіки.
- •Тема 2. Оптимізаційні економіко-математичні моделі. Практичне заняття №1
- •Задача 1.
- •Задача 2.
- •Задача 3.
- •Задача 4.
- •Задача 5.
- •Задача 6.
- •Тема 1. Концептуальні аспекти математичного моделювання економіки.
- •Тема 2. Оптимізаційні економіко-математичні моделі. Лабораторне заняття №1
- •Постановка задачі:
- •Порядок розв’язання:
- •Задача 1
- •Тема 3. Задача лінійного програмування та методи її розв’язування. Практичне заняття №2
- •Задача 1.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Приклад1.
- •Задача 1.
- •Тема 3. Задача лінійного програмування та методи її розв’язування. Лабораторне заняття №3
- •Постановка завдання:
- •Задача 1.
- •Тема 3. Задача лінійного програмування та методи її розв’язування. Лабораторне заняття №4
- •Алгоритм розв’язування задач лп з використанням процедури «Пошук рішення»
- •Задача 1.
- •Задача 2.
- •Задача 3.
- •Задача 4.
- •Задача 5.
- •Задача 6.
- •Тема 3. Задача лінійного програмування та методи її розв’язування. Практичне заняття №4
- •Задача 1.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Задача 1
- •Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач. Практичне заняття №5
- •Постановка завдання:
- •Приклад 1
- •Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач.
- •Приклад1.
- •Задача 1
- •Задача 2
- •Лабораторне заняття № 7. Мкр 1.
- •Тема 6.Нелінійні оптимізаційні моделі економічних систем. Практичне заняття №7
- •Тема 6.Нелінійні оптимізаційні моделі економічних систем. Практичне заняття №8
- •Тема 5. Цілочислове програмування.
- •Тема 5. Цілочислове програмування.
- •Метод Гоморі
- •Приклад1.
- •Тема 7. Аналіз та управління ризиком в економіці.
- •Тема 7. Аналіз та управління ризиком в економіці.
- •Тема 7. Аналіз та управління ризиком в економіці.
- •Приклад 1.
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем.
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем.
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем.
- •Необхідні та достатні умови безумовного екстремуму функції. Необхідні умови першого порядку
- •Задача 1
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем. Лабораторне заняття №12
- •Постановка завдання:
- •Стратегія вирішення задачі
- •Задача 1
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем. Лабораторне заняття №13.
- •Лабораторне заняття №14. Мкр 2.
- •Тема 8. Система показників кількісного оцінювання ступеня ризику. Практичне заняття №13.
- •Задача 1
- •Задача 2
- •Задача 3.
- •Задача 4.
- •Задача 5.
- •Задача 6.
Тема 7. Аналіз та управління ризиком в економіці.
ПРАКТИЧНЕ ЗАНЯТТЯ №10
Тема заняття: Розв’язання задач теорії ігор.
Знаходження сідлової точки. Відбір домінуючих стратегій.
Мета: сформувати вміння та навички розв’язання задач теорії ігор, знаходження сідлової точки та відбору домінуючих стратегій.
Методичні рекомендації: Вивчити лекцію №6 та ознайомиться з наступною літературою [3 с. 224-250], [4 с. 239-251].
Задача 1
Визначити ціну гри та оптимальні стратегії гри, заданої платіжною матрицею:
1.1.
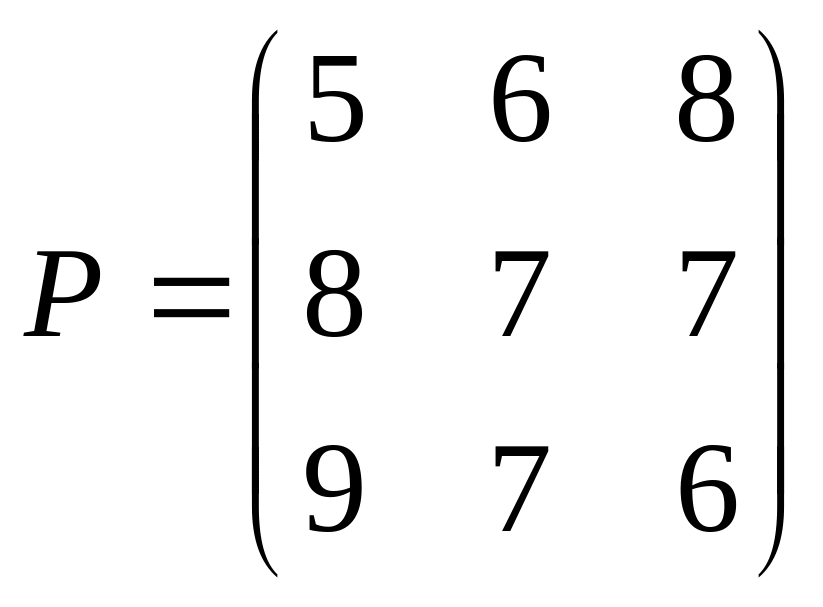 ;
1.2.
;
1.2.
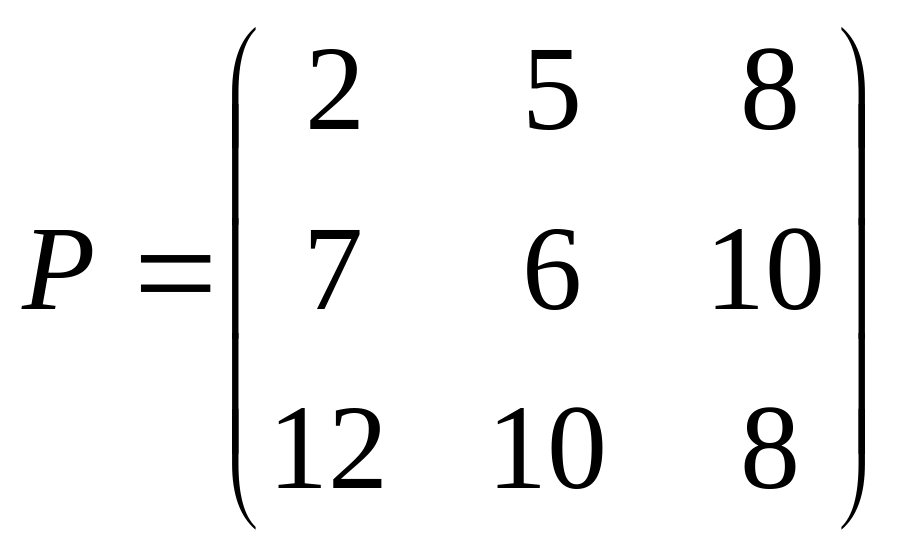 ;
;
1.3.
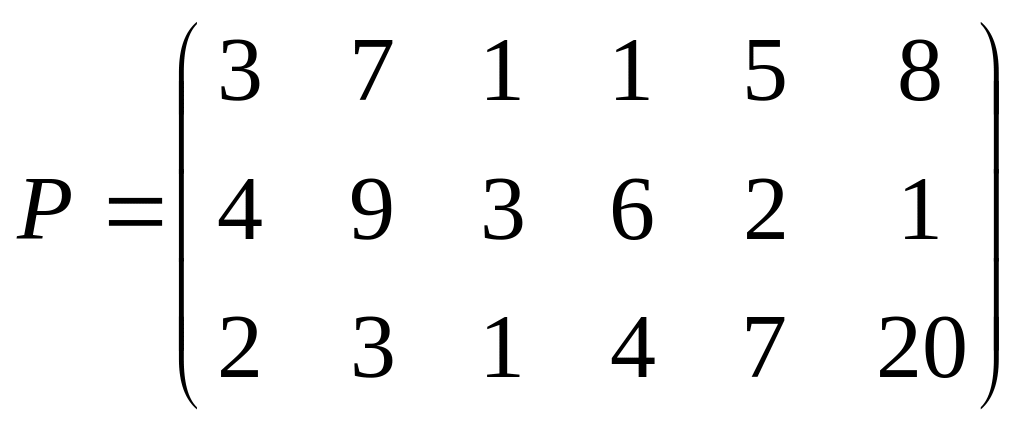 ;
1.4.
;
1.4.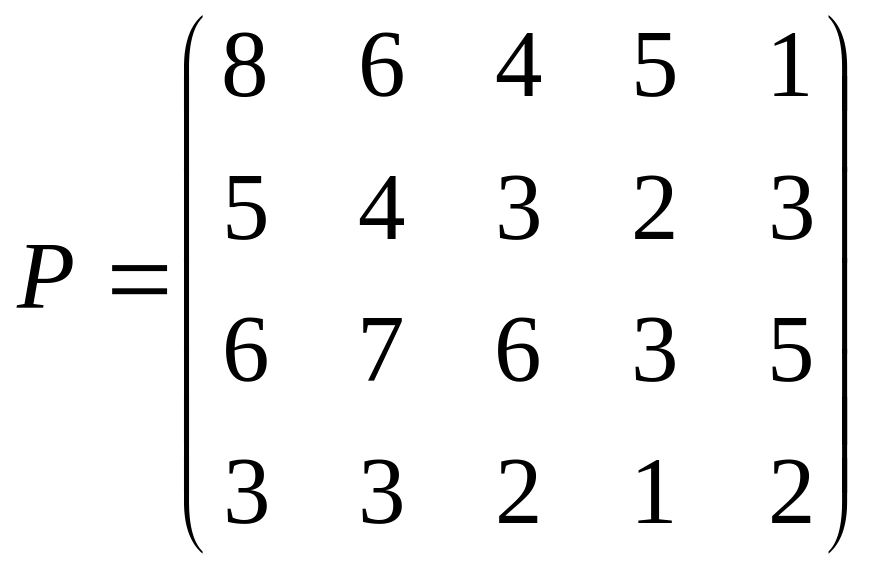 .
.
ДОДАТКОВІ ЗАВДАННЯ:
Задача 2
Визначити ціну гри та оптимальні стратегії гри, заданої платіжною матрицею:
 .
.
Тема 7. Аналіз та управління ризиком в економіці.
ПРАКТИЧНЕ ЗАНЯТТЯ № 11
Тема заняття: Розв’язання задач теорії ігор.
Графічний метод розв’язання задач теорії ігор розміром 2x2, 2xn, mx2.
Мета: сформувати вміння та навички розв’язання задач теорії ігор розміром 2x2, 2xn, mx2 графічним методом.
Методичні рекомендації: Вивчити лекцію №6 та ознайомиться з наступною літературою [3 с. 224-250], [4 с. 239-251].
Задача 1
Визначити оптимальні стратегії і ціну гри, використовуючи геометричну інтерпретацію:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
;
1.3.
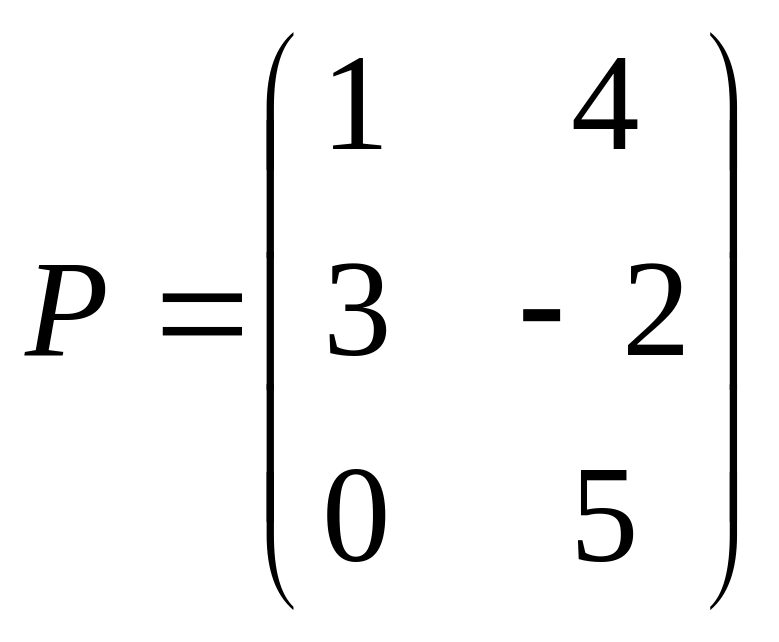 ; 1.4.
; 1.4.
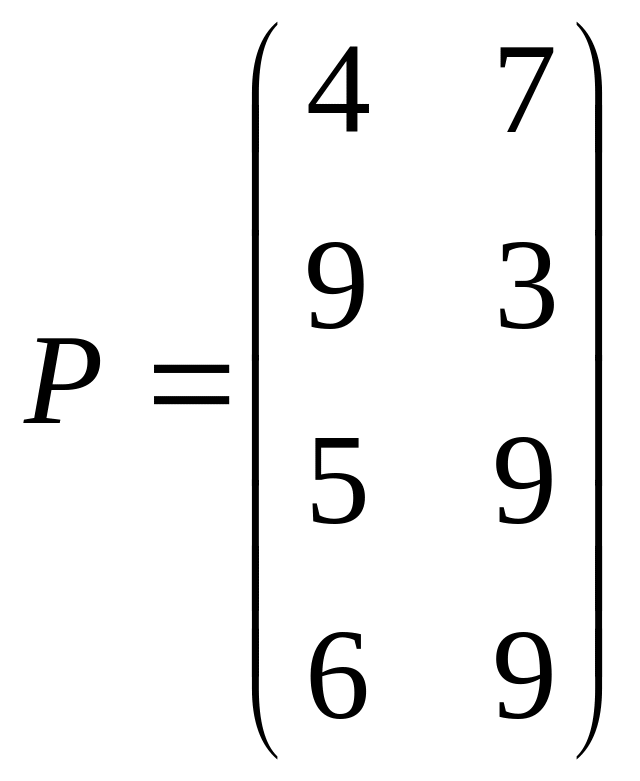 .
.
ДОДАТКОВІ ЗАВДАННЯ:
Задача 2
Визначити оптимальні стратегії і ціну гри, використовуючи геометричну інтерпретацію:
2.1.
![]() ;
2.2.
;
2.2.
![]()
Тема 7. Аналіз та управління ризиком в економіці.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №9
Тема заняття: Розв’язання задач теорії ігор.
Зведення задач теорії ігор до задач ЛП та вирішення останніх симплексним методом.
Мета: сформувати вміння та навички розв’язання задач теорії ігор симплексним методом.
Методичні рекомендації: Вивчити лекцію №6 та ознайомиться з наступною літературою [3 с. 224-250], [4 с. 239-251].
Постановка завдання:
Якщо матрична гра не має сідлової точки, то знаходження її розв’язку, особливо за великої кількості стратегій, — доволі складна задача, яку можна ефективно розв’язати методами лінійного програмування.
Задача
розглядається в такому формулюванні:
знайти вектори ймовірностей
![]() і
і
![]() з метою визначення оптимального значення
ціни гри та оптимальних стратегій.
з метою визначення оптимального значення
ціни гри та оптимальних стратегій.
Зауважимо, що доведено основну теорему теорії ігор: кожна скінчена гра має принаймні один розв’язок, який можливий в області змішаних стратегій.
Отже, нехай маємо скінченну матричну гру з платіжною матрицею
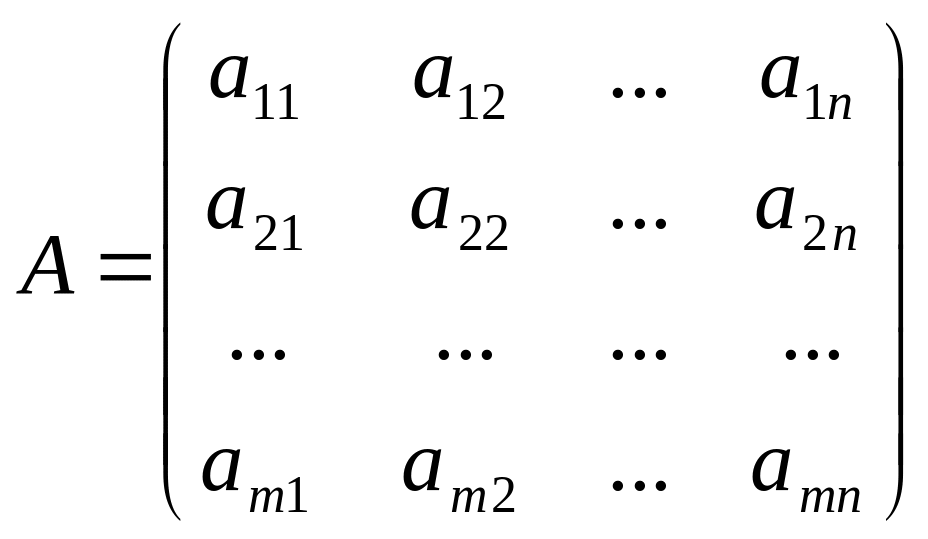 .
.
Оскільки оптимальні стратегії гравців А і В дозволяють отримати виграш
![]() ,
,
то використання оптимальної змішаної стратегії гравцем А має забезпечувати виграш не менший за ціну гри в разі вибору гравцем В будь-яких стратегій. Математично ця умова записується так:
![]()
![]() .
(1)
.
(1)
Відповідно
використання оптимальної змішаної
стратегії гравцем В має за будь-яких
стратегій гравця А забезпечувати програш
В, що не перевищує ціни гри
![]() :
:
![]()
![]() .
(2)
.
(2)
Ці два співвідношення застосовують для знаходження розв’язку гри.
Отже,
потрібно знайти
![]() ,
щоб
,
щоб
![]()
за умов
![]() ,
,
![]() ,
,
![]() .
.
Зауважимо, що ціна гри невідома і має бути визначена під час розв’язування задачі.
Модель ігрової задачі може бути спрощена.
З (1) маємо:

Поділивши всі обмеження на , дістанемо:
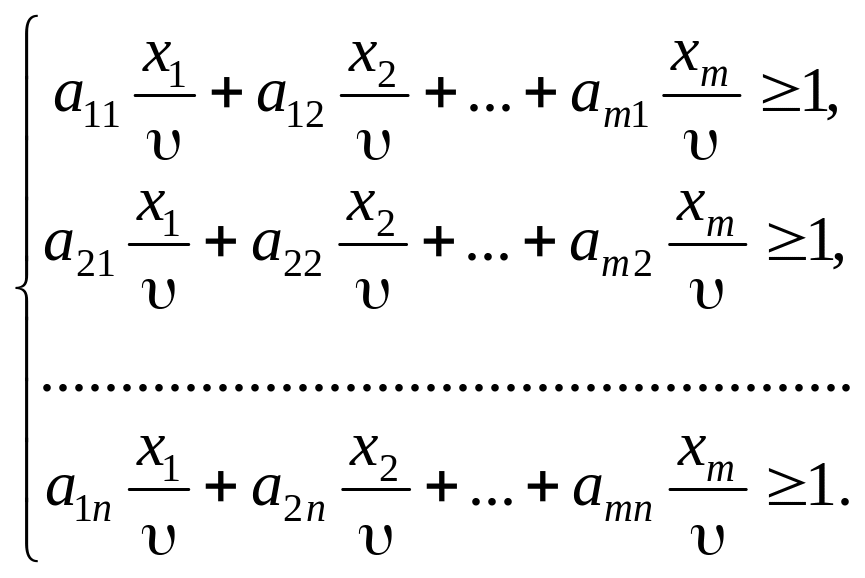
Нехай
![]() ,
тоді
,
тоді
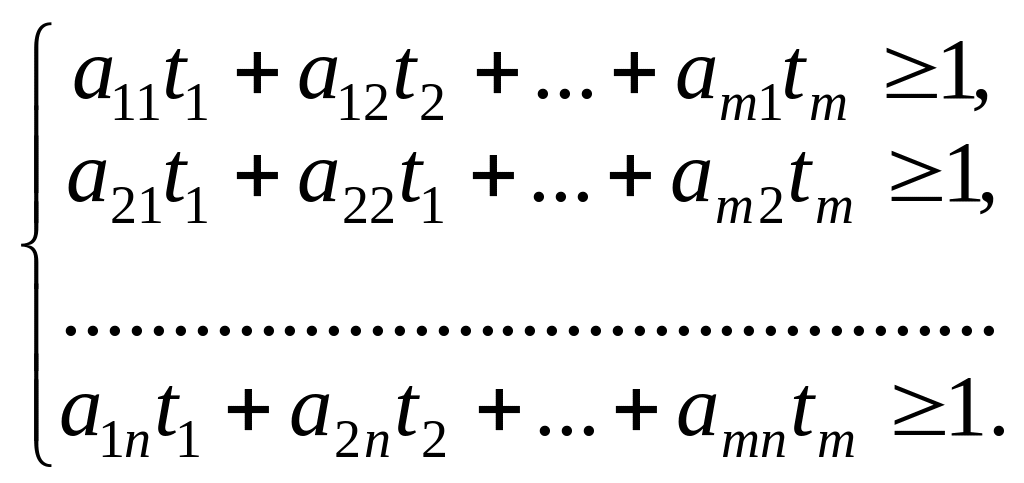
Згідно
з умовою
![]() ,
звідки
,
звідки
![]() .
.
Отже, цільова функція початкової задачі набирає такого вигляду:
![]() .
.
У результаті задача лінійного програмування:
![]() (3)
(3)
за умов
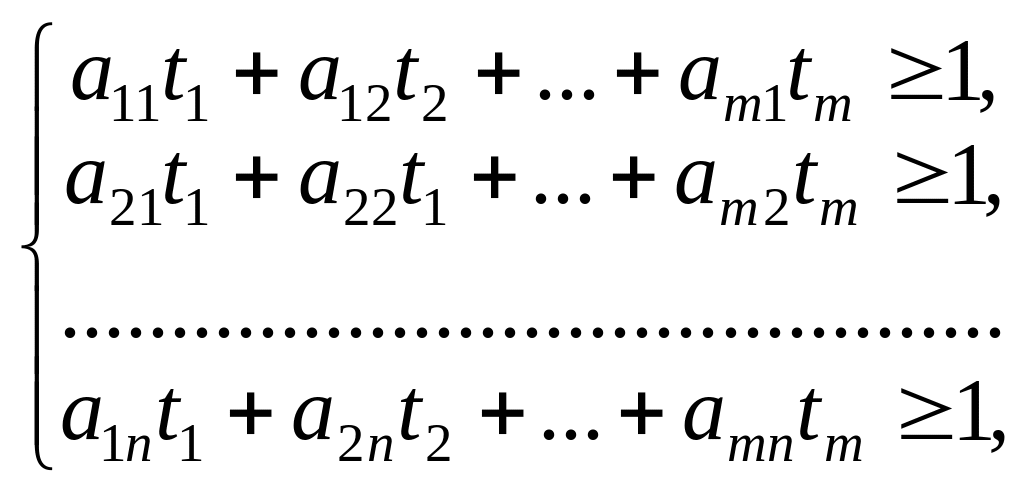 (4)
(4)
![]() . (5)
. (5)
Розв’язавши
цю задачу симплексним методом, знайдемо
значення
![]() ,
а також
,
а також
![]() і
і
![]() ,
тобто визначимо змішану оптимальну
стратегію для гравця А.
,
тобто визначимо змішану оптимальну
стратегію для гравця А.
За аналогією запишемо задачу лінійного програмування для визначення оптимальної стратегії гравця В. Нехай
![]() .
.
Тоді маємо таку лінійну модель:
![]()
за умов
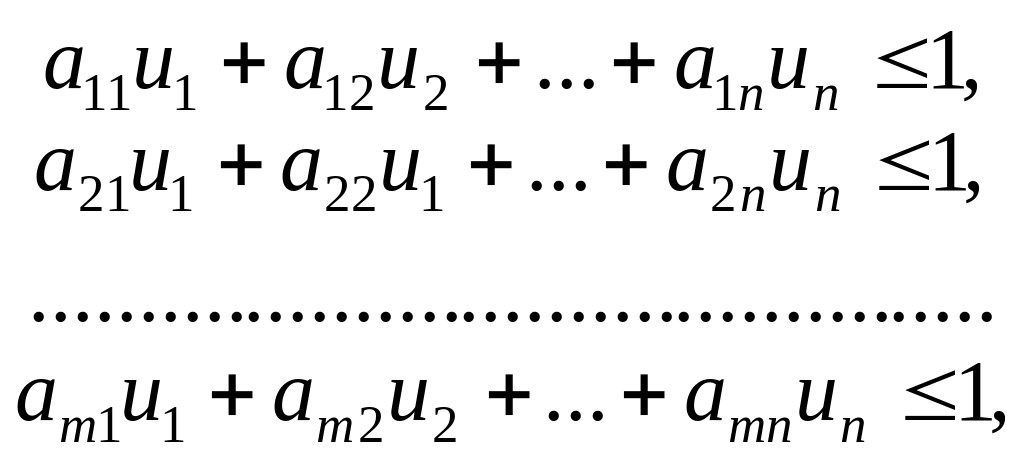
![]() .
.
Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв’язок однієї з них визначає оптимальний розв’язок спряженої.
Розглянемо приклад на застосування методів лінійного програмування до знаходження оптимального розв’язку гри.
