МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники,
электроники и автоматики"
МГТУ МИРЭА
Факультет Информационных технологий
(наименование кафедры)
Утверждаю
Заведующий
кафедрой ______________________
« » _____________ 2012г.
ЗАДАНИЕ
на выполнение курсовой работы
по дисциплине «Дискретная математика»
Студент Полинко Сергей Дмитриевич Группа ИВБ-3-11
1.Тема «Курсовая работа по дискретной математике за I курс»
2. Исходные данные:
3. Перечень вопросов, подлежащих разработке, и обязательного графического материала:
1, 2, 3, 4, 5 задания сопровождаются обязательным графическим материалом.
4. Срок представления к защите курсовой работы: до « » ________ 2012г.
Задание на курсовую работу выдал « » _________2012г. Подпись руководителя
Антик М.И.
Задание на курсовую работу получил « » _________2012г. Подпись исполнителя
Полинко С.Д.
№1. Выяснить взаимное расположение множеств D, E, F, если A, B, C –произвольные подмножества U. Указать расположение множеств на карте Карно. Для каждого множества написать минимальную дизьюнктивную формулу.
D: B Δ C + ( A * ( C \ B ) )
E: B + C
F: ( B * C ) + ( ( A \ C ) \ B )
B Δ C ( A * ( C \ B ) )
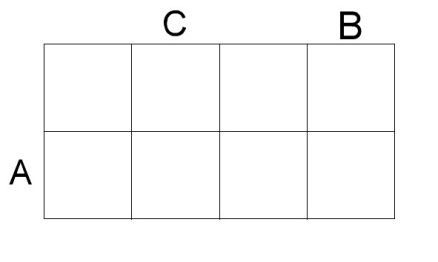
B Δ C + ( A * ( C \ B ) )
B C
B + C
B * C ( A \ C ) \ B
B * C + ( A \ C ) \ B
F D E
Минимизированные:
D: ( B \ C ) * ( ( C \ B ) \ A)
E: B + C
F: ( B * C ) + ( A * B * C )
№2. Проверить, что для любых множеств A, B, C выполнение включения α влечет выполнение включения β.
α : B \ C A
β : B C + ( B * A )
α : ( b * c ) + a = b +1 c +2 a
β : b +5 c +4 ( b *3 a )
a |
b |
c |
1 |
2 |
3 |
4 |
5 |
α |
β |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
α < = > β
№3. Для произвольных множеств A, B, H проверить, является ли выполнение включения α необходимым и достаточным условием выполнения равенства β.
A + B α H H \ A =β ( A Δ H ) + ( B \ A )
α: a + b + h β: ( h * a ) = ( ( h * a ) + ( b * a ) ) + ( b * a )
( a *1 b ) +2 h ( h *3 a ) =9 ( ( h *4 a ) +6 ( a *5 b ) ) +8 ( b *7 a )
a |
b |
h |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
α |
β |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
β -> α , является.
№4. Выяснить, верно ли равенство α для произвольных A, B, C.
α : B * ( A \ C ) = ( B * ( A + C ) ) * ( B * C )
α : b *2 ( a *1 c ) = ( b *4 ( a +3 c ) ) *6 ( b *5 c )
a |
b |
c |
1 |
2 |
3 |
4 |
5 |
6 |
2 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
2 < > 6 => для произвольных A, B и C равенство α не верно
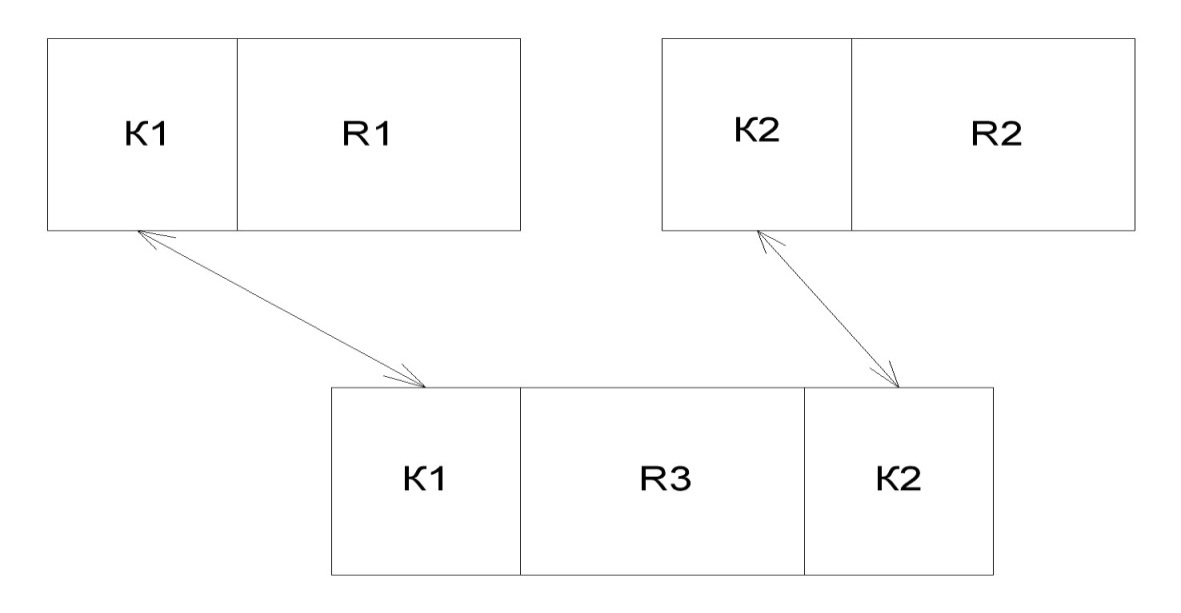
Террористический акт |
Кол-во пострадавших |
Место терр. акта |
Ф.И.О. террористов |
Код уголовного дела*к2 |
Террорист |
Ф.И.О.*к1 |
Возраст |
Происхождение |
