8.3. Знакопеременные ряды

Определение 5. Числовой ряд называется знакопеременным, если его члены могут иметь как положительные, так и отрицательные знаки. Например, .

Теорема 9. (Достаточный признак сходимости) Если сходится ряд , то сходится и ряд .

□ По критерию Коши, из сходимости следует:

, но справедливо неравенство

, т.е. выполняется критерий Коши для ряда и он сходится. ■

Пример 8. Знакопеременный ряд сходится, т.к. сходится обобщенный гармонический ряд с показателем равным двум.

Определение 6. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов.

Из теоремы 9 ясно, что всякий абсолютно сходящийся ряд является просто сходящимся.

Определение 7. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 9. Знакопеременный ряд сходится абсолютно, т.к. , а ряд сходится.

Среди знакопеременных рядов очень важное место занимают знакочередующиеся ряды, т.е. ряды вида:

, (17)

где .

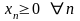Такой ряд иногда называют рядом Лейбница. Для этих рядов справедлив достаточный признак.

Теорема 10. (Признак Лейбница) Пусть члены знакочередующегося ряда (17) монотонно убывают, т.е. , тогда ряд сходится.

□ Обозначим через последовательность частичных сумм. Рассмотрим две ее подпоследовательности и , m=1,2,3, . . .

Последовательность не убывает, т.к. , т.к. .

Последовательность не возрастает, т.к. .

Последовательность ограничена сверху. Действительно, Т.е. подпоследовательность монотонная (не убывает) и ограничена сверху, следовательно, она имеет предел (конечный). Обозначим

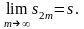
Но , тогда .

Следовательно, четные и нечетные суммы имеют один предел s. Тогда

и ряд по определению сходится. ■

Следствие. Абсолютная погрешность при замене суммы знакочередующегося ряда его частичной суммой не превосходит первого отброшенного члена ряда, т.е.

□ Т.к. не возрастают и стремятся к s, а - не убывают и стремятся к s, то .Тогда

_{то есть}

■

Замечание . Теорема остается верной, если условие выполняется, начиная с некоторого N.

Следствие играет большую роль в практических вычислениях с помощью рядов.

Пример10. Вычислить с точностью δ=0,001 сумму ряда

.

Так как , то сумма будет приближенно равна

Теперь будем рассматривать произвольные знакопеременные ряды.

Теорема 11. (Признак Дирихле) Пусть дан , такой, что последовательность монотонно стремится к 0, а последовательность частичных сумм ряда ограничена, тогда ряд сходится.

□ Вначале отметим, что имеет место неравенство Абеля при условиях данной теоремы

, (18)

где М константа, ограничивающая последовательность частичных сумм , т.е. , т.е.

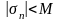
Перейдем к доказательству. В силу ограниченности последовательности имеем

Проверим критерий Коши. Возьмем произвольное число ε>0. Т.к.

.

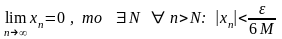Теперь применим неравенство Абеля к сумме , где n>N

, т.е. для ряда выполняется признак Коши, а, следовательно, он сходится. ■

Пример 11. Исследовать сходимость ряда .

Пусть α≠2πm Тогда

Тогда

Если α=2πm, то все слагаемые равны нулю и сумма равна нулю. Т.о. частичные суммы ограничены. Последовательность монотонно убывает и , следовательно, по признаку Дирихле ряд сходится.

Замечание. Очевидно, признак Лейбница есть частный случай признака Дирихле при .

Теорема 12. (Признак Абеля) Если последовательность монотонна и ограничена, а ряд сходится, то сходится и ряд .

□ В силу ограниченности последовательности и сходимости ряда следует по критерию Коши

Тогда и всех целых используя неравенство Абеля (18) имеем

По критерию Коши ряд сходится. □

Пример 12. Исследовать сходимость ряда .

Ряд сходится по признаку Дирихле, т.к. последовательность частичных сумм ряда ограничена, а монотонно. Последовательность монотонна. Отсюда следует, что ряд сходится.

Следующие две теоремы показывают существенное различие между абсолютно и условно сходящимися рядами.

Теорема 13. (Риман) Если ряд знакопеременный ряд сходится условно и s произвольное вещественное число, то можно так переставить члены этого ряда, что полученный ряд будет иметь сумму равную s. (Без доказательства)

Пример 13. Ряд сходится условно. Пусть его сумма s. Сгруппируем слагаемые так: один положительный, затем два отрицательных, один положительный, затем два отрицательных и т.д., и найдем сумму

т.е. сумма изменилась, следовательно, переставлять слагаемые в условно сходящемся ряде нельзя.

Теорема 14 . Если знакопеременный числовой ряд сходится абсолютно, то новый ряд, полученный перестановкой его членов, также сходится абсолютно и имеет ту же сумму. (Без доказательства)

12.7.Контрольные вопросы

26. Какое выражение называется числовым рядом? Что называется общим членом ряда?

27. Как определяется -я частичная сумма ряда?

28. Что называется суммой ряда? Какие ряды называются сходящимися и расходящимися?

29. При каких условиях ряд бесконечной геометрической прогрессии сходится, а при каких расходится?

30. Сформулируйте основные свойства сходящихся рядов.

31. В чем состоит необходимый признак сходимости и необходимый признак расходимости ряда?

32. Сформулируйте основные достаточные признаки сходимости знакоположительных рядов: признак сравнения, признак Даламбера, радикальный признак Коши и признак разреженности.

33. Укажите условия сходимости и расходимости обобщенного гармонического ряда.

34. Какой ряд называется знакочередующимся? Сформулируйте признак Лейбница.

35. Какой ряд называется знакопеременным? Сформулируйте достаточный признак сходимости знакопеременного ряда.

36. В чем состоит отличие абсолютной и условной сходимости знакопеременного ряда?

37. Сформулируйте основные свойства знакопеременных рядов.