Глава 8. Числовые ряды
8.1. Основные понятия
Пусть
=
- числовая последовательность.
Определение 1. Выражение вида (формально составленная сумма)
(1)
называется
числовым
рядом, а
- его к-м
членом.
Другими
словами, ряд есть бесконечная сумма
членов некоторой числовой последовательности.
Сумма первых n
членов числовой последовательности
называется частичной
суммой ряда
и обозначается
:
.
Числовая
последовательность
называется последовательностью
частичных сумм.
Определение 2. Числовой ряд называется сходящимся, если сходится последовательности его частичных сумм .
Предел
последовательности
,
равный
,
называют суммой
ряда:
.
В
этом случае пишут
.
Если последовательность
расходится, то говорят, что и числовой
ряд расходится. Можно записать
.
Величина
называется остатком
ряда.
Замечание.
По определению
2 сходимость ряда (1) равносильна сходимости
числовой последовательности
.
Наоборот, если
- некоторая числовая последовательность,
то вопрос о ее сходимости равносилен
сходимости ряда
,
,
для которого частичными суммами будут
как раз члены последовательности
.
Это иногда используют для доказательства
сходимости рядов и последовательностей.
Таким образом, числовые ряды есть новая форма изучения числовых последовательностей.
Одна из главных задач теории числовых рядов состоит в изучении вопроса о сходимости и расходимости.
Пример
1. а) Исследовать
сходимость ряда
Рассмотрим
последовательность частичных сумм:
,
,
,
,….,
,
,…
т.е.
.
Эта последовательность не имеет предела, поэтому ряд расходится.
б)
Исследовать сходимость ряда
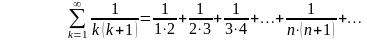
Составим последовательность частичных сумм . Так как
,
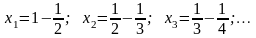
то
.
,
откуда следует, что ряд сходится.
Аналогичным
образом найти сумму ряда
,
где
в)
Исследовать сходимость ряда в зависимости
от параметра q
:
Частичной суммой ряда является сумма геометрической прогрессии:
.
.
Если
,
не существует и ряд расходится;
если
- ряд расходится;
если
расходится (см. пример 1):
если
=
, т.к.
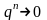и ряд сходится.
г)
Показать, что ряд
расходится.
Так
как частичную сумму
можно записать как
,
то
при
и ряд расходится.
Пусть
и
- два числовых ряда.
Определение 3. Суммой и разностью этих рядов, а также произведением ряда на число называют следующие ряды:
;
.
Теорема
1. Если ряды
и
сходятся, то сходится их сумма, разность
и произведение на число, причем
;
□
Пусть
,
- частичные суммы заданных рядов, а
- частичная сумма ряда
.
Т.к.
- конечная сумма, то слагаемые в ней
можно переставлять, т.е.
.
Откуда
Аналогично доказывается для
и
.
■
Замечание. Отбрасывание или добавление конечного числа слагаемых к членам ряда не влияет на его сходимость или расходимость, т.к. в этом случае его частичная сумма изменится на постоянное число.
Теорема
2. (Критерий
Коши) Для сходимости ряда
необходимо и достаточно, чтобы
(2)
Очевидно, что неравенство (2) равносильно следующему:
(3)
□ По определению сходимость ряда (1) равносильна сходимости последовательности , поэтому условие сходимости ряда совпадает с условием сходимости числовой последовательности .
Необходимым
и достаточным условием сходимости
последовательности является критерий
Коши:
.
Обозначим
,
тогда
.
■
Следствие.
(Необходимое условие сходимости ряда)
Если ряд (1) сходится, то
□ При
получим, согласно критерия Коши, что
,
т.е.
,
т.е.
.
■
Отметим, что это условие необходимое, но не достаточное, т.е. если предел равен нулю, то ряд может сходиться, а может и расходиться.
Пример
2. Рассмотрим
ряд
,
который называется гармоническим
рядом.
Очевидно,
что
.
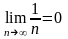Докажем, что ряд расходится. Воспользуемся
критерием Коши. Возьмем
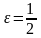и
.
Тогда
.
Т.е. критерий Коши не выполняется и ряд расходится.