7.6. Частные производные и дифференциалы высших порядков. Формула Тейлора

Пусть имеет в некоторой окрестности точки все частные производные первого порядка , , . Эти частные производные сами являются функциями n переменных в . Тогда они могут иметь частные производные, т.е. в точке можно определить следующие величины

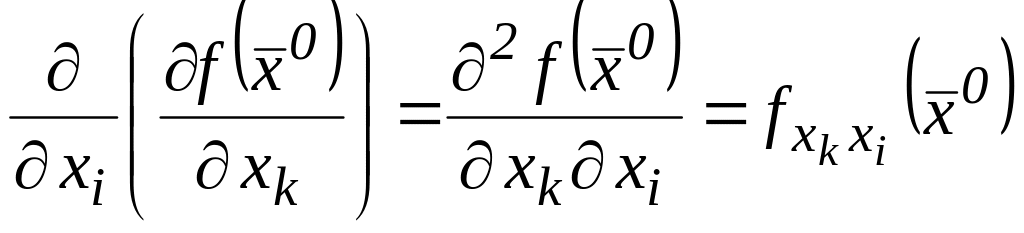, , (24)

которые называют частными производными второго порядка или вторыми частными производными.

Если , то соотношения (24) задают так называемые смешанные частные производные. Например, для функции двух переменных существует четыре частных производных второго порядка:

.

Пример 19. Найти все частные производные второго порядка для функции .

Решение. ,

,

,

.

Имеют место следующие две теоремы о равенстве смешанных производных функции .

Теорема 9. (К.Г.Шварц 1848-1921 нем.). Пусть функция в некоторой окрестности точки имеет смешанные производные второго порядка и , причем они непрерывны в точке . Тогда в точке эти частные производные равны между собой

.

Без доказательства.

Теорема 10. (У.Г.Юнг 1863-1942 англ.). Пусть функции и определены в некоторой окрестности точки и дифференцируемы в этой точке. Тогда вторые смешанные частные производные не зависят от порядка дифференцирования

. (25)

 Доказательство проведем для случая функции двух переменных . Пусть точка, в которой вычисляются производные. Докажем справедливость равенства . Рассмотрим функцию в окрестности точки , такую что

.

Обозначим

.

Тогда . Так как имеет частные производные первого порядка в , то дифференцируема по , и, следовательно, к можно в окрестности применить формулу конечных приращений Лагранжа.

(26)

.

Так как производные и дифференцируемы в точке , то приращения в квадратных скобках (26) можно также записать по формуле Лагранжа

,

где и при , т.е. .

Аналогично, получаем

,

где при .

Подставим это выражение в (26):

,

где .

Аналогично, если представить , где , то можно получить

,

где и .

Тогда, приравнивая , будем иметь:

,

а переходя к пределу при получим (25). 

Теоремы Шварца и Юнга справедливы и при n>2.

Определение 20. Функция называется дважды дифференцируемой в точке, если все первые частные производные дифференцируемы в этой точке.

В общем случае, называют n-раз дифференцируемой, если все ее частные производные (n-1)-го порядка являются дифференцируемыми функциями, а частная производная первого порядка от (n-1)-ой производной называется производной n-го порядка.

Можно показать, что если функция является n раз дифференцируемой, то смешанные частные производные до n-го порядка не зависят от порядка, в котором производится дифференцирование.

Пример 20. Найти функции .

Определение 21. Дифференциалом второго порядка (вторым дифференциалом) дважды дифференцируемой в некоторой окрестности точки , функции называют следующий однородный многочлен второй степени относительно переменных

. (27)

В частности, если , то

.

Так как , то выражение для дифференциала второго порядка функции двух переменных принимает вид

.

Запишем формулу (27) подробно в точке для функции n-переменных

.

Все производные вычисляются в точке , и все смешанные производные с соответственными индексами равны между собой, т.е. . Следовательно, есть квадратичная форма относительно n переменных . Матрица этой квадратичной формы, называется матрицей Гессе:

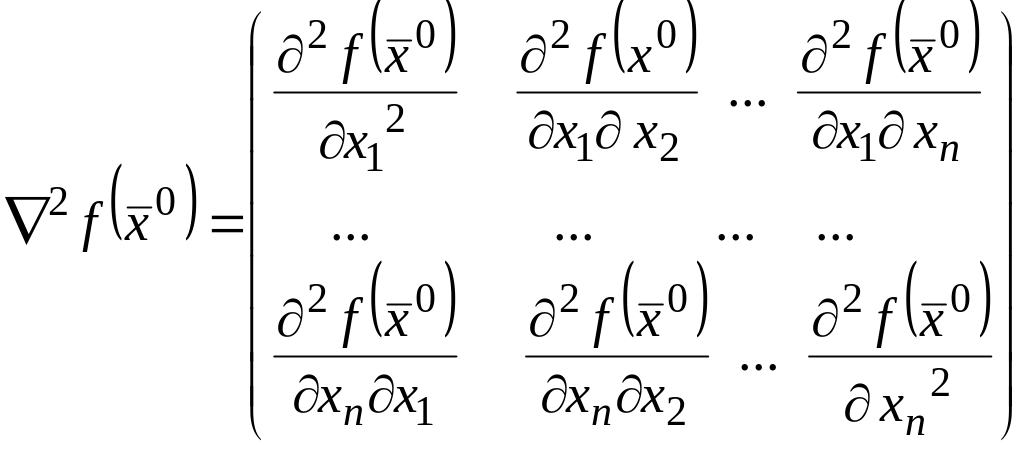. (28)

Следовательно, можно записать в матричной форме

,

где .

Определение 22. Дифференциалом m-го порядка m раз дифференцируемой функции называется однородный многочлен m-й степени относительно переменных вида

.

Это выражение символически можно записать так

,

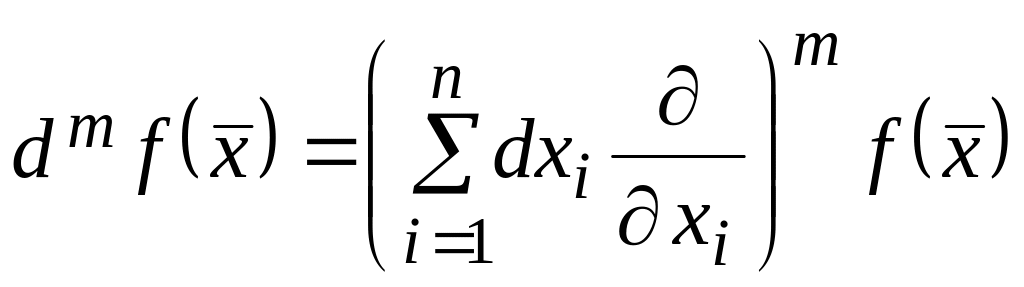где для получения развернутого выражения надо формально возвести выражение в скобках в m-ю степень, как многочлен, считая символы независимыми переменными, а затем к числителю приписать справа . В частности, для функции двух переменных имеем

.

Так как , то получаем:

,

где – биномиальные коэффициенты.

Дифференциалы порядка не обладают свойством инвариантности.

Теорема 11. (Тейлор Брук 1685-1731 англ.). Пусть функция определена в некоторой -окрестности точки и (m+1) раз дифференцируема в этой окрестности. Тогда справедлива формула Тейлора

(29)

Здесь некоторая точка из окрестности , зависящая от , а дифференциалы независимых переменных в каждом слагаемом определяются как .