
- •Московский государственный институт индустрии туризма
- •080502.65 Экономика и управление на предприятии (туризм и
- •100201.65 Туризм
- •Дифференциальное исчисление функции одной переменной Теоретические вопросы
- •Контрольная работа
- •Исследование функции методами дифференциального исчисления и построение её графика Теоретические вопросы
- •Расчётная работа № 4 Задачи для самостоятельного решения
- •Неопределённый и определённый интегралы Теоретические вопросы
- •Расчётная работа № 5 Примеры для самостоятельного решения
- •Часть 1
- •Решение типовых примеров.
- •Задачи для самостоятельного решения
- •Часть II
- •Решение типовых примеров
- •Тема 1. Дифференциальное исчисление функции одной переменной……………3
- •Тема 2. Неопределённый и определённый интегралы………………… …………19
Неопределённый и определённый интегралы Теоретические вопросы
1. Что называется первообразной функцией?
2. Что называется неопределённым интегралом?
3. Перечислите основные свойства неопределённого интеграла.
4. Каков геометрический смысл неопределённого интеграла?
5. Что понимают под непосредственным интегрированием?
6. В чём состоит способ подстановки?
7. Напишите формулу интегрирования по частям.
8. Каковы основные приёмы интегрирования рациональных дробей?
9. Какие задачи приводят к понятию определённого интеграла?
10. Что называется интегральной суммой функции f (х) на интервале [а; в] ?
11. Что называется определённым интегралом; в чём его геометрический смысл?
12. Перечислите основные свойства определённого интеграла.
13. Напишите формулу Ньютона – Лейбница.
14. В чём состоит способ подстановки в определённом интеграле?
15. Напишите формулу интегрирования по частям в определённом интеграле.
16. С помощью каких формул можно вычислить определённый интеграл приближенно?
17. С помощью каких формул можно вычислить площади плоских фигур и объёмы тел
вращения?
18. Что называется несобственным интегралом? Вычисление несобственных интегралов.
Таблица основных интегралов
1.

![]() 8.
8.
![]()
2.
![]() 9.
9.

3.
 10.
10.
![]()
4.
![]() 11.
11.

5.
![]() 12.
12.
![]()
6.
![]() 13.
13.

7.
![]() 14.
14.

Каждая из формул этой таблицы справедлива в любом промежутке, содержащемся в области определения соответствующей подынтегральной функции.
Справедливость приведённых формул проверяется дифференцированием.
Расчётная работа № 5 Примеры для самостоятельного решения
Часть 1
Найти неопределённые интегралы и результаты интегрирования проверить дифференцированием.
1. a)
 б)
б)
![]()
в)
![]() г)
г)

2. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
3. а)
![]() б)
б)

в)
![]() г)
г)

4. а)
![]() б)
б)

в)
![]() г)
г)
![]()
5. а)
![]() б)
б)

в)
![]() г)
г)
![]()
6. а)
![]() б)
б)
![]()
в)
![]() г)
г)

7. а)
 б)
б)
![]()
в)
![]() г)
г)
![]()
8. а)
![]() б)
б)
![]()
в)
![]() г)
г)

9. а)
![]() ,
б)
,
б)
![]()
в)
 г)
г)
![]()
10. а)
![]() б)
б)
![]()
в)
 г)
г)

11. а)
![]() б)
б)
![]()
в)
![]() г)
г)

12. а)
![]() б)
б)

в)
![]() г)
г)
![]()
13. а)
![]() б)
б)
![]()
в)
![]() г)
г)

14. а)
 б)
б)
![]()
в)
![]() г)
г)

15. а)
![]() б)
б)
![]()
в)
![]() г)
г)
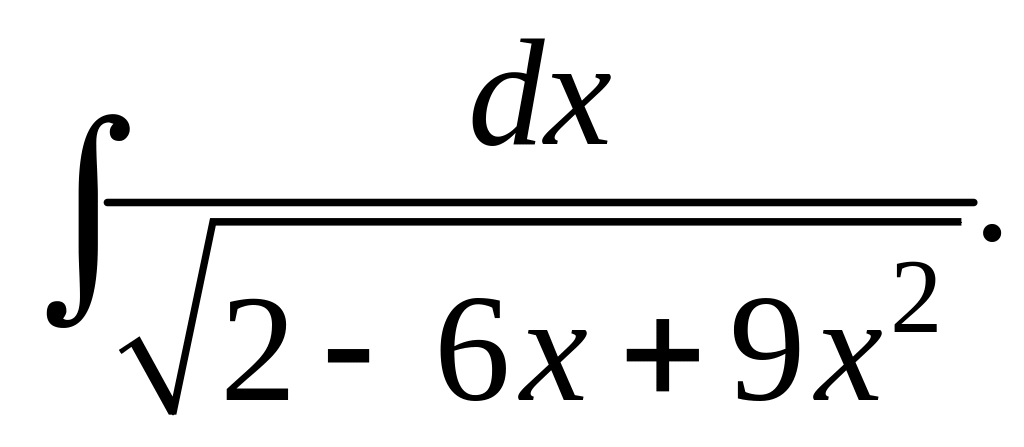
16. а)
 б)
б)
![]()
в)
 г)
г)

17. а)
![]() б)
б)
![]()
в)
![]() ,
г)
,
г)
![]()
18. а)
 б)
б)
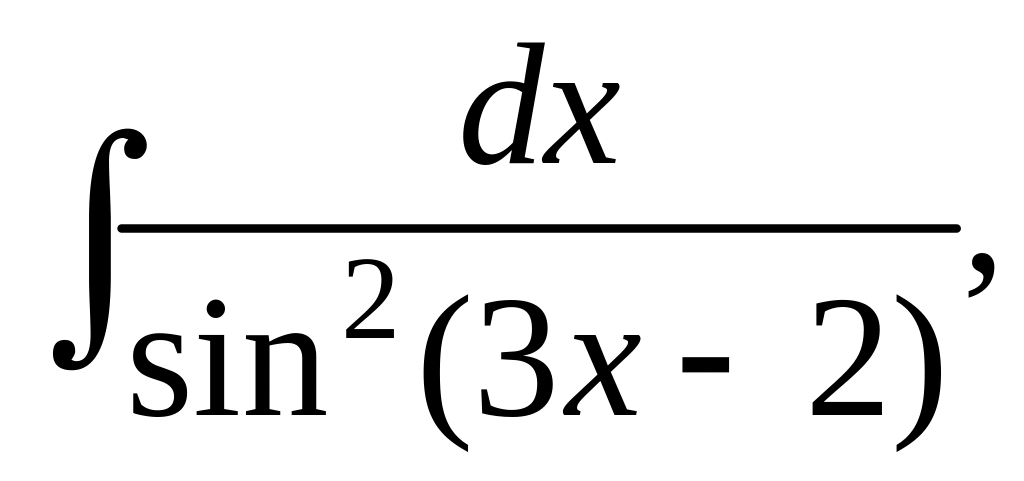
в)
![]() г)
г)
![]()
19. а)
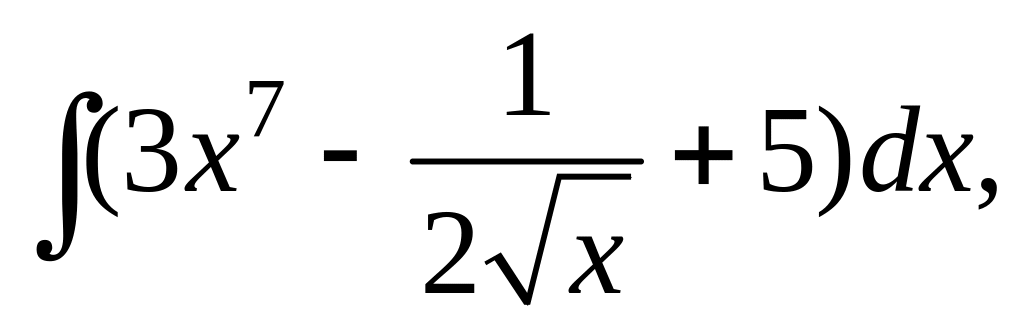 б)
б)
![]()
в)
 г)
г)
![]()
20. а)
 б)
б)
![]()
в)
![]() г)
г)

