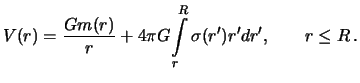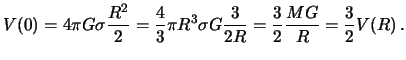3.3.1 Потенциал шара во внутренней точке

Рассмотрим сначала бесконечно тонкий шаровой слой с внутренней полостью, не содержащей массы. Тогда можно доказать, что внутри этой полости потенциал (силовая функция) есть постоянная величина, то есть этот шаровой слой внутреннюю точку не притягивает. Обратимся к рисунку. Через точку проведем коническую поверхность с вершиной в этой точке. Тогда эта поверхность вырежет на сферической поверхности элементарную площадку , а на другой стороне сферы -- элементарную площадку . Точка лежит под площадкой на расстоянии и испытывает со стороны этой площадки притяжение, равное , где -- коэффициент пропорциональности, зависящий от поверхностной плотности этого шара и от направления внешней нормали к площадке по отношению к радиусу-вектору точки . Элементарная площадка расположена на расстоянии от точки . Поскольку обе площадки видны из точки под одним и тем же телесным углом, то

Итак, обе силы равны и направлены в противоположные стороны. Теперь будем рассуждать следующим образом. Через точку Р проведем плоскость перпендикулярную радиус-вектору этой точки. Она разделит сферический "пузырь" на две части, назовем их условно верхнюю и нижнюю. Поскольку каждую из частей можно представить как бесконечную сумму элементарных площадок, то для каждой элементарной площадки верхней полусферы найдется симметричная ей площадка в нижней полусфере. Силы притяжения материальной точки, помещенной в точку , со стороны верхней и нижней полусфер равны и противоположны по направлению. Отсюда вывод: материальная точка, помещенная внутри полой сферы, этой сферой не притягивается

Рассуждения, приведенные здесь, нельзя считать строго математически обоснованными. Мы рассчитываем больше на интуицию, чем на строгую математическую логику. Однако, в теории потенциала притяжения математически строго доказано, что оболочка не притягивает материальную точку и в случае, когда эта оболочка имеет эллипсоидальную форму.

Мы показали, что гравитационный потенциал в полости, окруженной сферической поверхностью, является постоянной величиной. Однако, это имеет место лишь в том случае, когда эта полость притягивающих масс не содержит. Теперь откажемся от этого условия, и будем считать, что шар не полый, но плотность зависит только от расстояния до центра шара. Проведем через точку сферу так, что она разделит шар на внутренний шар с массой и шаровой слой с массой . Материальная точка будет притягиваться только внутренним шаром, так как шаровой слой, как мы видели, внутреннюю точку не притягивает. Поэтому гравитационная сила в точке направлена в центр шара и равна .

Знак "минус" мы поставили, чтобы подчеркнуть, что сила направлена в сторону, противоположную радиус-вектору. Массу внутреннего шара можно получить, интегрируя массу бесконечно тонкой сферы в пределах от 0 до

(3.8)

Поскольку , то для гравитационного потенциала во внутренней точке шара получим

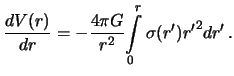
Интегрируя, будем иметь

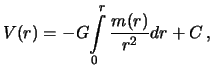
где С -- постоянная интегрирования. Полученное выражение можно проинтегрировать по частям. . Согласно формуле (3.8) : , поэтому 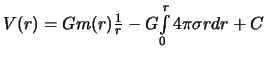. Определим теперь постоянную . Мы знаем, что , поэтому 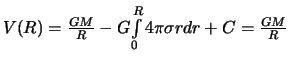. Следовательно .

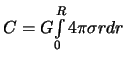Окончательно, формула для гравитационного потенциала во внутренней точке шара со сферически симметричной распределенной массой принимает вид

(3.9)

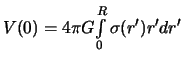При переходе через поверхность потенциал сохраняет непрерывность. Очевидно, что при , будем иметь -- потенциал точки с массой, равной , расположенной в центре шара. В случае, когда точка находится в центре шара, то есть при , , а , то эта величина зависит от закона изменения плотности с глубиной. В частности, если шар -- однородный, то его потенциал в центре шара равен

(3.10)

Отсюда следует вывод, что гравитационный потенциал в центре однородного шара в полтора раза больше, чем на его поверхности.