ВВЕДЕНИЕ

Работа составлена на основе лекций по дискретной математике, читаемых в течение одного семестра студентам первого курса факультета бизнеса, обучающимся по специальности «Прикладная информатика в экономике». Конспект лекций содержит четыре раздела: элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов.

Целью данного курса является дать слушателям основные понятия дискретной математики, которые необходимы для дальнейшего обучения данной специальности.

Основные понятия теории множеств, которые изложены в первой главе, составляют базовый язык математики (а значит, и дискретной) и поэтому необходимы для изучения остальных разделов. Работа компьютеров основана на двоичной системе счисления и поэтому все преобразования информации осуществляются по законам алгебры логики. Известны также применения алгебры логики в теории контактных и релейно-контактных схем, при анализе алгоритмов программ, синтезе управляющих систем. Основные понятия комбинаторики необходимы для изучения курса теории вероятностей. В экономических исследованиях также нередко возникают задачи, которые решаются с использованием методов комбинаторики. Теория графов применяется для решения задач в различных областях науки и техники, в том числе и в экономике, например, для решения задач нахождения кратчайших маршрутов в транспортных сетях.

Для изучения данного курса студентам достаточно знаний математики в объеме средней школы.

I. Теория множеств

1. Понятие множества, операции над множествами

1.1. Множества и подмножества

В математике понятия множества и его элементов, так же как понятия точки, прямой, вектора, относятся к исходным понятиям и никак не определяются.

Мы будем понимать под множеством всякую совокупность каких-либо объектов. Объекты этой совокупности есть элементы данного множества. Обычно множества обозначаются прописными, а элементы множества строчными буквами.

Принадлежность элемента множеству обозначается ( принадлежит ).

Если элемент не принадлежит множеству , то, в этом случае, используется обозначение .

Пример 1

1) – множество жителей в г. Новосибирске.

2) – множество планет Солнечной системы.

3) – множество действительных чисел; .

4) – множество натуральных чисел; ; .

Множество называется подмножеством множества , если всякий элемент множества является элементом множества . При этом используется обозначение . Знак называется знаком включения. В этом случае говорят, что В содержит А.

Множества А и равны , если их элементы совпадают, т.е. если АВ и ВА. В этом случае пишут .

Обычно для доказательства равенства двух множеств и доказывают два включения АВ и ВА.

Если элементы множеств А и не совпадают, то эти множества не равны (обозначение ).

Если и , то называется строгим подмножеством . Обозначение знак  называется знаком строгого включения.

Множества могут быть конечными (состоящие из конечного числа элементов) и бесконечными.

Число элементов в конечном множестве называется мощностью и обозначается. О мощности бесконечного множества будет говориться в следующих разделах.

Множество мощности 0, т.е. не содержащее элементов, называется пустым и обозначается . Принято считать, что пустое множество является подмножеством любого множества. Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсумом и обозначается .

2. Способы задания множеств

   Обычно выделяют следующие способы задания множеств: списком своих элементов; порождающей процедурой или описанием характеристических свойств, которыми должны обладать его элементы.

Списком можно задавать лишь конечные множества. Список обычно заключают в фигурные скобки, например, означает, что множество состоит из четырех элементов .

Порождающая процедура описывает способ получения элементов множества из уже полученных элементов либо из других объектов. Элементами множества считаются все объекты, которые могут быть построены с помощью такой процедуры.

Пример 2

1) Множество есть множество решений уравнения .

2) Множество чисел Фибоначи

.

Когда используется способ задания множества путем описания свойств его элементов, то указываются свойства, которым должны удовлетворять все элементы данного множества.

Пример 3

 множество точек единичного круга на плоскости;

 множество действительных чисел, синус которых меньше

1.3. Операции над множествами

Объединением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств. Объединение обозначается .

или

Объединение множеств, принадлежащих произвольной (в том числе бесконечной) системе множеств, определяется аналогично. При этом используются следующие обозначения:

– объединение множеств А, В, С, D ;

 объединение множеств, принадлежащих системе S. Если множества, занумерованы индексами, то обычно пишут для системы, состоящей из множеств, и  для бесконечного числа множеств.

Пример 4

1) Пусть , , тогда .

2) А – множество решений уравнения :

3) Множество точек плоскости есть объединение точек правой и левой полуплоскостей

Пересечением множеств и В называется множество, состоящее из тех и только тех элементов, которые принадлежат и А и В.

Обозначение .

и .

Аналогично, как для операции объединения определяется пересечение произвольной, в том числе и бесконечной системы множеств.

Пример 5

1. Пусть , , тогда ;

2. Рассмотрим , где  круг радиуса , тогда множество содержит единственный элемент  точку .

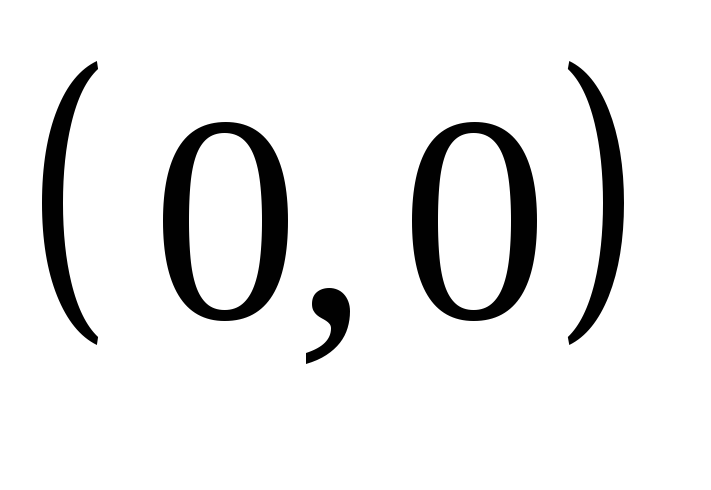Разностью множеств и называется множество всех тех и только тех элементов , которые не принадлежат . При этом используется обозначение .

В отличие от операций объединения и пересечения разность строго двуместна, т.е. определена только для двух множеств.

Пример 6

, , .

Свойства операции «разность»:

1) разность определена только для двух множеств;

2) разность некоммутативна, т.е. ;

3) если , то .

Дополнением множества называется множество всех элементов, не принадлежащих (но принадлежащих )

Пример 7

Пусть − множество точек плоскости, находящихся в круге радиуса 1, тогда – внешность единичного круга.

Симметрической разностью множеств и называется множество

.

На рис.1. изображены круги Эйлера, наглядно иллюстрирующие операции над множествами. Сами множества представлены кругами, а результаты операций выделены штриховкой.

Рис.1. Операции над множествами

1.4. Свойства операций над множествами

1. Коммутативность:

, ;

2. Ассоциативность:

, A ∩(B ∩ C) = (A ∩ B)∩C;

3. Дистрибутивность:

A∩(BUC)=(A∩B)U(A∩C), AU(B∩C)=(AUB)∩(AUC) ;

4. Идемпотентность:

AUA=A, A∩A=A;

5. Поглощение:

, ;

5. Свойства нуля:

, ;

5. Свойства единицы:

, ;

5. Инволютивность:

;

9. Законы де Моргана:

, ;

5. Свойства дополнения:

, .

1.5. Разбиения и покрытия

Пусть  некоторое семейство подмножеств множества , . Семейство называется покрытием множества , если каждый элемент принадлежит хотя бы одному из множеств .

Покрытие называется разбиением множества , если для любых двух множеств выполняется , .

Пример 8

Пусть и  два множества, имеющие не пустое пересечение. Рассмотрим . Тогда семейство является покрытием множества . Семейство является разбиением множества .