Пример 6
1.
Обычное отношение «» на множествах
и
является частичным порядком.
2.
Отношение делимости на
.
Для
любого множества
отношение
«
»
является частичным порядком на множестве
всех подмножеств
.
Отношение,
обратное к частичному порядку «»,
является частичным порядком, который
называется двойственным
к
«» и обозначается «». Таким образом,
,
тогда и только тогда, когда
.
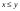Если
и
,
то используется обозначение
.
Частично упорядоченные множества, состоящие из небольшого количества элементов, удобно описывать диаграммами. Кружочками обозначаются элементы; линия, идущая вверх, соединяет элемент с каждым непосредственно следующим за ним большим элементом.
Пример 7
Рассмотрим
множество
и множество его подмножеств, частично
упорядоченное относительно отношения
включения. На рис. 1.2 приведена
соответствующая диаграмма.
Рис. 1.2. Частичный порядок на множестве
подмножеств
Частичный
порядок “” на множестве
называется линейным,
если для любых двух элементов
выполняется
или
.
Множество
с заданным на нем частичным (линейным)
порядком называется частично
(линейно) упорядоченным.
Элемент
а
частично упорядоченного множества
называется максимальным,
если из того, что
,
следует
.
Элемент
а
частично упорядоченного множества
называется минимальным,
если из того, что
,
следует
.
Пример 8
1.
В примере 7 с множеством подмножеств
– максимальный элемент, – минимальный.
2.
Рассмотрим
и
отношение
,
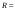
R
– есть частичный порядок,
1
– минимальный элемент, 4, 5, 6 – максимальные
элементы.
3.
Пусть A =
,
рассмотрим отношение
четные
и
,
которое является частичным порядком
на
.
В этом случае существуют два минимальных
элемента на
1 и 2.
Элемент
называется наибольшим
если
для всех
.
Элемент
называется наименьшим
если
для всех
.
Пример 9
1. Рассмотрим множество подмножеств {1,2,3}. Пусть R- отношение включения. Тогда минимальный элемент равен наименьшему = , максимальный элемент равен наибольшему ={1,2,3}.
2.
Пусть
и
,
в этом случае не существует наименьшего
и наибольшего элемента.
3.
Пусть
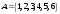и
,
тогда 1 – наименьший элемент; 6 – не
является наибольшим элементом, так как
отношение
определено не для всех элементов
.