
- •Введение
- •I. Теория множеств
- •1. Понятие множества, операции над множествами
- •1.1. Множества и подмножества
- •1.3. Операции над множествами
- •1.4. Свойства операций над множествами
- •1.5. Разбиения и покрытия
- •Пример 8
- •2. Прямое произведение множеств
- •3. Отношения и функции
- •Пример 1
- •Пример 2
- •Пример 3
- •Пример 15
- •4. Взаимно однозначные соответствия и мощности множеств
- •5. Специальные бинарные отношения
- •Пример 2
- •Пример 3
- •Пример 4
- •Пример 5
- •Пример 6
- •Пример 8
- •Пример 9
5. Специальные бинарные отношения
Мы
будем рассматривать бинарные отношения,
заданные на непустом множестве
 .
.
Бинарное
отношение R на множестве
 называется рефлексивным,
если
называется рефлексивным,
если
 для всех
для всех
 .
Если бинарное отношение рефлексивно и
.
Если бинарное отношение рефлексивно и
 конечное множество, то главная диагональ
матричного представления содержит
только единицы.
конечное множество, то главная диагональ
матричного представления содержит
только единицы.
Бинарное
отношение R на множестве А
называется антирефлексивным,
если для всех

 .
В матричном представлении главная
диагональ антирефлексивного бинарного
отношения содержит только нули.
.
В матричном представлении главная
диагональ антирефлексивного бинарного
отношения содержит только нули.
Пример 1
1.
Отношение «» на множествах
 и
и
 рефлексивно, а отношение «<»
антирефлексивно.
рефлексивно, а отношение «<»
антирефлексивно.
2.
Отношение «иметь общий делитель» на
множестве
 рефлексивно.
рефлексивно.
3. Отношение «быть симметричным относительно оси х» не является ни рефлексивным ни антирефлексивным.
Бинарное
отношение называется симметричным,
если
 .
То есть для любой пары отношение
выполняется в обе стороны либо не
выполняется вообще. Матрица симметричного
отношения симметрична относительно
главной диагонали.
.
То есть для любой пары отношение
выполняется в обе стороны либо не
выполняется вообще. Матрица симметричного
отношения симметрична относительно
главной диагонали.
Отношение
R называется антисимметричным,
если из
 и
и
 следует x
=
y.
следует x
=
y.
Пример 2
1.
Отношение « »
является симметричным.
»
является симметричным.
2.
Отношение на множестве
 «иметь общий делитель 1» является
симметричным.
«иметь общий делитель 1» является
симметричным.
3. Отношение «» является антисимметричным.
Бинарное
отношение называется транзитивным,
если
 и
и

 .
.
Пример 3
1.
Отношение «=» на
 является транзитивным:
является транзитивным:
 и
и


 .
.
2.
Отношение «» на
 является транзитивным.
является транзитивным.
3.
Отношение включения для множеств
транзитивно:
 и
и

 .
.
4.
Отношение « »
не транзитивно: из
»
не транзитивно: из
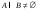 и
и
 не следует
не следует
 .
.
Бинарное отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 4
1.
Отношение равенства на
 есть отношение эквивалент-ности.
есть отношение эквивалент-ности.
2. Отношение подобия треугольников есть эквивалентность.
3.
Отношение «иметь один и тот же остаток
от деления на какое-либо число» является
эквивалентностью на
 .
.
Пусть
на множестве
 задано отношение эквивалентности R.
Тогда можно разбить множество
задано отношение эквивалентности R.
Тогда можно разбить множество
 на классы эквивалентных элементов.
Действительно, возьмем произвольный
элемент
на классы эквивалентных элементов.
Действительно, возьмем произвольный
элемент
 и образуем класс
и образуем класс
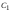 ,
состоящий из
,
состоящий из
 и всех элементов, эквивалентных
и всех элементов, эквивалентных
 .
Затем выберем
.
Затем выберем
 (если такой найдется) и образуем класс
(если такой найдется) и образуем класс
 ,
состоящий из
,
состоящий из
 и всех элементов, эквивалентных
и всех элементов, эквивалентных
 и т.д. Получается система классов
и т.д. Получается система классов
 (возможно бесконечная) такая, что любой
элемент из А
входит хотя бы в один класс, т.е.
(возможно бесконечная) такая, что любой
элемент из А
входит хотя бы в один класс, т.е.
 .
.
Эта система классов обладает следующими легко проверяемыми свойствами:
1)
система образует разбиение
 ,
такое, что классы попарно не пересекаются;
,
такое, что классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов неэквивалентны.
Построенное
разбиение, т.е. система классов называется
системой
классов эквивалентности
по отношению к R
или фактор-множеством
 по R.
Мощность этой системы называется
индексом
разбиения.
по R.
Мощность этой системы называется
индексом
разбиения.
С
другой стороны, любое разбиение
 на классы определяет некоторое отношение
эквивалентности, а именно, отношение
«входить в один и тот же класс данного
разбиения».
на классы определяет некоторое отношение
эквивалентности, а именно, отношение
«входить в один и тот же класс данного
разбиения».
Пример 5
1.
Все классы эквивалентности
 по отношению равенства состоят из одного
элемента.
по отношению равенства состоят из одного
элемента.
2. Разбиение множества треугольников на классы эквивалентности по отношению подобия.
3. Разбиение N по отношению «иметь общий остаток от деления на 3»:
 ,
,
 ,
,
 .
.
Бинарное
отношение на множестве
 называется предпорядком
на
называется предпорядком
на
 ,
если оно рефлексивно и транзитивно.
,
если оно рефлексивно и транзитивно.
Рефлексивное,
транзитивное и антисимметричное
отношение на множестве А называется
частичным
порядком на
 .
.
Такие бинарные отношения часто обозначаются символом «». Тогда аксиомы частичного порядка можно записать в виде:
1)
 для всех
для всех
 – рефлексивность;
– рефлексивность;
2)
из
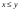 и
и
 следует x
= y
– антисимметричность;
следует x
= y
– антисимметричность;
3)
из
 и
и
 следует
следует
 – транзитивность.
– транзитивность.
