11. Закон распределения Релея.

Закон Релея применяется для описания неотрицательных величин, в частности, когда случайная величина является радиусом - вектором при двухмерном гауссовом распределении. Распределение является геометрической суммой случайных величин

X = (Y² + V²)^½ подчиненных закону Гаусса с параметрами a_y = a_V = 0, y = _V = ₀.

Плотность вероятности:

г де ₀ - среднее квадратическое отклонение исходного двухмерного распределения (₀ = _y = _V). Значение ₀ является параметром закона Рэлея. Функция распределения имеет вид:

При замене X новой переменной Z = x/₀ получим плотность вероятности и функцию распределения нормированного закона Рэлея:

Г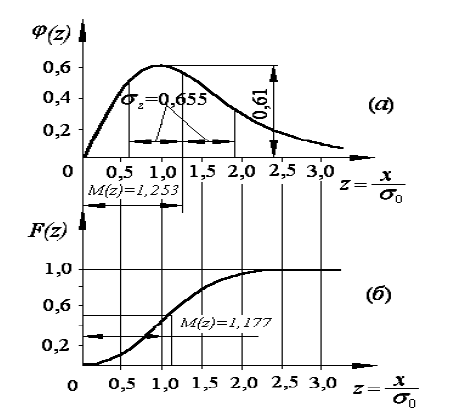 рафики нормированной плотности вероятности и функции распределения показаны на рис. Дифференциальная кривая (рис, а) имеет положительную асимметрию и более острую вершину, чем гауссово распределение.

МО, дисперсия: Асимметрия и эксцесс:

Нормированное рэлеевское распределение не зависит от параметра ₀

12. Биномиальный закон распределение и способы его получения.

Биномиа́льное распределе́ние — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна P (схема Бернулли).

Определение

Пусть X₁, … , X_n — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину Y: .

Тогда Y, число единиц (успехов) в последовательности X₁, … , X_n, имеет биномиальное распределение с n степенями свободы и вероятностью «успеха» p. Пишем: Y – Bin(n, p). Её функция плотности вероятности задаётся формулой:

где  — биномиальный коэффициент.

Функция распределения

, где обозначает наибольшее целое, не превосходящее число y.

Моменты

M_Y(t) = (pe^t + q)ⁿ, откуда мат ожидание - E[Y] = np, а дисперсия случайной величины – D[Y] = npq.

Свойства биномиального распределения

Пусть Y₁ – Bin(n, p) и Y₂ – Bin(n, 1 - p). Тогда р_Y1(k) = p_Y2(n - k).

Пусть Y₁ – Bin(n₁, p) и Y₂ – Bin(n₂, p). Тогда Y₁ + Y₂ – Bin(n₁ + n₂, p).

12. Закон распределения Релея-Райса.

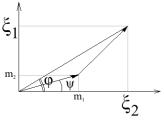
ω(ξ₁, ξ₂) = exp[- ]

ω(a, φ) = exp[- ] =

= exp[- ]

m₁ = m cosψ

m₂ = m sinψ

m(cosψ cosφ + sinψ sinφ) = m cos(φ - ψ)

ω(a, φ) = exp[- ]

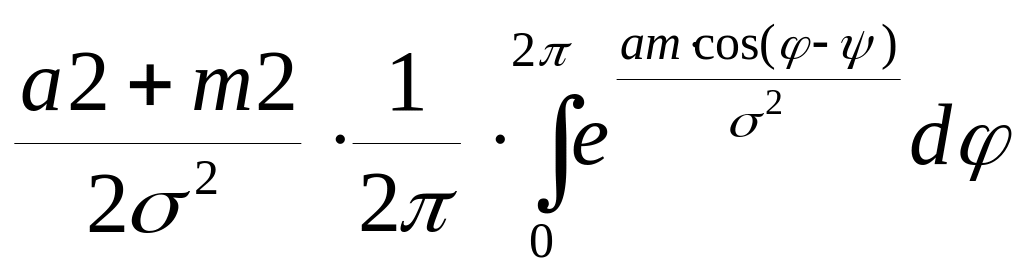ω(a) = exp[- ] = exp[- I_o( )] – закон распределения Релея-Райса

I_o(x) = - интеграл Бесселя

13. Пуассоновский закон распределения как предельный случай биномиального.

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Теорема Пуассона. Пусть и так, что . Тогда для любого вероятность получить k успехов в n испытаниях схемы Бернулли с вероятностью успеха p_n стремится к величине :

Доказательство. Положим . Тогда  и

В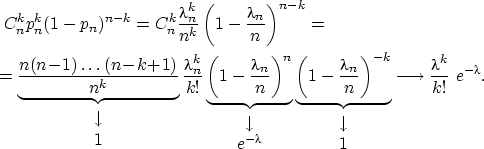 этом соотношении мы воспользовались тем, что и замечательным пределом . Докажем последнее свойство:

Говорят, что случайная величина ξ имеет распределение Пуассона с параметром , где , и пишут: , если ξ принимает значения с вероятностями  .

Схемой Бернулли называется последовательность независимых в совокупности испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом успех в одном испытании происходит с вероятностью , а неудача — с вероятностью q = 1 - p.