8. Теоремы сложения и умножения вероятностей.

Теорема сложения вероятностей.

Р(С)=Р(А)+Р(В)-Р(АВ), где Р(АВ) - вероятность одновременного наступления и события А, и события В.

Для несовместных событий:

P(A + B) = P(A) + P(B) - вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (и вообще для любого числа событий).

Теорема умножения вероятностей. Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Также можно записать:

Доказательство этой теоремы непосредственно вытекает из определения условной вероятности. Если события независимые, то , и теорема умножения вероятностей принимает вид:

В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события. Если в результате испытания может появиться n событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий

8. Характеристические и кумулянтные функции нормального, биномиального и пуассоновского законов распределения.

Н ормальный

По определению, характеристическая функция равна:

Её вычисление сводится к интегралу:

Кумулянтная: ψ(u) = ln φ(u) = -1/2u² σ²

Б иномиальный

Биномиальный закон представляет собой распределение вероятности следующего вида:

Тогда характеристическая функция для одного испытания имеет вид:

А для n испытаний: φ(u) = (q + pe^ju)ⁿ.

Кумулянтная: ψ(u) = ln((q + pe^ju)ⁿ) = n·ln(q + pe^ju).

П уассона

Характеристическая функция по определению:

_

Кумулянтная: ψ(u) = ln φ(u) = x(e^ju – 1)

9. Определение непрерывной случайной величины и её вероятностное описание.

Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Пример такой СВ: отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины: F(x) = P(ξ < x). Т.о. и здесь F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что СВ примет значение, меньшее чем х. Функция распределения является неубывающей и Значения функции распределения удовлетворяют неравенствам 0 ≤ F(x) ≤ 1. Вероятность попадания случайной величины в интервал x₁ ≤ ξ < x₂ равна приращению функции распределения на этом интервале. Случайная величина ξ называется непрерывной, если для нее существует

неотрицательная кусочно-непрерывная функция φ(x), удовлетворяющая для любых значений x равенству

Функция φ(t) называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁ < x₂, то: (23)

Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств x₁ ≤ ξ < x₂ равна площади криволинейной трапеции с основанием [x₁, x₂], ограниченной сверху кривой y = φ(x) (рис. 6).

Т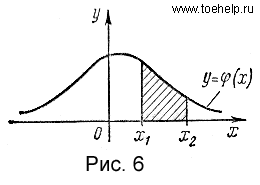 ак как , а , то (24)

Найдем F′(x) как производную интеграла по переменной верхней границе, считая плотность распределения φ(x) непрерывной: (25)

Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция φ(x) непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.

Полагая x₁ = x, x₂ = x + Δx имеем P(x ≤ ξ < x + Δx) = F(x + Δx) – F(x) = ΔF(x).

В силу непрерывности функции F(х) получим, что , следовательно  

Т. о, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю. Это не значит, что попасть в конкретное значение невозможно. В результате всегда получается конкретное значение, но в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение. Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.