6. Формула полной вероятности.
Пусть событие A
может произойти только вместе с одним
из попарно несовместных событий H1,
H2,
..., Hn,
образующих полную группу. Тогда, если
произошло событие A,
то это значит, что произошло одно из
попарно несовместных событий H1A,
H2A,
..., HnA.
Следовательно,
Применяя аксиому сложения
вероятностей, имеем
Но
(i=1,
2, ..., n), поэтому
или
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».
6. Линейная функция регрессии.
В
задаче нахождения функции регрессии
аппроксимируем ее прямой (иначе может
быть очень сложно найти ω(x2|x1),
но ошибка при этом увеличится): g(x1)
= c1x1
+ c2.
Таким образом, нужно найти коэффициенты
c1
и c2.
σ
2
= ∫∫(x2
– c1x1
–
c2)2
ω(x1,x2)dx1dx2
= (ξ2
– c1ξ1
–
c2)2
= ((ξ2
– a2)
– c1(ξ1
– a1)
– (c2
– a2
+ c1a1)2)
= (ξ2
– c1ξ1
– γ2)
, притом
что:
ξ1 = ξ1 – a1, ξ2 = ξ2 – a2, γ = (c2 – a2 + c1a1).
ξ22 + с12ξ12 + γ2 – 2c1ξ1ξ2 = σ22 + c12σ22 + γ2 – 2c1ρ = σ2 = f(с1,с2).
Нужно найти экстремум f (взять производные по c1 и c2 , приравнять их к нулю,...).
ρ – корреляция, ρ = ξ1ξ2 = ∫∫(x1 – a1)(x2 – a2) ω(x1,x2)dx1dx2, где a1 и a2 – средние значения соответственно ξ1 и ξ2.
(с какой вероятностью появляется плотность ω(x1,x2), с такой же появляется и (x1 – a1)(x2 – a2).
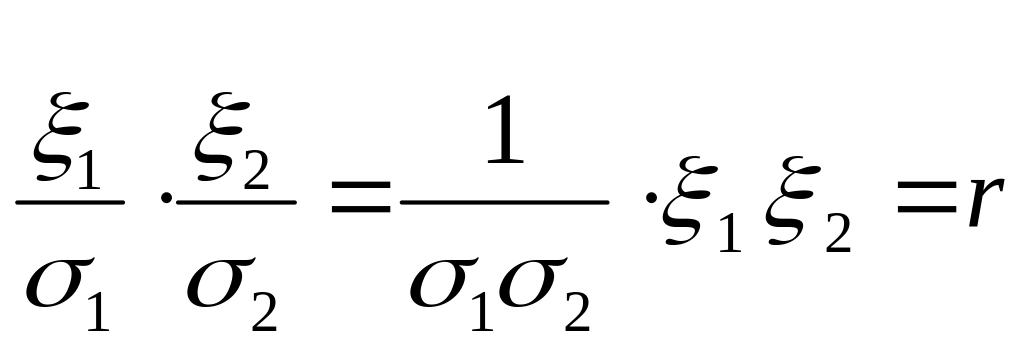
, r (|r|≤1) – коэффициент корреляции.
σ2 = σ22 + c12σ12 - 2σ1σ2 rc1+ γ2 , можно дополнить до полного квадрата:
σ2 = σ22 + c12σ12 - 2σ1σ2 rc1+ r2σ22 - r2σ22 + γ2 = σ22(1 – r2) + (c1σ1 - r2σ2)2 + γ2 - это должно быть минимально.
σ22(1 – r2) – сюда c1 и c2 не входят, значит это константа.
(c1σ1 - r2σ2)2 – всегда > 0. } значит минимум будет, когда
γ2 = (c2 – a2 + c1a1)2 – всегда > 0. } обе эти скобки равны нулю.
min σ2 = σ22(1 – r2)
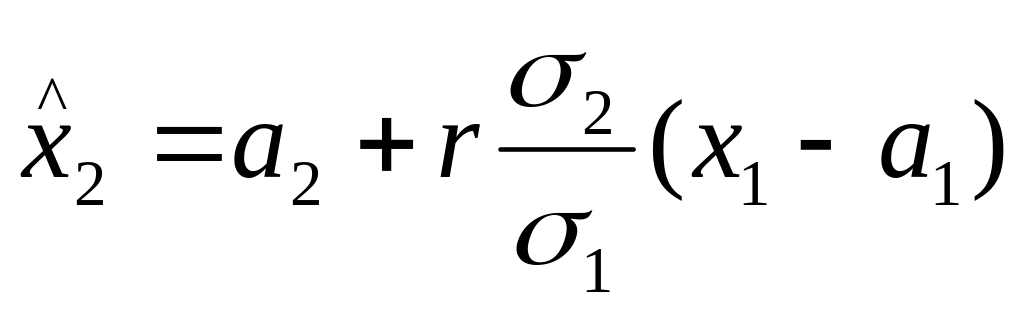удобно представлять
как:
,
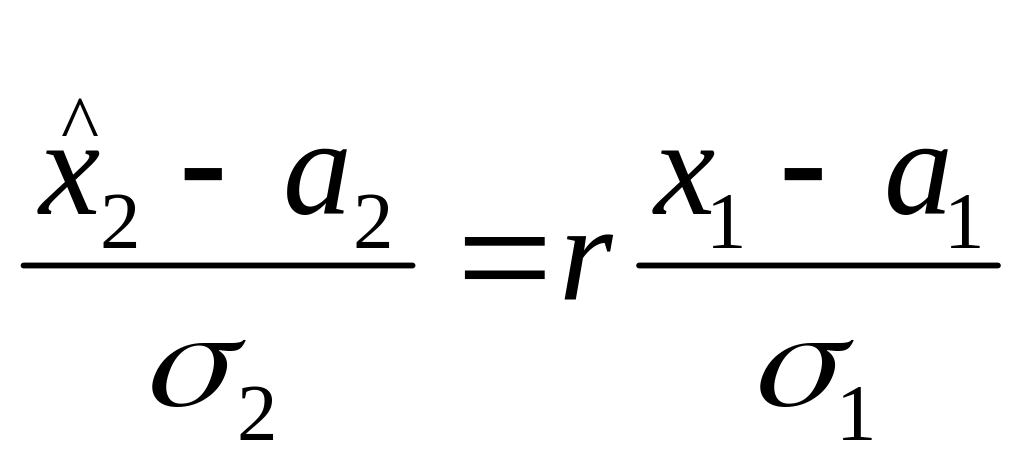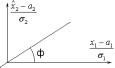
т.к.: 1)Прямая проходит через точку (0,0).
2)Коэффициент корреляции r = tg(ф).
Если r = 0, то линейная зависимость отсутствует, полная независимость не следует.
7. Формула Байеса.
Также называется теорема гипотез. Является следствием теремы умножения и формулы полной вероятности.
Решаемая задача: есть полная группа несовместых гипотез H1, H2, ..., Hn с известными вероятностями соответственно р(H1), р(H2), ..., р(Hn). Произведен опыт, в результате которого наблюдено появление некоторого события А. Спрашивается: как следует изменить вероятности гипотез в связи с появлением этого события?
По сути надо найти условную вероятность р(Нi|А) для каждой гипотезы.
Из теоремы умножения: р(АНi) = р(А)р(Нi|A) = p(Hi)p(A|Hi).
О
тсюда
р(Нi|A)
= p(Hi)p(A|Hi)
/ р(А).
Представив р(А) по формуле полной вероятности ( ), получим:
- формула Байеса.
Везде i = 1, 2, …, n.
7. Применение линейной функции регрессии в задаче измерения физической величины.
Рассм. задачу измерения физической величины. Берем линейку, меряем длину стола. Получаем результат измерения (но не оценку!).
Тут есть один трудный момент: истинная длина стола на самом деле случайна!
Берем две случайные величины ξ1 и ξ2 , в результате измерений получим значение: x1 – результат измерения. x2 – истинная длина стола. ^x2 = c1x1 + c2. Нужно найти c1, c2, погрешность.
На глаз, интуитивно можно прикинуть, что стол не длиннее 2м и не короче 1м:
ω(x2), a2 – средняя длина стола, σ22 – дисперсия (это априорные сведения). «Стол реализовался».
Введем физическую модель зависимости ξ1 и ξ2: ξ1 = ξ2 + Δ.
П
огрешность
прибора не зависит от измерения, тогда
среднее суммы равно сумме средних,
дисперсия суммы равна сумме дисперсий:
, σ12 = σ22 + σΔ2. _
a1 = a2, для простоты считаем, что Δ = 0.
,
r = ρ/(σ1 σ2) = σ22/(σ1 σ2) = σ2/σ1
^x2 – a2 = (σ22/σ12)(x1 - a1) = (1/(1 + σΔ2/σ22)) (x1 – a2)
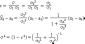
Далее возможны варианты по упрощению:
1) σ2 >> σΔ , тогда ^x2 = x1
2) σ2 << σΔ , тогда ^x2 = a2