17. Определение энергетического спектра случайного процесса.

Энергетический спектр случайного процесса – это средний спектр по ансамблю (среднее по ансамблю).

Для случайного процесса характерно то, что его значение в некоторый момент времени t является случайной величиной. Например, если взять несколько одинаковых электронных усилителей, находящихся в одинаковых условиях, и будем наблюдать изменения шумовых напряжений на выходах, то для любого момента времени t эти напряжения на выходах разных усилителей будут в общем случае различны и непредсказуемы. К выходному напряжению каждого из усилителей мы можем применить преобразование Фурье и определить спектр шумового сигнала. Можно так же найти усредненный спектр – энергетический спектр случайного процесса.

Наиболее простой в смысле мат описания, но типичный для многих реальных процессов – это случайный процесс, обладающий свойствами стационарности и эргодичности. Стационарность означает, что характеристики случайного процесса при равных условиях не зависят от того, когда мы наблюдаем этот процесс. Эргодичность говорит о том, что рассматриваемый процесс может быть усреднен по времени, вместо усреднения по множеству.

Д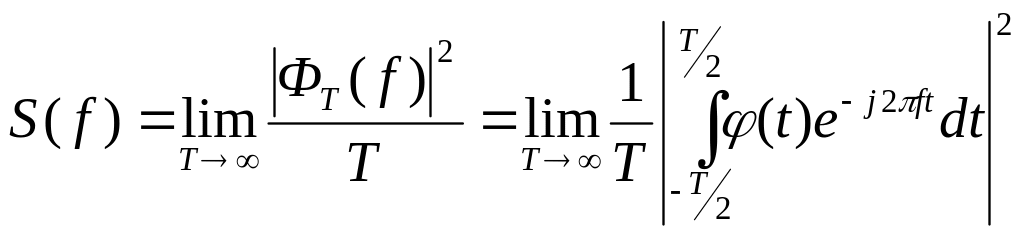 ля стационарного эргодического случайного процесса спектр мощности определяется исходя из условия, что время наблюдения → ∞

Ф_Т(f) – спектр энергии (спектральная плотность энергии).

Энергетический спектр случайного процесса является неслучайной функцией частоты

18. Методы увеличения длины периода псевдослучайной последовательности.

Пусть генератор сгенерировал две последовательности с периодами n₁ и n₂ (- взаимно простые числа, т.е. не имеющие общих множителей). Тогда последовательность, получающаяся следующим образом, может иметь период p=n₁n₂

1ая послед-ть с периодом n₁=3: 532 532 532 532 532 532 …

2ая послед-ть с периодом n₂=4: 1628 1628 1628 1628 …

Сложение по модулю m (m=10) [т.е. например: 5+8=13, остаток от 13/10=3, пишем 3]:

532 532 532 532 532 532 …

162 816 281 628 162 8 …

694 348 713 150 694

p= n₁n₂n₃ если последовательности три.

Это скорее всего мультипликативный метод, т.к. периоды умножаются.

Есть еще метод смешанного типа.

x_i+1 = (ax_i + ) (mod m)

a и  подбираются экспериментально.

При всем этом есть 3 свойства: 1) последовательность должна быть хорошая (хорошая – это с максимальным периодом), 2) соседнее значение должно быть независимо 3) с какой-то степенью должно удовлетворять критерию согласия.

18. Точечные оценки параметров и их свойства.

Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям, критериям. Путь θ_n – статистическая оценка неизвестного параметра θ теоретического распределения.

Допустим, что по выборке объема n найдена θ_n.

Существуют 4 характеристики качественной оценки:

1) Состоятельная оценка. Такой оценкой называют оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру:

θ_n → θ при n → ∞, P(|θ_n – θ|< ε) → 1 при n → ∞.

2) Несмещенная оценка. Такой оценкой называют оценку θ*, мат ожидание которой равно оцениваемому параметру θ при любом объеме выборки. M(θ*) = θ

Смещенной называют оценку, мат ожидание которой не равно оцениваемому параметру. θ_n – θ = b_n(θ), где b_n(θ) – смещение.

b_n(θ) = aθ + b. θ_n – θ = aθ + b Берем дробь в качестве новой оценки. Она уже несмещенная.

3) Эффективной называется оценка, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

4 ) Достаточная оценка. Такая оценка, если θ_n содержит всю информацию о параметре θ, который содержится в x.

Пусть имеется случайная величина x с мат ожиданием m и дисперсией D. Оба параметра неизвестны. Над величиной x произведено n независимых опытов, давших результаты x₁, x₂, … x_n. Требуется найти состоятельные и несмещенные оценки для m и D.

В качестве оценки для мат ожидания:

Оценка является состоятельной. Эффективность или неэффективность оценки зависит от вида закона распределения величины x. Если x распределена по нормальному закону, то оценка эффективная.

Оценка дисперсии:

Эта оценка состоятельная. Однако это смещенная оценка, так как её мат ожидание не равно D, а несколько меньше. Формула для состоятельной и несмещенной оценки: