1. Предмет и аксиомы теории вероятностей

ТВ – математич наука, изучающая закономерности в случайных явлениях.

Случайное явление – которое при неоднократном воспроизведении протекает каждый раз несколько по-иному. (Пример: стрельба из орудия – снаряд каждый раз попадает в разные места из-за различных побочных факторов (браке изготовления снаряда и подобных). Т.о. общим предметом полета снаряда занимаются другие науки (физика, например), а вот при оценке побочных факторов подключается теория вероятностей со своими собственными подходами (решая вопросы вроде: что нужно сделать, чтобы поразить цель с вероятностью 0,7 и прочие подобные). При этом ТВ не занимается досканальным расмотрением одного снаряда, принимая во внимание всё новые побочные факторы - это трудоёмко и бессмысленно, ТВ пытается найти закономерности во всем комплексе случайных явлений (например: при стрельбе в мишень в одну точку, сначала закономерность не будет видна (попадать будем в разные места), потом в точке прицела попадания будут сгущаться (получится нормальное распределение)).

В основе любой теории лежит опыт, на котором строятся аксиомы и модель того объекта, который изучается.

Аксиома – концентрированный опыт, выраженный в предложении.

Событие – факт, который может произойти при определенном комплексе условий.

Комплекс условий – контролируемая совокупность параметров.

n(A)/n – относительная частота появления события A, где n(A) – кол-во появлений события А, n – кол-во испытаний в опыте.

АКСИОМА: вероятность – это число 0<=p<=1, которое ставится в соответствие некоторому событию и обладает устойчивостью относительно частоты появления. Также важна массовость (на примере стрельбы в мишень по двум выстрелам ничего не ясно, а при увеличении кол-ва выстрелов явно видна закономерность).

ТВ не противопоставляет себя другим наукам, а наоборот дополняет их, позволяя исследовать своими методами то, что нельзя исследовать методами других точных наук.

1. Нормальный закон распределения и центральная предельная теорема.

Говорят, что ξ имеет нормальное (гауссовское) распределение с параметрами a и σ², где , , и пишут: , если ξ имеет следующую плотность распределения:

Убедимся, что является плотностью распределения. Т. к. для всех , то свойство (f1) выполнено. Проверим (f2):

где через I обозначен табличный интеграл (интеграл Пуассона)

Нормальное распределение N_0,1 с параметрами a = 0 и σ² = 1 называется стандартным нормальным распределением. Плотность стандартного нормального распределения равна .

Центральная предельная теорема (Ляпунова)

Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному. На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

2. Классическое определение вероятности. Геометрические вероятности.

При большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. P(A) ≈ P*(A). Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности). Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно). События E₁,E₂, ..., E_N в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A. Классическое определение вероятности: Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий: P(A) = M/N.

Геометрическая вероятность применяется там, где классический метод не подходит из-за бесконечного числа исходов. Пример:

З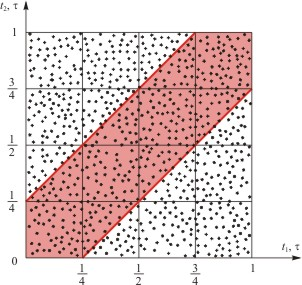 адача про встречу:

Двое приятелей договорились встретиться в выбранном месте от 12 до 13 часов. Каждый приходит в некоторый случайный момент времени, ждет другого 15 минут и уходит. Условие успешности попытки встречи таково: второй приятель приходит не позже, чем через 15 мин после первого, и не раньше, чем за 15 мин до первого: t_1n – 1/4 ч ≤ t_2n ≤ t_1n + 1/4 ч.

Т очки, удовлетворяющие этому условию, лежат между двумя прямыми, уравнения которых t₂ = t₁ – 1/4 и t₂ = t₁ + 1/4. При увеличении числа испытаний точки ложатся внутри квадрата «все более равномерно», а отношение удачных испытаний ко всем вообще испытаниям стремится к отношению площади полосы между указанными прямыми к площади всего квадрата. Площадь квадрата, естественно, равна 1, а площадь полосы 7/16. Следовательно, вероятность того, что приятели встретятся, равна 7/16.

Задача Бюффона:

П лоскость разлинована параллельными прямыми, находящимися друг от друга на расстоянии 1. Игла длины 1 падает на плоскость случайным образом. Какова вероятность, что игла пересечет какую-либо начерченную прямую? Пусть игла каким-то образом упадет и прямая, ближайшая к ее центру, находится от этого центра на расстоянии d. Ясно, что d ≤ 1/2. Угол α между иглой и прямой лежит на отрезке от 0 до π/2. Условие, согласно которому игла пересекает прямую, d > (1/2) sin α. Фактически, задача свелась к следующей. На плоскости с координатами (α, d) в прямоугольнике (0 ≤ α ≤ π/2; 0 ≤ d ≤ 1/2) наугад выбирается точка; какова вероятность, что она окажется ниже синусоиды d = (1/2) sin α? P = S₁ / S₂, где S₁ – площадь между осью абсцисс и синусоидой, S₂ – площадь всего прямоугольника (0 ≤ α ≤ π/2; 0 ≤ d ≤ 1/2). S₂ = π/4. S₁ = 1/2.