
- •7. Закон больших чисел
- •7.1. Принцип практической уверенности. Формулировка закона больших чисел
- •7.2. Неравенства Маркова и Чебышева
- •Выражения (7.1–7.2) справедливы для дискретных и непрерывных случайных величин.
- •7.3. Теорема Чебышева (частный случай)
- •7.4. Теорема Бернулли
- •7.5. Теорема Пуассона
7.4. Теорема Бернулли
Пусть произведено п независимых испытаний, в каждом из которых вероятность появления некоторого события А постоянна и равна Р.
Теорема Бернулли. При неограниченном возрастании числа независимых испытаний п относительная частота m/n появления события А сходится по вероятности к вероятности p события А, т. е.
![]()
где
ε
–
сколь угодно малое положительное число.
Для конечного n
при
условии, что
![]() ,
неравенство Чебышева для случайной
величины m/n
будет иметь вид
,
неравенство Чебышева для случайной
величины m/n
будет иметь вид
P(|m/n–p|< ε) ≥1– pq/(n ε2). (7.8)
Каким бы малым ни было число ε, при n → ∞ величина дроби pq/(n∙ε2)→0, а P(|m/n–p|< ε)→1.
Из теоремы Бернулли следует, что при достаточно большом числе испытаний относительная частота т/п появления события практически утрачивает свой случайный характер, приближаясь к постоянной величине p – вероятности данного события. В этом и состоит принцип практической уверенности.
Пример 7.6. С целью установления доли брака по схеме возвратной выборки было проверено 1000 единиц продукции. Какова вероятность того, что установленная этой выборкой доля брака по абсолютной величине будет отличаться от доли брака по всей партии не более чем на 0,01, если что в среднем на каждые 10 000 изделий приходится 500 бракованных?
Решение. По условию задачи число независимых испытаний n = 1000.
p = 500/10 000 = 0,05; q = 1 – p = 0,95; ε = 0,01. P(|m/n–p| < 0,01?
Применив формулу (7.8), получим
P(|m/n–p| < 0,01) ≥ 1–pq/(nε2) = 1–0,05∙0,95/(1000∙0,0001) = 0,527.
Итак, с вероятностью не менее 0,527 можно ожидать, что выборочная доля брака (относительная частота появления брака) будет отличаться от доли брака во всей продукции (от вероятности брака) не более чем на 0,01.
Пример 7.7. При штамповке деталей вероятность брака составляет 0,05. Сколько нужно проверить деталей, чтобы с вероятностью не менее 0,95 можно было ожидать, что относительная частота бракованных изделий будет отличаться от вероятности брака менее чем на 0,01?
Решение. По условию задачи р = 0,05; q = 0,95; ε = 0,01.
P(|m/n–p|< 0,01) ≥ 0,95; n = ? Из равенства 1–pq/(nε2) = 0,95
находим:
n = pq/(0,05ε2) = 0,05∙0,95/(0,05∙0,0001) = 9500.
Замечание. Оценки необходимого числа наблюдений, получаемые при применении теоремы Бернулли (или Чебышева) очень преувеличены. Существуют более точные оценки, предложенные Бернштейном и Хинчиным, но требующие применения более сложного математического аппарата. Чтобы избежать преувеличения оценок, иногда пользуются формулой Лапласа
P(|m/n–p|<ε)
≈ 2Φ0
![]() .
.
Недостатком этой формулы является отсутствие оценки допускаемой погрешности.
7.5. Теорема Пуассона
В теореме Бернулли устанавливается связь между относительной частотой появлений события и его вероятностью p при условии, что последняя от опыта к опыту не изменяется. Теорема Пуассона устанавливает связь между относительной частотой появления события и некоторой постоянной величиной при переменных условиях опыта.
Теорема Пуассона. Если производится n независимых опытов и вероятность появления события А в i-м опыте равна pi, то при увеличении n относительная частота появления события m/n сходится по вероятности к среднему арифметическому значению вероятностей pi, т. е.
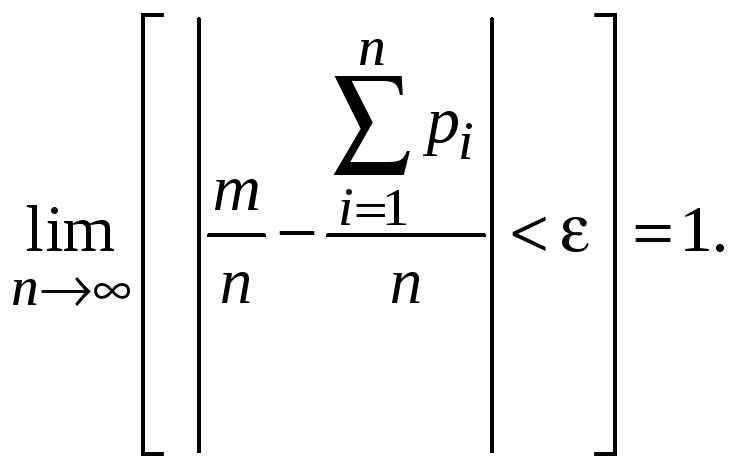 (7.9)
(7.9)
Для конечного n будем иметь:
 (7.10)
(7.10)
Каким
бы ни было ε,
при
n→
∞ величина дроби
 ,
а вероятность
,
а вероятность
![]()
Пример 8.9. Одинаковые партии изделий размешены в 11 ящиках, причем доли первосортных изделий в них составляют 0,0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0.8; 0,9; 1,0. Из каждого ящика наудачу извлечено по одному изделию. Определим вероятность того, что доля первосортных изделий в выборке будет отличаться от средней арифметической доли менее чем на 0,2.
Решение. По условию задачи: n = 11; p1 = 0,0; p2 = 0,1; p3 = 0,2; p4 = = 0,3; p5 = 0,4; р6 = 0,5; p7 = 0,6; p8 = 0,7; p9 = 0,8; p10 = 0,9; p11 = 1,0; ε = 0,2.
Применив формулу (7.10), получим
 =
=
= 1–0,0 + 0,09 + 0,16 + 0,21 + 0,24 + 0,25 + 0,24 + 0,21 + 0,16 + 0,09 +
+ 0,0)/(121∙0,04) = 1–1,165/4,84 = 0,64.
