5.4. Построение разверток

Разверткой называется фигура, полученная при совмещении поверхности с плоскостью. Естественно, что замкнутая поверхность не может быть совмещена с плоскостью без разрывов. Предварительно поверхность разрезают по некоторым линиям, а затем совмещают ее с плоскостью. Построение разверток поверхностей представляет большой практический интерес при конструировании различных сооружений и изделий из листового материала. На развертке сохраняются длины линий, лежащих на поверхности, величины углов между линиями и площади фигур, образованных замкнутыми линиями. Для построения развертки поверхности необходимо знать закон преобразования направляющих линий поверхности в линии на плоскости развертки и закон распределения прямых линий, соответствующих образующим поверхности. Закон преобразования поверхности в развертку может быть задан как аналитическими зависимостями, так и графическим алгоритмом.

Уже в самых первых сочинениях по начертательной геометрии хорошо отработаны алгоритмы построения точных разверток цилиндра, конуса и торса геликоида (открытой винтовой поверхности). Под разверткой поверхности понимается совмещение части (отсека) поверхности с плоскостью. Часть цилиндра разрезается одной из образующих и совмещается с плоскостью. Развертка боковой поверхности прямого кругового цилиндра изображается в виде прямоугольника высотой l и длиной πd, где l – длина образующей цилиндрической поверхности, d – диаметр основания цилиндра (рис. 5.19).

Рис. 5.19. Развертка прямого кругового цилиндра

Кроме прямых линий изгиба и кручения на развертке можно провести множество других прямых линий, которым на поверхности соответствуют геодезические линии, определяющие кратчайшие расстояния между точками поверхности. На цилиндрической и конической поверхности геодезической линией является винтовая линия.

Разверткой прямого кругового конуса является сектор круга с радиусом l и углом φ, равным или 2π∙cosβ, где l – длина образующей, d – диаметр основания конуса (рис. 5.20). Конус и цилиндр рассматриваются как частный случай поверхности с ребром возврата, когда ребро возврата вырождается в конечную и бесконечно-удаленную точку. Коническая поверхность также имеет две полы, лежащие с разных сторон от вершины конуса.

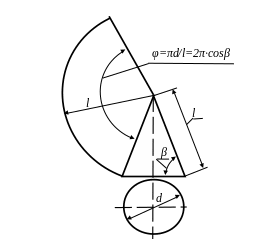
Рис. 5.20. Развертка прямого кругового конуса

На рис. 5. 21 приведен пример построения развертки одной полы геликоида, ограниченного ребром возврата (гелисой – цилиндрической винтовой линией с диаметром d), горизонтальными плоскостями с расстоянием между ними равным h (высотой h). Поверхность разрезается по ребру возврата и одной из образующих и совмещается с плоскостью. Винтовая линия на развертке преобразуется в дугу окружности с радиусом ρ и углом φ. Длина дуги окружности равна длине винтовой линии (L=π d/ cosβ). Величину радиуса ρ определим из равенства 2 π ρ φ/360°= π d/ cosβ. Откуда ρ = d 180°/ cosβ∙φ. Образующие геликоида параллельны образующим направляющего конуса, отсюда сумма углов между образующими геликоида равна сумме углов между направляющими конуса (φ = 2π∙cosβ). Если вместо φ подставить его значение, то получим ρ = d / 2cosβ².

Поверхностью с ребром возврата имеет две полы, лежащие с разных сторон от точек касания. Если ребром возврата является плоская кривая линия, то поверхность превращается в плоскость.

На линейчатых поверхностях общего вида можно выделить линии сжатия (горло однополостного гиперболоида, линия сужения косой плоскости, стрикционные линии цилиндроида и т.п.), на которых пересекаются близлежащие образующие поверхности. Линии сжатия являются аналогом ребра возврата, с той лишь разницей, что образующие не касаются линии сжатия, а пересекают её под каким-либо углом. Поверхности цилиндрические, конические и с ребром возврата можно получить из плоскости развертки с помощью деформации изгиба. Линейчатые поверхности общего вида получаются из плоскости развертки с помощью деформации кручения и изгиба. Отметим также, что из плоскости развертки можно с помощью изгиба получить поверхность только теоретически, а практически наличие деформаций сжатия и растяжения неизбежно, так как не существует изделий без толщины.

φ=2πcosβ

ρ

L

h

β

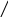
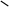
d

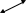
πd

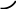
Рис. 5. 21. Развертка эвольвентного (открытого) геликоида

Развертка поверхности отсека прямого закрытого геликоида с шагом Н и диаметром цилиндрической винтовой линии d представляет собой неполное кольцо (рис. 5.22). Шаг винтовой поверхности разворачивается в длину дуги окружности диаметром d₁, Тогда, Н = π d₁ ∙ φ/360° . Определим величину угла φ из полученной зависимости: φ = Н ∙360°/π d₁. Винтовая линия разворачивается в длину дуги окружности диаметром D. Тогда, L = πd/cosβ = π D ∙ φ/360°. D = d + d₁. Подставим значение D в предыдущее выражение: L = πd/cosβ = π(d + d₁) ∙ φ/360°. Определим величину угла φ, φ = πd360°/cosβ(d + d₁). Величина диаметра d₁ может определена из сравнения формул для определения угла φ: d₁ = Нd cosβ/(π²d – Нcosβ) или d₁ = d sinβ/(π –sinβ).

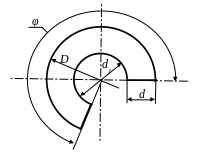
Рис. 5.22. Развертка прямого закрытого геликоида

Развертка поверхности отсека кольцевого закрытого геликоида с шагом Н и диаметрами внутренней и наружной цилиндрических винтовых линий d и d׳ также представляет собой неполное кольцо (см. рис. 5.22). Внутренняя винтовая линия разворачивается в длину дуги окружности диаметром d׳.Тогда, L׳ = πd/cosβ = π d׳ ∙ φ/360°. Определим величину угла φ, φ = d360°/cosβ d׳. Наружная винтовая линия разворачивается в длину дуги окружности диаметром D. Тогда, L = πd/cosβ = π D ∙ φ/360°. D = (d – d׳) + d₁. Подставим значение D в предыдущее выражение: L = πd/cosβ = π(d – d׳+ d₁) ∙ φ/360°. Определим величину угла φ, φ = d360°/cosβ(d – d׳+ d₁).

Разверткой поверхности отсека косого закрытого геликоида является закрученное кольцо, образующие поверхности на развертке касаются окружности некоторого радиуса. Разверткой поверхности отсека однополостного гиперболоида вращения является также закрученное кольцо, образующие поверхности на развертке касаются окружности некоторого радиуса. Горло поверхности разворачивается в дугу окружности внутренней дуги окружности, а основание однополостного гиперболоида разворачивается в дугу окружности внешней дуги окружности. Для построения развертки линейчатой поверхности необходимо знать закон преобразования направляющих линий поверхности в линии на плоскости развертки и закон распределения прямых линий, соответствующих образующим поверхности. Закон преобразования поверхности в развертку может быть задан как аналитическими зависимостями, так и графическим алгоритмом. Развертка линейчатой поверхности строится для одной полы ограниченной части поверхности. Разделение поверхности на полы происходит по линии сжатия.

Если неизвестна закономерность перехода от поверхности к развертке, то строится приближенная развертка. Для этого поверхность заменяется вписанной или описанной многогранной поверхностью и строится ее развертка. Если поверхность разбивается на множество треугольников, то способ называется триангуляцией. Построение развертки связано с определением натуральной величины каждой грани. Рассмотренные на предыдущих лекциях метрические задачи являются составной частью построения развертки. Построение разверток – это комплексная метрическая задача, в которой важно рационально организовать графические построения, чтобы добиться точности и быстроты построения.

Для усеченного цилиндра и конуса, также для наклонных цилиндрических и конических поверхностей и других поверхностей строят приближенные развертки, так как недостаточно исследованы вопросы построения разверток: необходимо установить геометрическую проекционную связь между поверхностями и их развертками.

Рассмотрим пример построения развертки призмы методом раскатки и методом нормального сечения. Разрежем призму по ребру АА^׳ и будем вращать ее грани вокруг ребер до совмещения с фронтальной плоскостью, проходящей через ребро АА^׳. Точки В, В^׳, С и С^׳ при вращении перемещаются в плоскостях, перпендикулярных к ребрам (рис.5.23). От точки А₂ проведем дугу радиусом А₁В₁ до пересечения с перпендикуляром из В₂ к А₂А₂^׳ и получим В_о. Аналогично получаем остальные точки. Пристроим нижнее и верхнее основания и получим полную развертку призмы. Рассечем призму плоскостью α, перпендикулярной к ребрам, и определим натуральную величину сечения А"В"С"^׳, например совместив его с π₁. Нормальное сечение разворачивается в прямую линию А_оВ_оС_о.

С₂^׳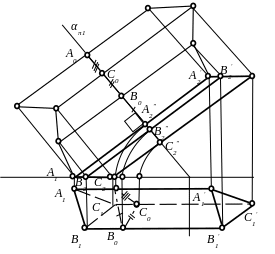

Рис. 5.23. Развертка наклонной призмы

На практике для неразрывающихся нелинейчатых поверхностей также строят развертки, для этого их аппроксимируют развертывающимися поверхностями (разбивают их на части, которые заменяют плоскостями или развертываемыми поверхностями, т.е. вписывают или описывают вокруг них несколько цилиндрических, конических или других поверхностей), а затем строят для них развертки. Полученная развертка всей поверхности является условной, так как состоит из множества отдельных плоских фигур, для получения поверхности их необходимо склеивать между собой и отдельные участки подвергать сжатию и растяжению. Чем больше число разбиений, тем меньше кусочки, на которые распадается поверхность. Это принципиальное отличие условной развертки от приближенной.