5.3. Решение метрических задач на измерение углов. Схема решения задач на измерение углов

Из двух смежных углов, которые получаются при пересечении двух прямых линий а и b, будем условно рассматривать меньший по величине α. Угол между скрещивающимися прямыми линиями а и b определяется как угол между пересекающимися прямыми линиями а и b^*. Для этого через любую точку на прямой линии а проводится b^*параллельно заданной прямой линии b. B общем случае угол α между двумя прямыми линиями может проецироваться в виде различных углов от 0° до 180° (0° ≤ α ≤180°), и, наоборот, угол α´ может быть проекцией любого угла в пределах от 0° до 180° (0° ≤ α´ ≤ 180°).

Если обе стороны угла параллельны плоскости проекций, то на эту плоскость проекций угол проецируется без искажения в натуральную величину.

Выделим следующие задачи на измерение углов:

1У – определение угла между двумя прямыми линиями,

2У – определение угла между прямой линией и плоскостью,

3У – определение угла между двумя плоскостями

Решения указанных задач связаны и могут быть сведены к ключевым задачам на определение натуральной величины отрезка прямой линии и проведения перпендикуляра к плоскости. Схема решения метрических задач на измерение углов приведена на рис. 5.13.

Проведение

перпендикуляра

н.в. отрезка

1У

2У

3У

Рис. 5.13. Схема решения метрических задач на измерение углов

В общем случае для того, чтобы определить величину угла между прямыми линиями, необходимо плоскость угла преобразовать в плоскость уровня. Наиболее рациональным методом для решения этой задачи является вращение вокруг линии уровня. Проведем в плоскости угла линию уровня, например горизонталь (рис. 5.14). Затем повернем плоскость угла вокруг горизонтали до положения, параллельного горизонтальной плоскости проекций, тогда все отрезки и углы буду изображаться в натуральную величину. Точки 1 и 2 пересечения сторон угла с горизонталью неподвижны.

Рис. 5. 14. Определение величины угла между прямыми линиями

методом вращения вокруг линии уровня

Вершина угла А перемещается по окружности с радиусом ОА в горизонтально проецирующей плоскости β, перпендикулярной к горизонтали. Для построения повернутого положения вершины А определим натуральную величину радиуса вращения и отложим её на следе плоскости β_π1. Можно также через вершину угла провести фронталь до пересечения с горизонталью в точке 3, далее проводим дугу из центра 3₁ радиусом равным фронтальной проекции фронтали А₂3₂ до пересечения со следом плоскости β_π1. Угол 1₁А^*2₁ является натуральной величиной угла α.

Угол φ между прямой линией и плоскостью определяется как угол между прямой линией и её проекцией на эту плоскость (рис. 5.15).

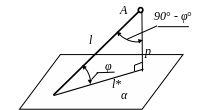
Рис. 5.15. Угол между прямой линией и плоскостью

Угол между прямой линией АВ и плоскостью проекций (π₁ или π₂) определяется как угол между натуральной величиной прямой и её проекцией на эту плоскость проекций (рис. 5.16).

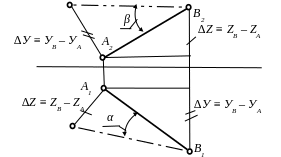
Рис. 5.16. Углы между прямой линией и плоскостями проекций

Если необходимо определить угол между прямой линией l и плоскостью общего положения, то можно искомый угол определять как дополнительный угол до 90° угла между прямой линией и перпендикуляром к этой плоскости. Для этого из любой точки А прямой линии опускается перпендикуляр р к плоскости α, а далее определяется величина угла между прямыми линиями l и р (см. рис. 5. 14). Двугранный угол между двумя плоскостями и измеряется линейным углом, образованный перпендикулярами в заданных плоскостях и к ребру двугранного угла. Если заданы проецирующие плоскости, а значит и ребро двугранного угла занимает проецирующее положение, то угол можно измерить непосредственно на чертеже без дополнительных построений (рис. 5.17).

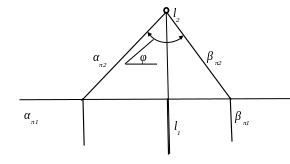
Рис. 5.17. Угол между проецирующими плоскостями

Для определения угла между двумя плоскостями общего положения можно преобразовать чертеж так, чтобы ребро стало проецирующим. При определении угла между заданной плоскостью и плоскостью проекций проводят линию наибольшего наклона. Линией наибольшего наклона называется линия плоскости, проходящая перпендикулярно к линии уровня. Линией наибольшего наклона к горизонтальной плоскости проекций называется линией ската, проходящей перпендикулярно к горизонтали. Угол между линией наибольшего наклона и плоскостью проекций является углом наклона заданной плоскости и плоскости проекций. Эта задача может рационально решаться методом прямоугольного треугольника и методом перемены плоскостей проекций.

Вместо угла между двумя плоскостями можно определять угол между перпендикулярами к этим плоскостям и дополнять его до 180° (рис. 5.18).

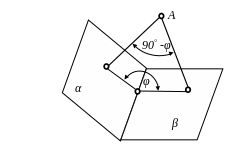
Рис. 5.18. Угол между двумя плоскостями как угол дополнительный до 180° угла между перпендикулярами к плоскостям