4.3.5. Пересечение многогранников. Сетка Ананова

Решение позиционных задач на пересечение многогранников сводится к рациональному сочетанию позиционных задач на пересечение прямой линии с плоскостью или пересечение плоскостей. Сложность решения таких задач заключается в громоздкости построений. В пересечении поверхностей двух многогранников получаются одна или несколько плоских или пространственных ломаных линий. Для того чтобы не упустить построение точек линии пересечения и правильно соединить полученные точки, а также определить видимость на чертеже можно использовать схему, называемую сеткой Ананова (профессор Санкт-Петербургского политехнического института Давид Георгиевич Ананов предложил этот метод). Сетка Ананова представляет собой наложение условных разверток (без соблюдения метрических характеристик) многогранников друг на друга. Правила сетки Ананова заключаются в следующем: 1) линии пересечения не должны пересекать сетку, 2) линия пересечения должна быть замкнутая, 3) на невидимых гранях лежат невидимые линии пересечения. Рассмотрим пример пересечения двух призм (рис. 4.14).

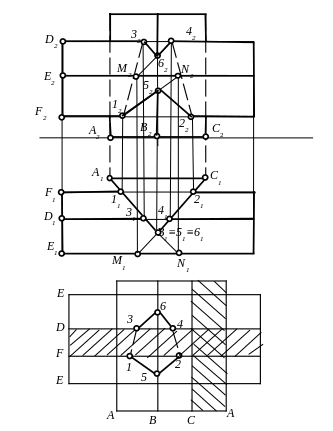
Рис. 4.14. Пересечение двух призм. Сетка Ананова

Построим точки пересечения двух призм и нанесём их на условные развертки поверхностей, наложенные друг на друга. Нанесем штриховку на невидимые грани призм. Предположим, что мы упустили построение одной точки, например точки 6. Тогда у нас, на сетке Ананова, не получается замкнутая линия. Выявив ошибку, найдем точку 6, и соединим полученные точки на ортогональном чертеже в том же порядке, как на сетке Ананова. Сетка Ананова может использоваться и при решении задач на пересечение двух линейчатых поверхностей. Тогда заданные поверхности рассматриваются как многогранники.

4.4. Пересечение поверхностей.

Для определения линия пересечения двух поверхностей можно использовать различные способы решения: метод концентрических сферических посредников, метод эксцентрических сферических посредников, метод секущих плоскостей, преобразования чертежа и определение линии пересечения из условия принадлежности поверхности. Выбор метода решения зависит от характера задаваемых поверхностей, их взаимного положения и расположения по отношению к плоскостям проекций.

4.4.1. Метод концентрических сферических посредников.

Метод концентрических сферических посредников является уникальным способом, так как позволяет решать задачи в одной проекции. Сущность этого способа заключается в том, что две поверхности вращения с общей осью пересекаются по окружностям, которые на плоскости проекций, параллельной оси вращения, изображаются отрезками прямых линий, проходящих через точки пересечения очерков поверхностей. Так, например, пересечение цилиндрической поверхности и одной полы конической поверхности происходит по окружности q (рис. 4.15). Пересечение сферы с поверхностью вращения происходит также по окружностям, если центр сферы лежит на оси поверхности вращения (рис. 4.16). Таким образом, если заданы две поверхности вращения с пересекающимися осями, то сфера с центром в точке пересечения осей пересекает заданные поверхности по окружностям. Если оси поверхностей параллельны плоскости проекций, то плоскости получаемых окружностей перпендикулярны к этой плоскости проекций и изображаются в виде отрезков прямых линий. Окружности, получаемые в пересечении сферы с одной и другой поверхностью, пересекаются между собой в двух точках. В проекции, параллельной общей плоскости симметрии поверхностей, точки пересечения попарно сливаются в одну.

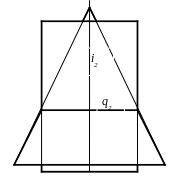
Рис. 4.15. Пересечение поверхностей вращения с общей осью

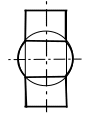
Рис. 4.16. Пересечение сферы с поверхностью вращения

Рассмотрим пример построения линии пересечения двух поверхностей вращения (конуса и цилиндра) методом сфер. Поверхности заданы очерками во фронтальной проекции (рис 4.17). При этом подразумевается, что оси поверхностей вращения пересекаются в одной точке и заданные поверхности имеют общую фронтальную плоскость симметрии. Точку пересечения осей вращения поверхностей выбирают за центр вспомогательных сфер.

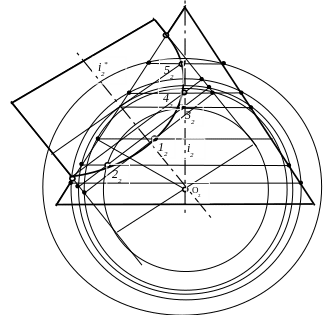
Рис. 4.17. Метод концентрических сферических посредников

Для построения точек линии пересечения проводится несколько сфер различного радиуса. Вспомогательная сфера, касательная к цилиндру, не пересекается с конусом, а значит, не может быть использована для построений. Вспомогательная сфера, касательная к конусу, пересекается с цилиндром по двум окружностям и является сферой минимального радиуса пригодной для построений. Из точки пересечения осей опустим перпендикуляр на образующую конуса и этим радиусом проведем фронтальный очерк сферы. Через точку основания перпендикуляра проходит окружность касания сферы с конусом, которая изображается отрезком прямой линии, перпендикулярной к оси конуса. Через точки пересечения очерка сферы и цилиндра проходят окружности пересечения сферы с цилиндром, которые изображаются отрезками прямых линий, перпендикулярных к оси цилиндра. На пересечении проведенных отрезков (в пространстве окружностей) получаются общие точки поверхностей. Увеличивая радиус сферы, и повторяя этот прием несколько раз, можно получить множество точек линии пересечения. Очерки заданных поверхностей лежат в одной фронтальной плоскости, поэтому точки их пересечения также принадлежат линии пересечения. Вспомогательные сферы, имеющие радиус больше расстояния от центра сфер до этих точек, определяют мнимые точки пересечения. При пересечении поверхностей вращения меньшая поверхность врезается в большую поверхность. Для определения, какая именно поверхность больше, а какая меньше, сравнивают сферы касательные к заданным поверхностям.

Метод сфер используют для построения линии пересечения поверхностей вращения с пересекающими осями и общей плоскостью симметрии параллельной плоскости проекций, на которой выполняются построения.