Метрологическая оценка ошибки кмд типа float. (оценка ошибки «отображение – воспроизведение»)
Метрологическая оценка F-множеств float,
адекватная максимально возможной ошибке
преобразования входной модели данных,
находится в пределах
,
где S – порядок старшего бита. Характер
ее изменения от S иллюстрируют рис.5.
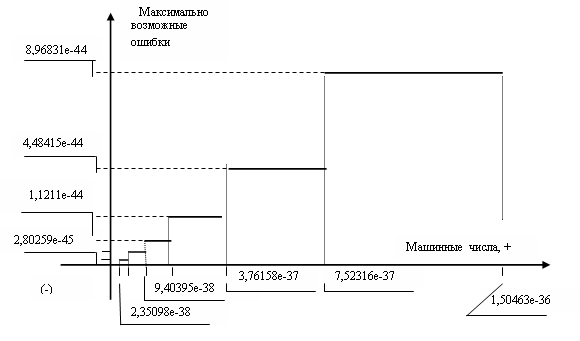
Рис. 5.1. Максимально возможные ошибки преобразования входной модели данных фактор-множеств компьютерных чисел типа float.
С исчерпывающей полнотой характеристики оценки ошибки «отображение – воспроизведение» определяются функцией плотности распределения для КМД
Исчерпывающие характеристики оценки плотности распределения для КМД типа float, предоставляются системой гистограмм, отображающих средние свойства вариационного ряда рассматриваемого множества. Для исследования плотности КМД типа float была построена система гистограмм с последовательно увеличивающимся числом участков разбиения.
Результаты построения приведены на рис.6
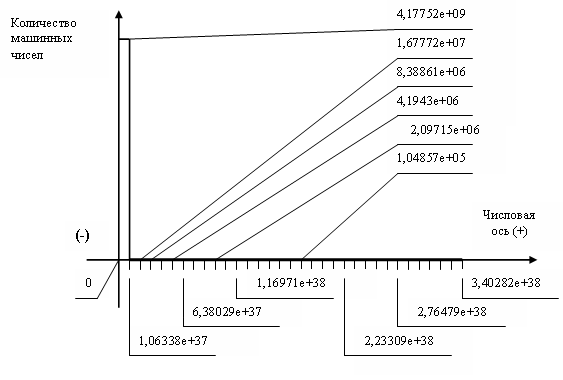
а)
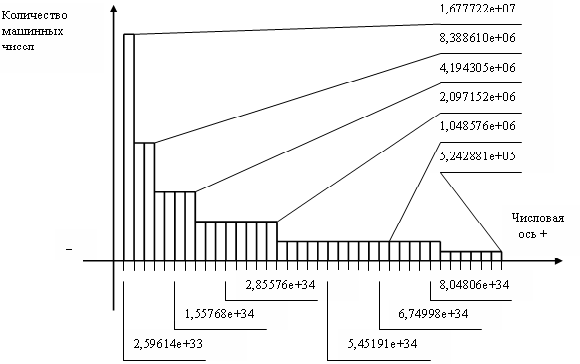
б)
Рис.6.1. Тридцать два участка ()
Первые Тридцать два участка
а) полная гистограмма б) Гистограмма построена начиная со второго участка вариационного ряда
Нетрудно заметить, что качественные характеристики комп-пространства исходов вероятностной модели чисел обладают устойчивостью и к вариации типомоделей Float-Point процессоров
Т.е., не умаляя общности, исследование топологии комп-чисел, равно, как и метрологические свойства «отображения-воспроизведения» (в т.ч., и погрешностей арифметических операций) может быть проведено на упрощенной модели.
Например, на Пр = (4,4,2)
Наиболее наглядно характер распределения машинных флоат-чисел виден на модельном флоат-процессоре (p,m) = (4,4)
Размах вариационного ряда машинных чисел (p,m) = (4,4) – float – формата (табл. 1) определяется [min, max] = [0,00390625, 240] [минимальное (машинный ноль),
Совокупность значений чисел заданного формата (p,m) = (4,4) приведена в табл. 1, используемой далее для формирования вариационных рядов и полигонов частостей (гистограмм) машинных чисел.
Общее
количество чисел в табл. 1 равно
.
Таблица 1.
Множество значений чисел (p,m) = (4,4) – float‑формата.
|
мантисса |
1111 |
1110 |
1101 |
1100 |
1011 |
1010 |
1001 |
1000 |
порядок |
|
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
111 |
7 |
240 |
224 |
208 |
192 |
176 |
160 |
144 |
128 |
110 |
6 |
120 |
112 |
104 |
96 |
88 |
80 |
72 |
64 |
101 |
5 |
60 |
56 |
52 |
48 |
44 |
40 |
36 |
32 |
100 |
4 |
30 |
28 |
26 |
24 |
22 |
20 |
18 |
16 |
11 |
3 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
10 |
2 |
7,5 |
7 |
6,5 |
6 |
5,5 |
5 |
4,5 |
4 |
1 |
1 |
3,75 |
3,5 |
3,25 |
3 |
2,75 |
2,5 |
2,25 |
2 |
0 |
0 |
1,875 |
1,75 |
1,625 |
1,5 |
1,375 |
1,25 |
1,125 |
1 |
1111 |
-1 |
0,9375 |
0,875 |
0,8125 |
0,75 |
0,6875 |
0,625 |
0,5625 |
0,5 |
1110 |
-2 |
0,46875 |
0,4375 |
0,40625 |
0,375 |
0,34375 |
0,3125 |
0,28125 |
0,25 |
1101 |
-3 |
0,234375 |
0,21875 |
0,203125 |
0,1875 |
0,171875 |
0,15625 |
0,140625 |
0,125 |
1100 |
-4 |
0,1171875 |
0,109375 |
0,1015625 |
0,09375 |
0,0859375 |
0,078125 |
0,0703125 |
0,0625 |
1011 |
-5 |
0,05859375 |
0,0546875 |
0,05078125 |
0,046875 |
0,04296875 |
0,0390625 |
0,03515625 |
0,03125 |
1010 |
-6 |
0,029296875 |
0,02734375 |
0,025390625 |
0,0234375 |
0,021484375 |
0,01953125 |
0,017578125 |
0,015625 |
1001 |
-7 |
0,0146484375 |
0,013671875 |
0,0126953125 |
0,01171875 |
0,0107421875 |
0,009765625 |
0,0087890625 |
0,0078125 |
Так как качественные характеристики комп-пространства исходов обладают устойчивостью относительно вариации типомоделей Float-Point процессоров, то не умаляя общности исследование топологии множества комп-чисел может быть проведено на упрощенной модели, например, Пр = (4,4,2). В этом случае
определяя как
количество строк таблицы, и соответственно
количество столбцов таблицы как-
.
Совокупность значений чисел формата (p,m) = (4,4) заданного пространства исходов приведена в табл. 2. Общее количество чисел в табл. 2 согласно (11), (12) равно
.
Отметим, что устойчивость (и регулярность) топологического строения множеств комп-чисел типомоделей процессоров отражается в возможности описания фактор-классов этого множества отдельными строками таблицы чисел.
Еще более наглядно регулярность структуры отражается при их графической интерпретации соответствующими характеристическими конусами, отображающими регулярный характер и строения, топологии фактор-множеств, и регулярный характер их построения, рис. 1.
y =x/8
y =x/16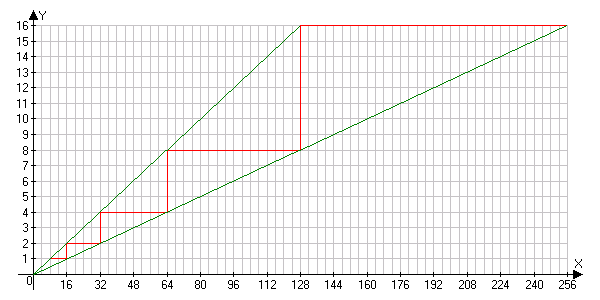
Рис.1. Графическая интерпретация пространства исходов Dc типомодели (4,4,2).
Действительно, каждая из ступеней графика отвечает строке таблицы и соответсвующему фактор-классу множества машинных чисел рассматриваемой типомодели процессора
Линии, соединяющие минимальные (максимальные) числа смежных фактор-классов - суть образующие прямые фактор-классов рассматриваемой типомодели процессора.
Уравнения образующих
прямых процессора (4,4,2), см. рис. 1, которые
одновременно ограничивают график сверху
и снизу, суть
и
.
Аналогично строятся, описываются, и факторизуются множества комп-чисел для других рассматриваемых типомоделей процессоров.