Обчислення вагових коефіцієнтів високочастотного, смугового і режекторного фільтрів

Вагові коефіцієнти високочастотного (ФВЧ), смугового (СФ) та режекторного (РФ) фільтрів можна обчислити на основі підсумування спектральних перетворень [1, 26].

В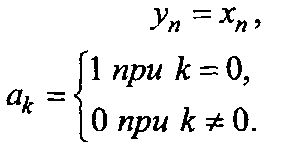 ведемо поняття всечастотного (ВФ) фільтра, який пропускає, не послаб­люючи, усі частоти. Рівняння такого фільтра має вигляд

а його ваговий коефіцієнт

Отже, ВФ фільтр має лише один коефіцієнт а₀=1. На основі цього можна стверджувати: якщо від спектра ВФ фільтра відняти спектр ФНЧ, то отримаємо спектр ФВЧ із тією самою граничною частотою (рис. 1.4). Це означає, що вагові коефіцієнти ФВЧ можуть бути обчислені як

(1.11)

Рис. 6.4. Формування передаточної функції ФВЧ фільтра з

передаточних функцій ВФ та ФНЧ фільтрів

Вагові коефіцієнти смугового фільтра визначають так. За основу беремо ФНЧ₂ з граничною частотою щ, яка відповідатиме верхній частоті смугового фільтра. Від спектра ФНЧ₂ віднімаємо спектр іншого ФНЧ_Х, гранична частота ω₁ якого є меншою. В результаті отримаємо спектр смугового фільтра із зоною попускання між ω₁ і ω₂ (Рис. 1.5).

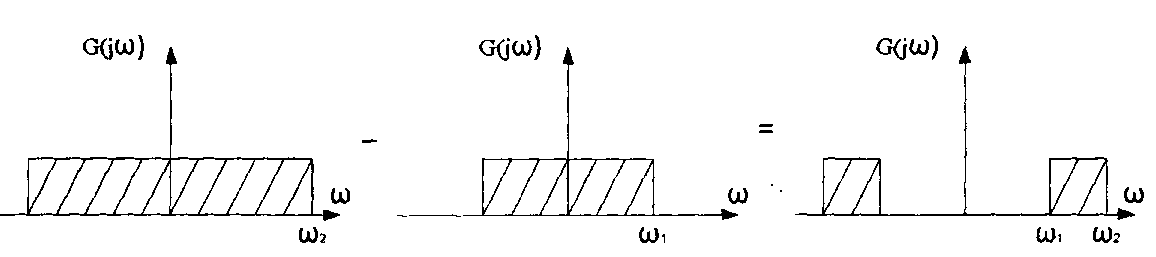
Рис. 6.5. Формування передаточної функції СФ фільтра з

передаточних функцій ФНЧ₂ та ФНЧ± фільтрів

Вагові коефіцієнти смугового СФ фільтра знаходять так

(1.12)

Обчислюють вагові коефіцієнти режекторного РФ фільтра, віднімаючи від спектра ВФ фільтра спектр СФ фільтра (рис. 1.6).

Рис. 6.6. Формування передаточної функції РФ фільтра

з передаточних функцій ВФ та СФ фільтрів

Вагові коефіцієнти режекторного РФ фільтра визначають за формулою (1.13)

2. Рекурсивні цифрові фільтри

У загальному випадку вихідний сигнал ЦФ у момент часу t = nT визна­чають значенням вхідного сигналу х у цей самий момент часу, а також значеннями вхідних і вихідних сигналів у попередні моменти часу, тобто [26]

Якщо ця залежність є лінійною, то цифровий фільтр називається ліній­ним, а вихідна величина у_п визначається:

(1.14)

або в загальному випадку

(1.15)

Більше з двох чисел М і L вказує на порядок фільтра.

Очевидно, єдиним обмеженням фізичної реалізації різницевого рівняння є неможливість одержання якого-небудь з доданків правої частини, оскільки відповідний доданок ще не з’явився і не може бути отриманий його запам’ятовуванням з метою затримки на задану кількість періодів квантування. Отже, ЦФ може бути фізично реалізованим, якщо в праву частину рівняння входять поточні і минулі значення вхідної величини, але не входять майбутні значення.

Лінійний дискретний фільтр звичайно описують за допомогою переда­точної функції, під якою розуміють відношення Z -перетворення вихідної величини до Z -перетворення вхідної величини. Таке перетворення ставить у відповідність дискретному залежному від часу сигналу х(пT_а) функцію X(z) комплексної змінної z. У цьому випадку подання передаточної функції розглядатися не буде, однак використається одна з важливих властивостей Z - перетворення, яка пов’язана з тим, що при Z -перетворенні множення на Z^-1 спричиняє затримку сигналу на величину періоду дискретизації Т_а. Ця властивість буде використана під час побудови блок-схеми ЦФ. Вхідні вели­чини, починаючи з x_n+N, затримуються кожна на величину періоду диск­ретизації Т_а до початкового значення x_n-_N. Кожна величина перемножується на відповідний коефіцієнт фільтра а_k. Добутки підсумовують для утворення вихідної величини у_п.

Отже, з рівняння (1.14) видно, що для одержання у_п необхідно виконати такі операції:

1. Отримати сигнали х_п-х,...,х_п-т,у_п-х,...у_п-l. їх можна одержати з х_п і у_n за допомогою реалізації затримок на один період дискретизації Т_а. У разі апаратної, мікропроцесорної реалізації цифрового фільтра для отримання затриманих сигналів використовують стек.

2. Перемноження одержаних на елементах затримки сигналів на постійні коефіцієнти а_т і b_l.

3. Підсумування отриманих сигналів, яке може бути реалізовано програмно або на суматорах.

Згідно з (1.4) побудована блок-схема симетричного нерекурсивного ЦФ (рис. 1.7).

Рис. 1.7. Блок-схема нерекурсивного фільтра

У рекурсивних фільтрах існує зворотний зв’язок за вихідним сигналом, який може спричиняти нестабільність. У випадку збудження такого фільтра вхідним сигналом його вплив теоретично ніколи не зникає. На рис. 1.8 наведена блок-схема рекурсивного фільтра, яка побудована згідно з (1.15). Схема такого фільтра вимагає М + L аперіодичних ланок і М + L +1 перемножувачів.

Імпульсний відгук рекурсивного цифрового фільтра розглянемо на прик­ладі. Нехай ЦФ рекурсивного типу описують таким диференціальним рів­нянням

Н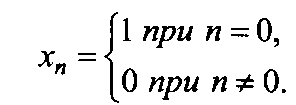 а його вхід подається одиничний імпульс

Рис. 1.8. Блок-схема рекурсивного фільтра

Початково фільтр не був збуджений і його вихідний сигнал дорівнював нулю (у_п-1 = 0). Якщо подати на вхід одиничний імпульс, на виході фільтра сформуються такі вихідні сигнали (рис. 1.9):