
- •1.Первообразная и неопределенный интеграл. Свойства неопределенного интеграла
- •2.Таблица интегралов
- •3.Замена переменной в неопределенном интеграле
- •4 Метод интегрирования по частям для неопр.Интеграла
- •5. Простейшие дроби и их интегрирование
- •6. Разложение рациональных дробей на простейшие и их интегрирование
- •8. Интегрирование рациональных дробей общего вида
- •11.Определенный интеграл
- •12. Теорема о среднем. Производная интеграла по переменному верхнему пределу
- •13. Формула Ньютона – Лейбница
- •14. Замена переменной в определенном интеграле
- •15. Интегрирование по частям в определенном интеграле
- •16. Несобственные интегралы 1-го и 2-го рода
- •17,18.. Геометрические приложения определенных интегралов
- •19. Определение двойного интеграла,св-ва.
- •20. Изменение порядка интегрирования в двойном интеграле
- •22. Свойства сходящихся числовых рядов.
- •29. Признак Даламбера.
- •30. Интегральный признак Коши.
- •32. Абсолютную сходимость.
- •36. Свойства степенных рядов
- •39.Ряд Маклорена
- •40. Остаточный член формулы Тейлора
- •41.Некотореы разложения в ряды Тейлоре и маклорена
1.Первообразная и неопределенный интеграл. Свойства неопределенного интеграла
Определение: Если функция F(x) – первообразная для f(x) на промежутке (a;b), то множество функций F(x)+C – неопределённый интеграл от f(x).
∫f(x)dx=F(x)+C, где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, dx – переменная интегррования.Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции F'(x) = f(x).
Обозначение
![]() где
F'(x) = f(x). Функция f(x) называется
подынтегральной функцией, а выражение
f(x)dx - подынтегральным выражением.
Свойства неопределенного интеграла.1.
Производная неопределенного интеграла
равна подынтегральной функции;
дифференциал от неопределенного
интеграла равен подынтегральному
выражению, т.е.
где
F'(x) = f(x). Функция f(x) называется
подынтегральной функцией, а выражение
f(x)dx - подынтегральным выражением.
Свойства неопределенного интеграла.1.
Производная неопределенного интеграла
равна подынтегральной функции;
дифференциал от неопределенного
интеграла равен подынтегральному
выражению, т.е.
![]()
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
![]()
3. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
![]()
4 . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.
2.Таблица интегралов
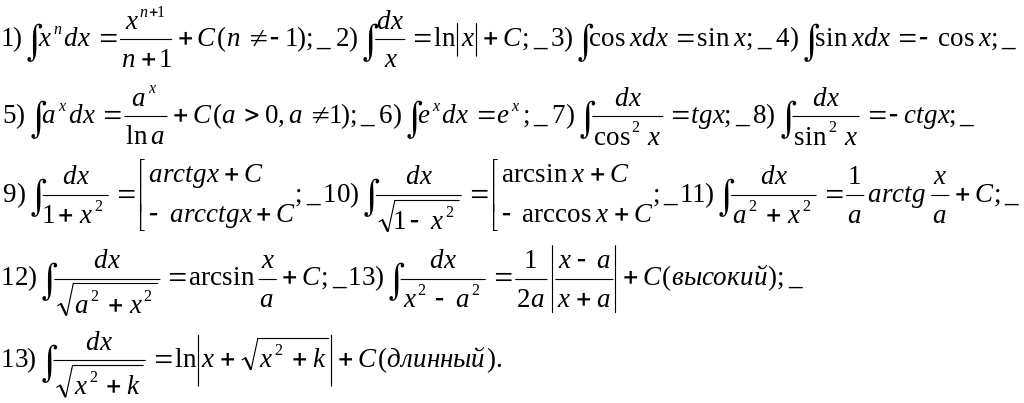
3.Замена переменной в неопределенном интеграле
Методом подстановки (заменой переменной) называется метод, при котором введение новой переменной позволяет свести исходный интеграл к табличному.
Теорема:
Пусть функция x=(t)
определена и дифференцируема на некотором
множестве Т, и пусть Х-множество значений
этой функции. На множестве Х определена
функция y=f(x),
тогда если на Х функция f(x)
имеет первообразную, то на Т справедлива
формула:![]()
4 Метод интегрирования по частям для неопр.Интеграла
Метод
интегрирования по частям
позволяет свести исходный неопределенный
интеграл к более простому виду либо к
табличному интегралу. Этот метод наиболее
часто применяется, если подынтегральная
функция содержит логарифмические,
показательные, обратные тригонометрические,
тригонометрические функции, а также их
комбинации. Формула
интегрирования по частям
следующая
![]() .
.
То
есть, подынтегральное выражение f(x)dx
представляем в виде произведения функции
u(x)
на d(v(x))
- дифференциал функции v(x).
Далее находим функцию v(x)
(чаще всего методом
непосредственного интегрирования)
и d(u(x))
- дифференциал функции u(x).
Подставляем найденные выражения в
формулу интегрирования по частям и
исходный неопределенный интеграл
сводится к разности
![]() .
Последний неопределенный интеграл
может быть взят с использованием любого
метода
интегрирования,
в том числе и метода интегрирования по
частям.
.
Последний неопределенный интеграл
может быть взят с использованием любого
метода
интегрирования,
в том числе и метода интегрирования по
частям.
5. Простейшие дроби и их интегрирование
1 тип.
![]() —
заданные
числа
—
заданные
числа![]()
![]()
2 тип.
![]() —
заданные
числа
—
заданные
числа![]()
![]()
3 тип
![]() —
заданные
числа
—
заданные
числа![]()
Квадратный
трехчлен![]() не
имеет действительных корней.
не
имеет действительных корней.
Интегрирование
проводится путем выделения полного
квадрата в знаменателе:![]() и
последующей заменой
и
последующей заменой![]() т.е.
т.е.
![]()
![]()
![]()
Первый
интеграл при помощи замены![]() приводится
к табличному (ОК № 15, формула 2), второй
является табличным (формула 15). Пример:
приводится
к табличному (ОК № 15, формула 2), второй
является табличным (формула 15). Пример:
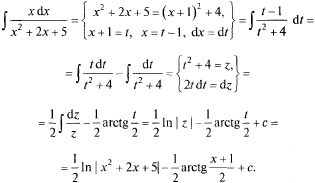
4
тип.![]() —
заданные числа
—
заданные числа![]() не имеет действительных корней.
не имеет действительных корней.
