1) Определение. Две прямые называются скрещивающими­ся, если они не лежат в одной плоскости.

Докажем теорему, которая выражает признак скрещи­вающихся прямых.

Теорема

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту п лоскость в точ­ке, не лежащей на первой прямой, то эти прямые скрещиваю­щиеся.

Доказательство. Рассмотрим прямую АВ, лежащую в плоскости ά, и прямую СD, пересекающую эту плоскость в точке С, не лежащей на прямой АВ. Докажем, что АВ и СD — скрещивающиеся прямые, т. е. они не лежат в одной плоскости. Действительно, если допустить, что прямые АВ и СD лежат в некоторой плоскости β, то плоскость β будет проходить через прямую АВ и точку С и поэтому совпадет с плоскостью ά. Но это невозможно, так как прямая СD не лежит в плоскости ά.

Теорема доказана.

Итак, возможны три случая взаимного расположения двух прямых в пространстве:

а) прямые пересекаются, т. е. имеют только одну общую точку;

б) прямые параллельны, т. е. лежат в одной плоскости и не пересекаются;

в) прямые скрещивающиеся, т. е. не лежат в одной плоскости;

Докажем еще одну теорему о скрещивающихся прямых.

Теорема

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой п рямой, и притом только одна.

Доказательство

Рассмотрим скрещивающиеся прямые АВ и СD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой СD, и притом только одна.

Проведем через точку A прямую АЕ, параллельную прямой СD, и обозначим буквой ά плоскость, проходящую через прямые АВ и АЕ. Так как прямая СD не лежит в плоскости ά и парал­лельна прямой АЕ, лежащей в этой плоскости, то прямая СD параллельна плоскости ά.

Ясно, что ά — единственная плоскость, проходящая через прямую АВ и параллельная прямой СD. В самом деле, любая другая плоскость, проходящая через прямую АВ, пересекается с прямой АЕ, а значит, пересекается и с параллельной ей пря­мой СD.

Теорема доказана.

2) Теорема

Если прямая перпендикулярна к двум пере­секающимся прямым, лежащим в плоскости, то она перпенди­кулярна к этой плоскости.

Доказательство

Рассмотрим прямую а, которая перпендикулярна к прямым p и q, лежащим в плоскости ά и пере­секающимся в точке О. Докажем, что а ά. Для этого нужно доказать, что прямая а перпендикулярна к произ­вольной прямой m плоскости ά.

Рассмотрим сначала случай, когда прямая а проходит через точку О. Проведем через точку О прямую l, парал­лельную прямой m (если прямая m проходит через точку О, то в качестве l возьмем саму прямую m). Отметим на прямой а точки А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости а прямую, пересекающую прямые p, q и l соответственно в точках Р, Q и L. Будем считать для определен­ности, что точка Q лежит между точками Р и L.

Так как прямые p и q — серединные перпендикуляры к отрез­ку АВ, то АР = ВР и AQ = ВQ. Следовательно, АРQ= ВРQ по трем сторонам. Поэтому АРQ= ВРQ.

Сравним теперь треугольники АРL и ВРL. Они равны по двум сторонам и углу между ними (АР= ВР,PL—общая сторона, АРL— ВРL), поэтому АL — ВL. Но это означает, что тре­угольник АВL равнобедренный и его медиана LO является высо­той, т. е. l а. Так как l||т и l а, то т а (по лемме о перпен­дикулярности двух параллельных прямых к третьей). Таким обра­зом, прямая а перпендикулярна к любой прямой т плоскости ά, т. е. а ά.

Рассмотрим теперь случай, когда прямая а не проходит через точку О. Проведем через точку О прямую а₁, параллельную пря­мой а. По упомянутой лемме а₁ р и а₁ q, поэтому по доказан­ному в первом случае а₁ ά. Отсюда (по первой теореме п. 16) следует, что а ά.

Теорема доказана.

БИЛЕТ№5

1) Параллельность прямой и плоскости. Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаим­ного расположения прямой и плоскости в пространстве:

а) прямая лежит в плоскости;

б) прямая и плоскость имеют только одну общую точку, т. е. пересекаются;

в) прямая и плоскость не имеют ни одной общей точки.

Определение. Прямая и плоскость называются парал­лельными, если они не имеют общих точек.

Параллельность прямой а и плоскости а обозначается так: а|| ά. Наглядное представление о прямой, параллельной плос­кости, дают натянутые троллейбусные или трамвайные провода — они параллельны плоскости земли. Другой пример дает линия пересечения стены и потолка — эта линия параллельна плоскости пола. Заметим, что в плоскости пола имеется прямая, параллельная этой линии. Такой прямой является, например, линия пересечения пола с той же самой стеной. На рисунке указанные прямые обозначены буквами а и b. Оказывается, что если в плоскости ά имеется прямая b, параллельная прямой а, не лежащей в плоскости ά, то прямая а и плоскость ά парал­лельны. Другими словами, наличие в плоскости ά прямой b, параллельной прямой а, является признаком, по которому можно сделать вывод о параллельности прямой а и плоскос­ти ά. Сформулируем это утверждение в виде теоремы.

Т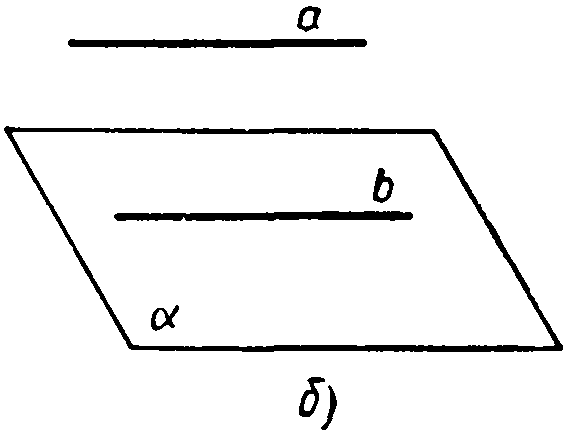 еорема

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Доказательство

Рассмотрим плоскость ά и две парал­лельные прямые а и b, расположенные так, что прямая b лежит в плоскости ά, а прямая а не лежит в этой плоскости. Докажем, что а||ά. Допустим, что это не так. Тогда прямая а пересекает плоскость ά, а значит, по лемме о пересечении плоскос­ти параллельными прямыми прямая b также пересекает плос­кость ά. Но это невозможно, так как прямая b лежит в плоскости ά. Итак, прямая а не пересекает плоскость ά, поэтому она парал­лельна этой плоскости.

Теорема доказана.

Д окажем еще два утверждения, которые часто используются при решении задач.

1 . Если плоскость проходит через данную прямую, парал­лельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Пусть через данную прямую а, параллельную плоскости ά, проходит плоскость β, пересекающая плоскость ά по прямой b. Докажем, что b||a. Действительно, эти прямые лежат в одной плоскости (в плоскости β) и не пересекаются: ведь в против­ном случае прямая а пересекала бы плоскость ά, что невозможно, поскольку по условию а||ά.

2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

В самом деле, пусть а и b — параллельные прямые, причем прямая а параллельна плоскости ά. Тогда прямая а не пере­секает плоскость ά, и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая b также не пере­секает плоскость ά. Поэтому прямая b либо параллельна плос­кости ά, либо лежит в этой плоскости.