Тема 10. Несинусоидальные токи

12.1. Несинусоидальные периодические токи и их представление в виде тригонометрического ряда

До сих пор мы рассматривали линейные цепи переменного тока с синусои­дальными э.д.с. Но на практике э.д.с. и токи довольно часто отличаются от сину­соидальных. Например, в генераторах переменного тока вследствие того, что ин­дукция распределяется в теле статора не по синусоидальному закону, э.д.с., кото­рые наводятся в обмотках, также несинусоидальны (рис.12.1).

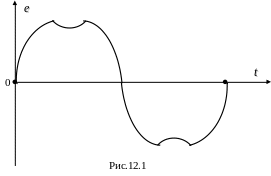
Явления, которые происходят в линейных цепях при периодических, но неси­нусоидальных э.д.с. или токах, проще всего исследовать, если э.д.с. или токи раз­ложить в тригонометрический ряд Эйлера-Фурье:

,

(12.1)

где при k = 0, А_km = А₀, а φ_k = ψ₀ = 90º.

Первый член ряда А₀ называется постоянной составляющей или нулевой гар­моникой, второй член – основной синусоидой или первой гармони­кой, а все последние члены вида при k > 1 носят назва­ние высших гармоник.

Тригонометрический ряд после преобразования синуса суммы каждой гар­моники можно еще записать так:

(12.2)

где .

Если несинусоидальная функция соответствует условию:

f(ωt) = –f(ωt + π),

то в этом случае ряд не содержит чётных гармоник и постоянной составляющей. Одна из таких функций изображена на рис.12.2. Она расположена симметрично относительно оси абсцисс.

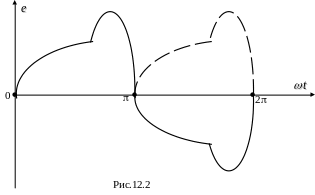
Если несинусоидальная функция соответствует условию:

f(ωt) = f(–ωt),

то ряд не содержит синусов. Одна из таких функций изображена на рис.12.3. Она расположена симметрично относительно оси ординат.

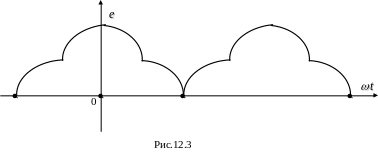
Возможные другие варианты несинусоидальных функций.

12.2 Коэффициенты формы, амплитуды и искажения

Введём понятие действующего и среднего значения несинусоидального тока.

Под действующим значением несинусоидального тока понимаем силу такого эквивалентного постоянного тока, который, проходя по цепи с тем же со­противлением, которое и переменный несинусоидальный ток, выделяет за период такое же количество тепла, что и переменный несинусоидальный ток:

.

(12.3)

Среднее значение несинусоидального тока

.

(12.4)

Можно доказать, что действующее значение несинусоидального тока зависит только от действующих значений отдельных гармоник и не зависит от их фазы:

.

(12.5)

Аналогично

.

(12.6)

В технике сильных токов для оценки несинусоидальности периодических на­пряжений и токов используют коэффициенты: формы k_ф, амплитуды k_а и искаже­ния k_и.

Коэффициент формы – это отношение действующего значения, например, тока, к его среднему значению:

.

(12.7)

Для синусоиды

.

Коэффициент амплитуды – это отношение максимального значения, напри­мер, тока, к его действующему значению:

.

(12.8)

Для синусоиды

.

Коэффициент искажения – это отношение действующего значения основной гармоники, например, тока, к действующему значению несинусоидаль­ного тока:

.

(12.9)

Для синусоиды k_и = 1.
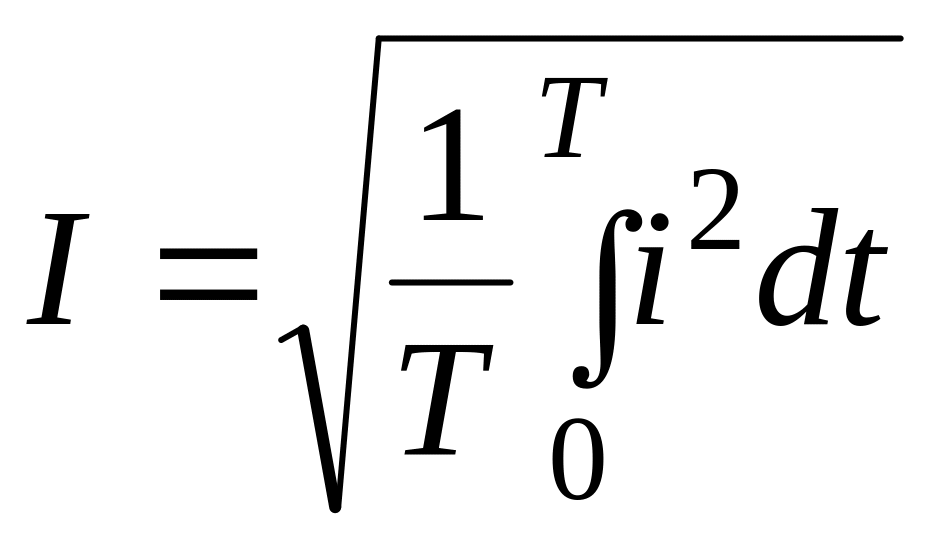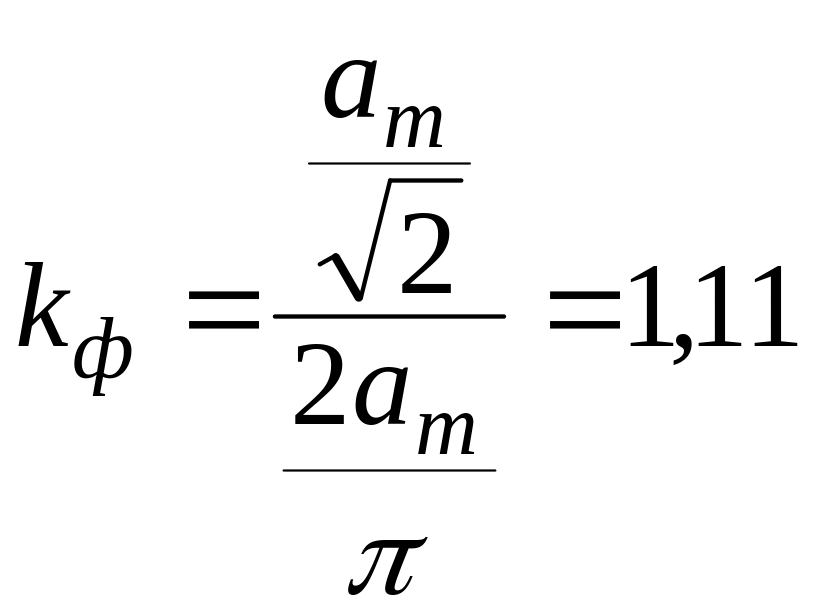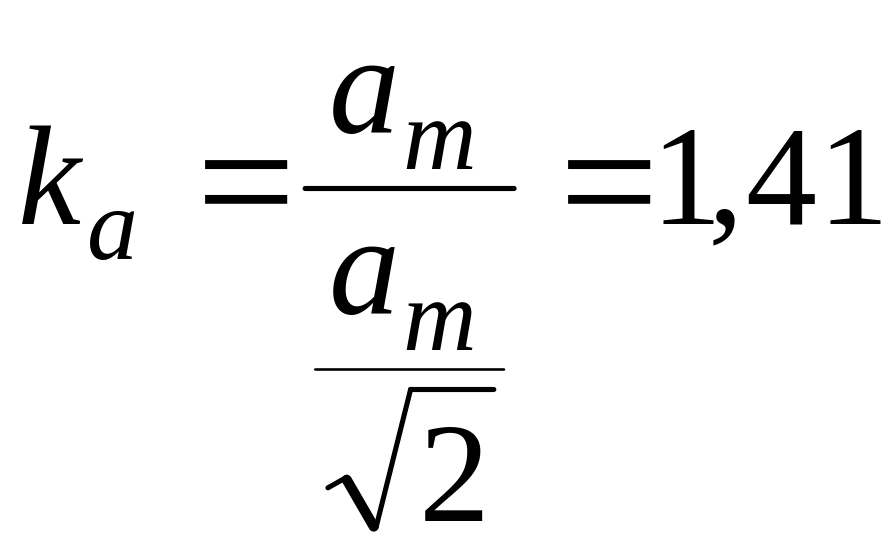