16.8. Переходный процесс в цепи с последовательно соединёнными катушкой и конденсатором

Рассмотрим случай включения последовательно соединённых катушки и конденсатора при постоянном напряжении источника питания (рис.16.12).

Тому одержимо:

;

;

.

(16.52)

З найдемо постійну інтегрування з початкових умов: у момент комутації за другим законом комутації напруга на конденсаторі дорівнює Е, тобто при t = 0 u(0) = Е і тоді рівняння (16.52) запишеться так:

,

в результаті одержимо (рис.16.11):

.

(16.53)

Знайдемо струм у колі:

.

(16.54)

Напруга на активному опорі

.

(16.55)

З енергетичної точки зору процес розрядки конденсатора характеризується переходом енергії, накопиченої в електричному полі конденсатора, у теплоту:

.

(16.56)

16.8. Перехідний процес у колі з послідовно з'єднаними котушкою і конденсатором

Розглянемо випадок включення послідовно з'єднаних котушки і конденсатора при постійній напрузі джерела живлення (рис.16.12).

Д ля послекоммутационной схемы справедливо уравнение:

или

.

(16.57)

Если продифференцировать обе части уравнения (16.57), то получим диффе­ренциальное уравнение второго порядка:

,

(16.58)

где

;

.

(16.59)

Уравнение (16.58) однородное, а это значит, что ток в данной цепи имеет только свободную составляющую.

Составляем характеристическое уравнение:

(16.60)

и находим его корни

.

(14.61)

Общее решение линейного однородного дифференциального уравнения оп­ределяется корнями. Возможны три случая.

Первый случай. Если α > ω₀, то корни p₁ и p₂ действительные и разные. При этом общее решение уравнения (14.58) запишется в виде двух экспонент:

,

(16.62)

где А₁ и А₂ – постоянные интегрирования, которые находятся из начальных усло­вий.

В момент коммутации при t = 0 ток i(0) = 0. Тогда из уравнения (16.62) имеем:

.

(16.63)

Д ля післякомутаційної схеми справедливе рівняння:

або

.

(16.57)

Якщо продиференціювати обидві частини рівняння (16.57), то одержимо диференціальне рівняння другого порядку:

,

(16.58)

де

;

.

(16.59)

Рівняння (16.58) однорідне, а це значить, що струм у даному колі має тільки вільну складову.

Складаємо характеристичне рівняння:

(16.60)

і знаходимо його корені

.

(14.61)

Загальне рішення лінійного однорідного диференціального рівняння визначається коренями. Можливі три випадки.

Перший випадок. Якщо α > ω₀, то корені p₁ і p₂ дійсні та різні. При цьому загальне рішення рівняння (14.58) запишеться у вигляді двох експонент:

,

(16.62)

де А₁ і А₂ – постійні інтегрування, які знаходяться з початкових умов.

У момент комутації при t = 0 струм i(0) = 0. Тоді з рівняння (16.62) маємо:

.

(16.63)

Из уравнения (16.57) находим значение производной в начальный момент времени, учитывая, что i(0) = 0, u_C(0) = 0:

.

(16.64)

П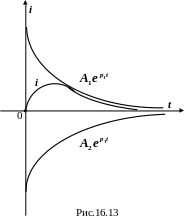 родифференцируем уравнение (16.62) и при t = 0 находим:

.

(16.65)

Совместно решая уравнения (16.63) и (16.65), имеем:

.

(16.66)

Таким образом, ток в цепи изменяется по закону (рис.16.13):

.

(16.67)

Второй случай. Если α = ω₀, то корни p₁ и p₂ действительные и одинаковые.

Общее решение уравнения (16.58) в этом случае следующее:

.

(16.68)

Постоянные интегрирования А₁ и А₂ находят из начальных условий. Форма кривой тока такая же, как и в предыдущем случае.

Третий случай. Если α < ω₀, то корни комплексно-сопряжённые:

,

(16.69)

где

.

(16.70)

З рівняння (16.57) знаходимо значення похідної в початковий момент часу, враховуючи, що i(0) = 0, u(0) = 0:

.

(16.64)

П родиференціюємо рівняння (16.62) і при t = 0 знаходимо:

.

(16.65)

Спільно вирішуючи рівняння (16.63) і (16.65), маємо:

.

(16.66)

Таким чином, струм у колі змінюється за законом (рис.16.13):

.

(16.67)

Другий випадок. Якщо α = ω₀, то корені p₁ і p₂ дійсні та однакові.

Загальне рішення рівняння (16.58) у цьому випадку наступне:

.

(16.68)

Постійні інтегрування А₁ і А₂ знаходять з початкових умов. Форма кривої струму така ж, як і в попередньому випадку.

Третій випадок. Якщо α < ω₀, то корені комплексно-спряжені:

,

(16.69)

де

.

(16.70)

Подставляя значения корней в (16.67), находим:

.

(16.71)

На рис.16.14 показан график переходного процесса в этом случае.

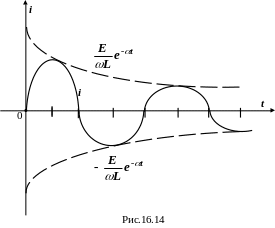
Во всех трёх рассмотренных случаях под действием источника постоянной э.д.с. происходит зарядка конденсатора. В первых двух случаях зарядный ток не изменяет своего направления, что характеризует апериодический процесс. В по­следнем случае ток представляет собой затухающую синусоиду, что характери­зует колебательный процесс. Колебания в контуре возникают вследствие перио­дического взаимного преобразования энергии электрического поля, накапливае­мой в конденсаторе, и магнитного поля катушки.

Присутствие активного сопротивления в цепи приводит к затуханию колеба­ний вследствие рассеяния энергии в активном сопротивлении. Характер про­цесса зависит от корней характеристического уравнения, которые, в свою оче­редь, определяются соотношением параметров элементов цепи.