Перехідний струм у колі

.

(16.48)

З рівняння (16.48) видно, що в момент комутації струм змінюється стрибком від нуля до значення і потім поступово зменшується.

Перехідна напруга на активному опорі

.

(16.49)

Так само як і струм, напруга на активному опорі теж змінюється стрибком від нуля до значення Е, а потім поступово зменшується.

Розглянемо енергетичний бік процесу заряджання конденсатора. Енергія, що надходить від джерела

или

,

т.е.

.

(16.50)

Таким образом, при любых значениях r и С половина энергии, полученной от источника за время переходного периода, перейдёт в теплоту на активном сопро­тивлении, а вторая половина накопится в электрическом поле конденсатора.

16.7. Разрядка конденсатора через резистор

Пусть теперь конденсатор, заряженный до напряжения Е, в момент коммута­ции замыкается на активное сопротивление (рис.16.10). Найдём закон изменения напряжения на конденсаторе в послекоммутационный период.

Д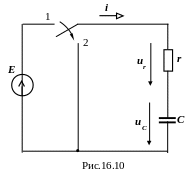 ля послекоммутационной цепи справедливы уравнения:

;
,

или

;
.	(16.51)

В данном случае переходное напряжение на конденсаторе не имеет принуж­дённой составляющей, т.е.

, поскольку .

або

,

тобто

.

(16.50)

Таким чином, при будь-яких значеннях r і С половина енергії, отриманої від джерела за час перехідного періоду, перейде в теплоту на активному опорі, а друга половина накопичиться в електричному полі конденсатора.

16.7. Розряджання конденсатора через резистор

Нехай тепер конденсатор, заряджений до напруги Е, у момент комутації замикається на активний опір (рис.16.10). Знайдемо закон зміни напруги на конденсаторі в післякомутаційний період.

Д ля післякомутаційного кола справедливі рівняння:

;
,

або

;
.	(16.51)

У даному випадку перехідна напруга на конденсаторі не має примушеної складової, тобто

, оскільки .

Поэтому получим:

;

;

.

(16.52)

Н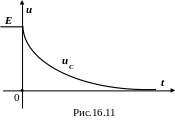 айдём постоянную интегрирования из начальных условий: в момент ком­мутации по второму закону коммутации напряжение на конденсаторе равно Е, т.е. при t = 0 u_C(0) = Е и тогда уравнение (16.52) запишется так:

,

в результате получим (рис.16.11):

.

(16.53)

Найдём ток в цепи:

.

(16.54)

Напряжение на активном сопротивлении

.

(16.55)

С энергетической точки зрения процесс разрядки конденсатора характеризу­ется переходом энергии, накопленной в электрическом поле конденсатора, в теп­лоту:

.

(16.56)
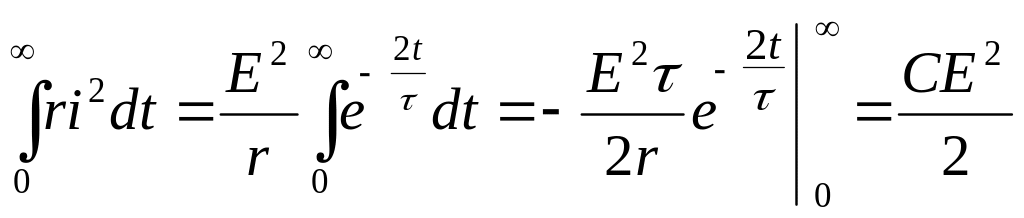