- •Тема 15 Переходные процессы в линейных цепях
- •16.1. Причины возникновения переходных процессов
- •Замыкание цепи изображают на расчётных схемах так:
- •Размыкание цепи изображают на расчётных схемах так:
- •16.2. Законы коммутации
- •Тема 16 перехідні процеси в лінійних колах
- •16.1. Причини виникнення перехідних процесів
- •Замикання кола зображують на розрахункових схемах так: Розмикання кола зображують на розрахункових схемах так:
- •16.2. Закони комутації
- •16.3. Классический метод расчёта
- •16.3. Класичний метод розрахунку
- •Отнимая почленно уравнения (16.9) и (16.10) и зная, что
- •Віднімаючи почленно рівняння (16.9) і (16.10) та знаючи, що
- •16.4. Подключение катушки к источнику постоянной э.Д.С.
- •16.4. Підключення котушки до джерела постійної е.Р.С.
- •Принуждённый ток после коммутации
- •Примушений струм після комутації
- •За время переходного периода в магнитном поле катушки накопится энергия
- •16.5. Короткое замыкание катушки
- •За час перехідного періоду в магнітному полі котушки накопичиться енергія
- •16.5. Коротке замикання котушки
- •16.6. Зарядка конденсатора через резистор
- •16.6. Заряджання конденсатора через резистор
- •Переходный ток в цепи
- •Переходное напряжение на активном сопротивлении
- •Перехідний струм у колі
- •Перехідна напруга на активному опорі
- •16.7. Разрядка конденсатора через резистор
- •16.7. Розряджання конденсатора через резистор
- •16.8. Переходный процесс в цепи с последовательно соединёнными катушкой и конденсатором
- •16.8. Перехідний процес у колі з послідовно з'єднаними котушкою і конденсатором
- •16.9. Разрядка конденсатора на катушку
- •16.9. Розряджання конденсатора на котушку
- •16.10. Включение катушки при синусоидальном напряжении
- •16.10. Включення котушки при синусоїдній напрузі
- •Для переходного тока
- •Для перехідного струму
- •16.11. Включение последовательно соединённых резистора и конденсатора при синусоидальном напряжении
- •Переходное напряжение на ёмкости
- •16.11. Включення послідовно з'єднаних резистора і конденсатора при синусоїдній напрузі
- •Перехідна напруга на ємності
- •16.12. Расчёт переходного процесса в разветвлённой цепи
- •16.12. Розрахунок перехідного процесу в розгалуженому колі
- •16.13. Преобразования Лапласа
- •16.13. Перетворення Лапласа
- •16.14. Законы Ома и Кирхгофа в операторной форме
- •16.14. Закони Ома і Кірхгофа в операторній формі
- •В знаменателе находится операторное сопротивление
- •У знаменнику знаходиться операторний опір
- •16.15. Теорема разложения
- •16.15. Теорема розкладання
- •16.16. Формула включения
- •16.16. Формула включення
- •Алгоритм изучения темы «Переходные процессы в линейных цепях»
- •16.1. Причины возникновения переходных процессов
- •16.2. Законы коммутации
- •16.3. Классический метод расчёта
- •16.4. Подключение катушки к источнику постоянной э.Д.С.
- •Алгоритм вивчення теми «перехідні процеси в лінійних колах»
- •16.1. Причини виникнення перехідних процесів
- •16.2. Закони комутації
- •16.3. Класичний метод розрахунку
- •16.4. Підключення котушки до джерела постійної е.Р.С.
- •16.5. Короткое замыкание катушки
- •16.6. Зарядка конденсатора через резистор
- •16.5. Коротке замикання котушки
- •16.6. Заряджання конденсатора через резистор
- •16.7. Разрядка конденсатора через резистор
- •16.8. Переходный процесс в цепи с последовательно соединёнными катушкой и конденсатором
- •16.7. Розряджання конденсатора через резистор
- •16.8. Перехідний процес у колі з послідовно з'єднаними котушкою і конденсатором
- •16.9. Разрядка конденсатора на катушку
- •16.10. Включение катушки при синусоидальном напряжении
- •16.9. Розряджання конденсатора на котушку
- •16.10. Включення котушки при синусоїдній напрузі
- •16.11. Включение последовательно соединённых резистора и конденсатора при синусоидальном напряжении
- •16.11. Включення послідовно з'єднаних резистора і конденсатора при синусоїдній напрузі
- •16.12. Расчёт переходного процесса в разветвлённой цепи
- •16.13. Преобразования Лапласа
- •16.14. Законы Ома и Кирхгофа в операторной форме
16.6. Зарядка конденсатора через резистор
 Рассмотрим
расчётную схему последовательного
соединения активного
сопротивления
и ёмкости, которые подключаются к
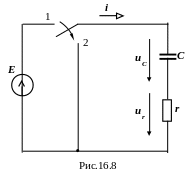
источнику постоянной э.д.с. (рис.16.8).
Рассмотрим
расчётную схему последовательного
соединения активного
сопротивления
и ёмкости, которые подключаются к
источнику постоянной э.д.с. (рис.16.8).
Найдём закон изменения напряжения на ёмкости в послекоммутационный период. Запишем для расчётной схемы уравнение по второму закону Кирхгофа:
|
(16.40) |
Учитывая, что напряжение на активном сопротивлении
|
(16.41) |
где τ = rC – постоянная времени цепи, с,
то получим дифференциальное уравнение:
|
(16.42) |
Переходное напряжение на конденсаторе
|
(16.43) |
Находим свободное напряжение на конденсаторе:
|
|
|
; |
; |
(16.44) |
|
|
|
Енергія, що виділяється в активному опорі за час перехідного процесу
. |
(16.39) |
Таким чином, WL = Wr, тобто вся енергія магнітного поля виділяється в активному опорі r у вигляді теплоти.
16.6. Заряджання конденсатора через резистор
Розглянемо розрахункову схему послідовного з'єднання активного опору і ємності, які підключаються до джерела постійної е.р.с. (рис.16.8).
Знайдемо закон зміни напруги на ємності в післякомутаційний період. Запишемо для розрахункової схеми рівняння за другим законом Кірхгофа:
. |
(16.40) |
Враховуючи, що напруга на активному опорі
, |
(16.41) |
де τ = rС – постійна часу кола, с,
то одержимо диференціальне рівняння:
. |
(16.42) |
Перехідна напруга на конденсаторі
|
(16.43) |
Знаходимо вільну напругу на конденсаторі:
|
|
|
; |
; |
(16.44) |
|
|
|
Принуждённое напряжение на конденсаторе
|
(16.45) |
Таким образом, общее решение дифференциального уравнения:
|
(16.46) |
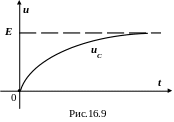
Находим постоянную интегрирования из начальных условий: в момент коммутации согласно второму закона коммутации напряжение на конденсаторе равно нулю, т.е. при t = 0 uC (0) = 0, таким образом, уравнение (16.46) для этого момента времени запишется так:
|
|
откуда
|
|
|
(16.47) |
Покажем это на графике (рис.16.9).
Переходный ток в цепи
|
(16.48) |
Из
уравнения (16.48) видно, что в момент
коммутации ток изменяется скачком
от нуля до значения
![]() и затем постепенно уменьшается.
и затем постепенно уменьшается.
Переходное напряжение на активном сопротивлении
|
(16.49) |
Так же как и ток, напряжение на активном сопротивлении тоже изменяется скачком от нуля до значения Е, а затем постепенно уменьшается.
Рассмотрим энергетическую сторону процесса зарядки конденсатора. Энергия, которая поступает от источника
|
|
Примушена напруга на конденсаторі
. |
(16.45) |
Таким чином, загальне рішення диференціального рівняння:
. |
(16.46) |
Знаходимо постійну інтегрування з початкових умов: у момент комутації відповідно до другого закону комутації напруга на конденсаторі дорівнює нулю, тобто при t = 0 u(0) = 0, таким чином, рівняння (16.46) для цього моменту часу запишеться так:
, |
|
звідки
; |
|
. |
(16.47) |
Покажемо це на графіку (рис.16.9).