16.14. Закони Ома і Кірхгофа в операторній формі

Н ехай коло (рис.16.21) підключається до джерела напруги при ненульових початкових умовах, тобто до комутації в колі проходив деякий струм. Тоді можемо записати:

i(0) ≠ 0,

uC ≠ 0.

Складемо диференціальне рівняння перехідного процесу:

,

(16.110)

де

.

(16.111)

Заменим оригиналы функций их изображениями по Лапласу (рис.16.22):

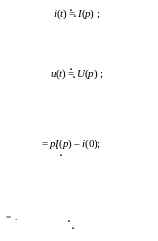
Тогда получим:

.

Отсюда

.

(16.112)

Полученное уравнение подобно закону Ома в операторной форме для пере­ходного процесса при ненулевых начальных условиях.

В знаменателе находится операторное сопротивление

.

(16.113)

Замінимо оригінали функцій їх зображеннями за Лапласом (рис.16.22):

Тоді одержимо:

.

Звідки

.

(16.112)

Отримане рівняння подібне закону Ома в операторній формі для перехідного процесу при ненульових початкових умовах.

У знаменнику знаходиться операторний опір

.

(16.113)

Оно может быть определено из комплекса полного сопротивления синусои­дального тока

путём замены jω на p.

При нулевых начальных условиях, т.е. при i(0) = 0 и u_C(0) = 0, получим:

.

(16.114)

Аналогично можно записать законы Кирхгофа в операторной форме:

;	(16.115)
.	(16.116)

16.15. Теорема разложения

В большинстве случаев изображения представляют собой полную рациональ­ную дробь:

,

(16.117)

в которой m < n, a_k и b_k – действительные числа, p₁, p₂, … p_n – корни урав­нения F(p) = 0, которые не кратны и не равны корням уравнения φ(p) = 0.

Из математики известно, что в этом случае:

= .

(16.118)

Это и есть запись теоремы разложения, которая позволяет с помощью изо­браже­ния в виде рациональной дроби найти оригинал, который равен сумме показа­тельных функций времени, умноженных на постоянные коэффициенты.

Він може бути визначений з комплексу повного опору синусоїдного струму

шляхом заміни jω на p.

При нульових початкових умовах, тобто при i(0) = 0 і u(0) = 0, одержимо:

.

(16.114)

Аналогічно можна записати закони Кірхгофа в операторній формі:

;	(16.115)
.	(16.116)
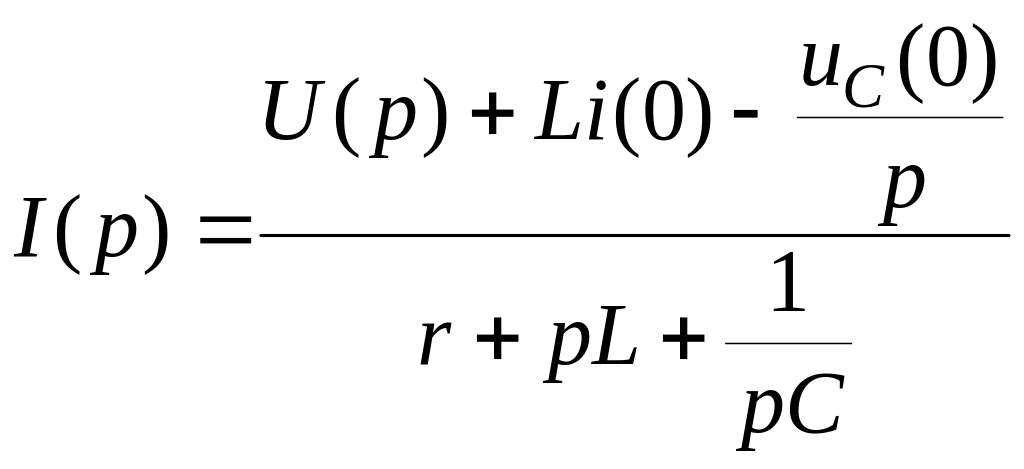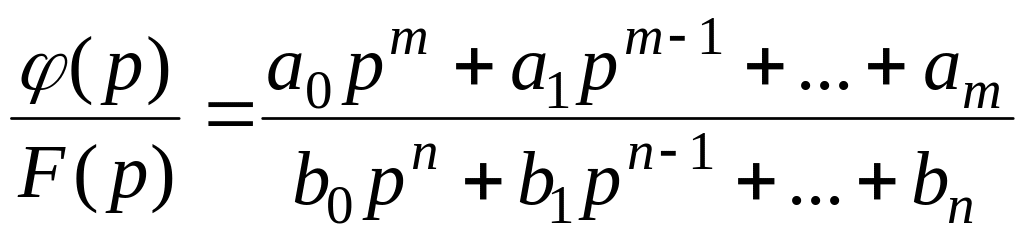