Тема 15 Переходные процессы в линейных цепях

16.1. Причины возникновения переходных процессов

До этого мы рассматривали и изучали свойства электрических цепей по­стоянного, синусоидального и периодического несинусоидального токов в уста­новившемся режиме.

В этом же разделе рассмотрим переходные процессы, под которыми будем понимать процессы перехода от одного режима работы электрической цепи к дру­гому. Они возникают вследствие включения или выключения пассивных или ак­тивных участков цепи; коротких замыканий отдельных участков цепи, разного рода переключений, внезапного изменения параметров и т.п. Все эти изменения называются коммутационными изменениями или просто коммутацией.

Замыкание цепи изображают на расчётных схемах так:

Размыкание цепи изображают на расчётных схемах так:

16.2. Законы коммутации

Б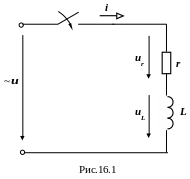 удем считать, что при замыкании и размыкании электрической цепи дуга не возникает, а коммутация проходит в момент времени t = 0.

Рассмотрим включение участка цепи с катушкой (рис.16.1).

До коммутации ток в разветвлении был равен нулю. После коммутации в соответствии со вторым законом Кирхгофа можем записать:

u = ur + uL.

(16.1)

Если предположить, что в момент коммутации (t = 0) ток изменится скачком, то u_L = ∞ и второй закон Кирхгофа не будет выполняться. Поэтому в данном слу­чае в момент коммутации сила тока равна нулю.

Тема 16 перехідні процеси в лінійних колах

16.1. Причини виникнення перехідних процесів

До цього ми розглядали і вивчали властивості електричних кіл постійного, синусоїдного і періодичного несинусоїдального струмів в усталеному режимі.

У цьому ж розділі розглянемо перехідні процеси, під якими будемо розуміти процеси переходу від одного режиму роботи електричного кола до іншого. Вони виникають внаслідок включення або вимикання пасивних або активних ділянок кола; коротких замикань окремих ділянок кола, різного роду переключень, раптової зміни параметрів і т.п. Всі ці зміни називаються комутаційними змінами або просто комутацією.

Замикання кола зображують на розрахункових схемах так: Розмикання кола зображують на розрахункових схемах так:

16.2. Закони комутації

Б удемо вважати, що при замиканні і розмиканні електричного кола дуга не виникає, а комутація проходить у момент часу t = 0.

Розглянемо включення ділянки кола з котушкою (рис.16.1).

До комутації струм у розгалуженні дорівнював нулю. Після комутації у відповідності з другим законом Кірхгофа можемо записати:

u = ur + uL.

(16.1)

Якщо припустити, що в момент комутації (t = 0) струм зміниться стрибком, то u = ∞ і другий закон Кірхгофа не буде виконуватися. Тому в даному випадку в момент комутації сила струму дорівнює нулю.

С энергетической точки зрения невозможность мгновенного изменения тока в индуктивности объясняется невозможностью изменения скачком энергии, нако­пленной в катушке. Энергия магнитного поля катушки

.

(16.2)

Мгновенная мощность в индуктивности

.

(16.3)

Если бы ток в момент времени t = 0 изменился скачком, это привело бы к вы­делению в индуктивности бесконечно большой мощности, что невозможно с фи­зической точки зрения.

Таким образом, можно сформулировать первый закон коммутации: в любом разветвлении с индуктивностью ток и магнитный поток в момент коммутации со­храняют те значения, которые они имели до коммутации, и дальше начинают из­меняться от этих значений.

Р ассмотрим теперь включение участка цепи с ёмкостью (рис.16.2).

До ком­мутации напряжение на ёмкости было равно нулю. После коммутации в соответ­ствии со вторым законом Кирхгофа можем записать:

u = ur + uС = ri + uС.

(16.4)

Из соотношений

,

(16.5)

находим

,

.

(16.6)

Если предположить, что в момент коммутации (t = 0) напряжение на ёмкости изменится скачком, то i = ∞ и второй закон Кирхгофа не будет выполняться. По­этому в данном случае в момент коммутации напряжение на ёмкости будет равно нулю.

З енергетичної точки зору неможливість миттєвої зміни струму в індуктивності пояснюється неможливістю зміни стрибком енергії, накопиченої в котушці. Енергія магнітного поля котушки

.

(16.2)

Миттєва потужність в індуктивності

.

(16.3)

Якби струм у момент часу t = 0 змінився стрибком, це привело б до виділення в індуктивності нескінченно великої потужності, що неможливо з фізичної точки зору.

Таким чином, можна сформулювати перший закон комутації: у будь-якому розгалуженні з індуктивністю струм і магнітний потік у момент комутації зберігають ті значення, які вони мали до комутації, і далі починають змінюватися від цих значень.

Р озглянемо тепер включення ділянки кола з ємністю (рис.16.2).

До комутації напруга на ємності дорівнювала нулю. Після комутації у відповідності з другим законом Кірхгофа можемо записати:

u = ur + uС = ri + uС.

(16.4)

Зі співвідношень

,

(16.5)

знаходимо

,

.

(16.6)

Якщо припустити, що в момент комутації (t = 0) напруга на ємності зміниться стрибком, то i = ∞ і другий закон Кірхгофа не буде виконуватися. Тому в даному випадку в момент комутації напруга на ємності буде дорівнювати нулю.

С энергетической точки зрения невозможность мгновенного изменения на­пряжения на ёмкости объясняется невозможностью изменения скачком мощно­сти, накопленной в конденсаторе. Энергия электрического поля конденсатора

.

(16.7)

Мгновенная мощность в ёмкости

.

(16.8)

Если бы напряжение на ёмкости в момент времени t = 0 изменилось скачком, то это привело бы к выделению в ёмкости бесконечно большой мощности, что не­возможно с физической точки зрения.

Итак, можно сформулировать второй закон коммутации: на любом участке цепи с ёмкостью напряжение и заряд на ёмкости в момент коммутации сохраняют те значения, которые они имели до коммутации, и дальше начинают изменяться от этих значений.