5.2. Математическая основа карт

5.2.1. Масштаб мелкомасштабных карт

На листе (плоскости) мелкомасштабной карты могут быть показаны большие по площади территории. Но Земля — геоид — эллипсоид вращения — шар, т. е. сфера. Поэтому при создании карты возникает задача «развернуть» сферу в плоскость с минимальными искажениями.

Если глобус Земли разрезать на любое количество долей, каждая из них будет представлять часть сферы (пусть бесконечно малую). Чтобы такую часть превратить в плоскость, придется смириться с возникновением целого ряда ошибок.

Одним из обязательных условий перехода от местности к карте является сохранение непрерывного изображения поверхности Земли.

Следовательно, чтобы часть сферы показать на плоскости, нужно либо растянуть ее по краям (полюсам) не разрывая, ли­бо сжать в центре (на экваторе), либо и то и другое одновре­менно. Растянуть — значит увеличить отрезок на карте, есте­ственно, его величина на местности останется неизменной (увеличить числитель дроби, не меняя ее знаменателя), т. е. увеличить масштаб. Сжать — значит, уменьшить масштаб. Эти операции в разных точках карты и по разным направле­ниям будут иметь неодинаковое значение. Таким образом, мы получаем в каждой точке карты свой масштаб. Он называется частным масштабом карты. Перенести на плоскость любую фигуру, полностью соответствующую фигуре на сфере, нельзя именно из-за разности в величинах частных масштабов в раз­ных частях карты.

Величина масштаба, подписанная на карте, показывает об­щую степень уменьшения модели и называется главным масштабом карты. Его величина постоянна только для опре­деленных линий (например, меридианов на карте России в проекции В. В. Красовского) или точек (например, точки пе­ресечения центрального меридиана и экватора на карте Афри­ки в проекции Ламберта), в других точках карты масштабы будут иметь другие значения (значения частных масштабов). Исходя из сказанного выше, дадим определение масштаба мелкомасштабной карты.

Масштаб мелкомасштабной карты есть отно­шение бесконечно малого отрезка на карте (точ­ки) к соответствующему ему отрезку на земной поверхности — точнее, к горизонтальной проек­ции этого же отрезка на уровенной поверхности.

• На топографической карте показан главный масштаб — средний для всего листа карты. Его значение практически одинаково в любой точке листа, поскольку ошибки в длинах линий и площа­дях на всем листе не превышают графической точности карты. Определение масштаба топографической карты по этой причине отличается от определения масштаба мелкомасштабной карты.

На мелкомасштабной карте обязательно подписывается численный масштаб (например, 1:4 000 000). Остальные виды масштабов — именованный и линейный — могут быть не по­казаны.

5.2.2. Картографические искажения

Невозможность показать на карте участок земной по­верхности без разрывов, растяжений или сжатий приводит к неравномерности одинаковых участков, расположенных в разных частях карты. Будут изменяться длины линий, пло­щади, углы, конфигурация территории.

Картографические искажения – это нарушения подобия отображенного на карте участка земной поверхности вследствие непостоянства масштабов и изменения углов между направлениями.

Искажения зависят от способа перехода от сферической по­верхности к плоскости. Величины искажений разнообразны и направлены в разные стороны, однако распределением их мож­но управлять с помощью картографической проекции.

При любом способе передачи изображения на карте будут возникать искажения. Без искажений карт не бывает.

Можно изыскать возможность уменьшить величины иска­жений или исключить их в определенной точке, на линии или системе линий, называемых точками или линиями нулевых искажений. По мере удаления от них в любом направлении ис­кажения будут возрастать. Другими словами, они увеличива­ются с увеличением картографируемой территории.

Искажения могут привести к увеличению или уменьше­нию площади или изменению формы территории, длины ли­нии, угла, т. е. в разных направлениях от точки нулевых ис­кажений знак их может изменяться. Например, по меридиану масштаб может уменьшаться, а по параллели увеличиваться.

Искажения длин, площадей и углов рассматриваются от­дельно. Для вычисления первых двух главный (общий) масштаб карты принимается за постоянное число — единицу; тогда укло­нение частного масштаба длин или площадей от единицы будет давать их относительное искажение, или просто искажение.

Искажение длин линий (µ) определяется отношением частного масштаба в точке к главному масштабу карты:

µ =

Если частный масштаб крупнее главного, то значение дро­би будет больше единицы, т. е. искажения приведут к увели­чению длины линии на карте по сравнению с этой же линией на земной поверхности. Разницу между величиной дроби и единицей можно выразить в процентах. Например, значение µ = 1,2 показывает, что линия увеличена на 0,2 (1,2 — 1) дли­ны, т. е. на 20 % . При равенстве числителя и знаменателя в ре­зультате деления получим единицу. Значит, в данной точке частный масштаб равен главному — искажение отсутствует:

Проще всего вычислять масштабы длин по главным на­правлениям, т. е. по взаимно перпендикулярным на эллипсо­иде меридианам (m) и параллелям (n).

Для примера вычислим частные масштабы m и п в севе­ро-восточном углу карты мира в атласе для 7 класса (ПКО «Картография», 2001) (рис. 39).

Следует иметь в виду, что такие вычисления не являются репрезентативными, поскольку в них нарушается главное по­нятие масштаба мелкомасштабной карты, а именно отнесение масштаба к точке. Однако они дают наглядное, хотя и грубое представление о распределении масштабов.

Широта Северного полярного круга — 66°33' (примерно, 66°,5). До следующей на карте параллели 80° остается 13°,5. На карте эта величина составляет 46 мм, на земной поверхно­сти — 1505,25 км (13°,5 х 111,5 км, где 111,5 км — длина ду­ги меридиана в 1° на широте 66°,5; см. приложение 1). Масш­таб в этом месте карты равен:

Чтобы привести числитель и знаменатель к одному изме­рению (мм), умножаем знаменатель на 10⁶. Получаем пример­но 1:32 700 000.

Главный масштаб выбранной нами карты 1:75 000 000. Обозначать частные масштабы длин по меридианам принято буквой т, а по параллелям — п. Следовательно, величина ча­стного масштаба по меридиану в данной точке по отношению к главному т = 1/32 700 000:1/75 000 000 = 2,4.

Это значит, что в данном месте карты частный масштаб по меридиану в 2,4 раза крупнее главного.

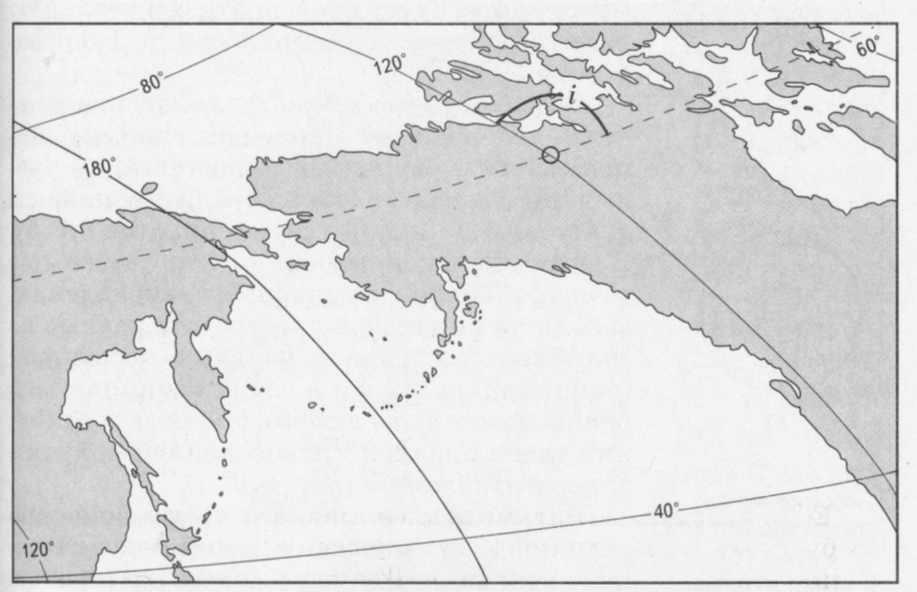
Рис. 39. Фрагмент карты мира из атласа 7 класса

Вычислим частный масштаб по параллели (n) в этом же месте карты. Длина дуги Северного полярного круга между 180° и 120° з. д. составляет 48 мм на карте и 2670 км на зем­ной поверхности (длина дуги одного градуса параллели на ши­роте 66°,5 = 44,5 км). Частный масштаб по параллели

Получим примерно величину масштаба 1:55 600 000. Следовательно, частный масш­таб по параллели в долях главного в этом месте карты составляет:

п = 1/55 600 000 : 1/75 000 000, что при­мерно равно 1,3.

Значит, длина отрезка параллели в этом месте карты будет превышать его реальную длину на земной поверхности в 1,3 раза, т. е. на 30 % .

В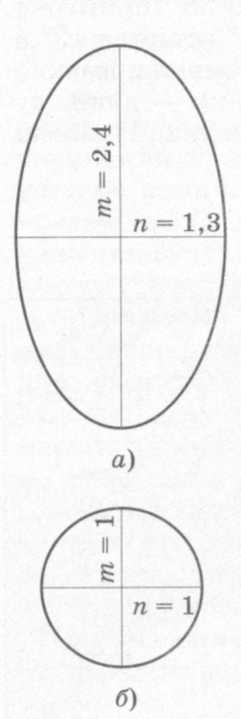 любой точке земного эллипсоида име­ются два взаимно перпендикулярных на­правления — меридиан и параллель (в предыдущем примере мы выбрали меридиан с долготой 120° и параллель с широтой 66°,5). В ортогональной проекции это также два взаимно перпендикулярных направления. И если на них отложить отрезки, равные по величине полученным частным масштабам (например, т = 2,4 и п = 1,3, единица изме­рения может быть любой), то после соедине­ния точек плавной кривой линией получим эллипс искажений (рис. 40, а).

Э

Рис. 40. Эллипс искажений (а) превращается в круг (б) в точке нулевых искажений

ллипс искажений дает представление о величинах искажений и распределении их на карте. Такие эллипсы можно построить в любой части карты. Из-за разности в величинах частных масштабов формы и размеры их будут раз­личны.

В точках нулевых искажений, где частные масштабы по меридиану и параллели равны главному масштабу, т. е. еди­нице, эллипс превратится в круг (рис. 40, б).

Искажение угла (ω) — разность между углом, образован­ным двумя направлениями на эллипсоиде, и этим же углом на карте. Для определения величины искажения можно срав­нить угол в точке между меридианами и параллелями на кар­те (i) и тот же угол на земной поверхности, всегда равный 90°; ω = i - 90°. Искажения углов могут иметь различную величину. Например, на карте полушарий в точке пересечения эквато­ра и центрального меридиана оно равно 0°, на карте мира в точке пересечения Северного полярного круга и меридиана 120° з. д. ω = 30° (см. рис. 41).

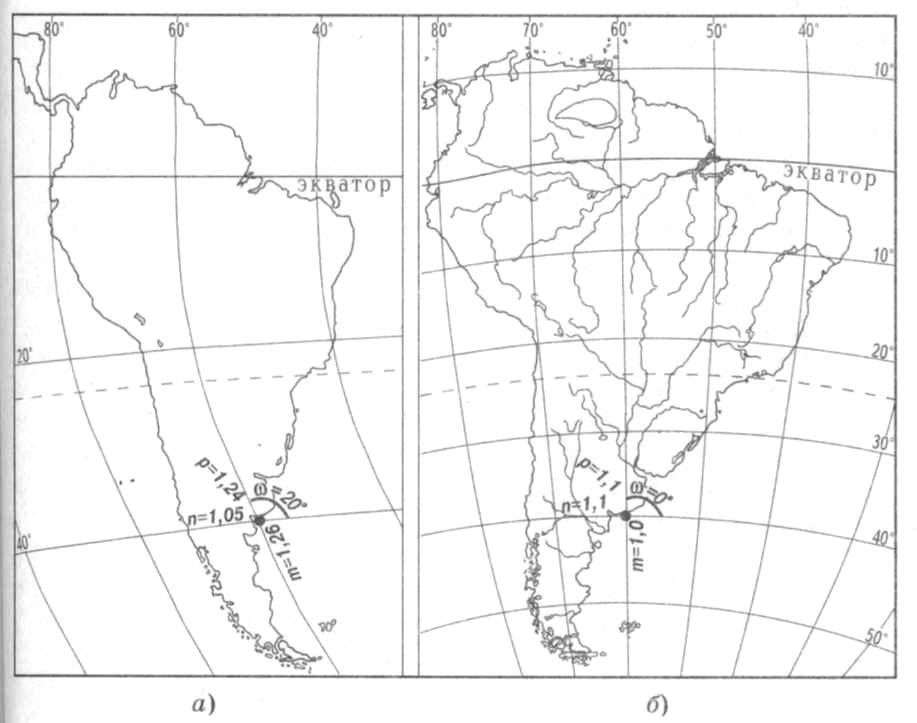
Рис. 41. Изменение вида экватора и формы территории вследствие искажений углов и длин линий по разным направлениям

Искажения в длинах линий и углах приводят к искажени­ям конфигурации территории (рис. 6.3, а, б). Круг на поверх­ности Земли может изобразиться кругом на карте только в точ­ках или на линиях нулевых искажений. В общем случае на карте он изображается эллипсом.

Величина искажения площади выражается разностью между площадями бесконечно малого эллипса на карте и соот­ветствующего ему круга на поверхности Земли. Частный масш­таб площади в данной точке (р) вычисляется через частные масштабы длин m и n и искажение углов ω:

р = m· n · cos ω

Если в точке карты отсутствуют искажения в длинах ли­ний, т, е. m = n = 1 и угол между меридианами и параллелями равен 90° (ω= 0°, cos 0° = 1), то масштаб площади р = 1. Следо­вательно, в данной точке масштаб площади равен главному масштабу карты.

Проекций, совершенно лишенных искажений длин линий, не существует. Вместе с тем разработаны проекции, свободные от искажения углов и площадей. При искажении длин линий по разным направлениям и углов между ними исказятся фор­мы территорий, но могут сохраниться их площади. Величины искажений можно определить на глаз по величине и форме трапеций географической сетки в одном широтном поясе. На рис. 42 дан вид трапеций, образованных на карте Евразии ме­ридианами и параллелями в широтном поясе 50—60° с. ш.

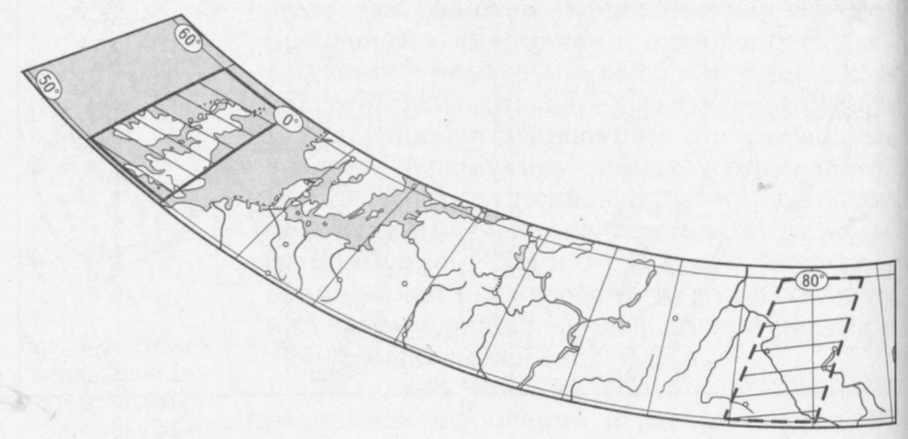
Рис. 42. Сравнение формы и площади трапеции картографической сетки в разных частях карты Евразии (фрагмент)

Для изучения характера распределения искажений в раз­ных точках карты вычисляют частные масштабы длин линий и площадей и искажения углов. Точки с одинаковыми зна­чениями соединяют линиями, которые называются изоколами — линиями равных искажений. Изучают раздельно изоколы масштабов длин, изоколы масштабов площадей и изоко-лы искажений углов. Вид изокол зависит от картографической проекции, в которой составлялась карта (рис. 43).