III. Транспортная задача линейного программирования в задачах связи

3.1. Определение транспортной задачи

Транспортная задача линейного программирования формулирует­ся следующим образом.

Имеется m пунктов отправления (ПО): A₁, A₂, …, A_m, в ко­торых сосредоточены запасы какого-то однородного груза в количест­ве соответственно a₁, a₂, …, a_m единиц. Кроме того, имеется пунктов назначения (ПН): B₁, B₂, …, B_n подавших заявки соот­ветственно на b₁, b₂, …, b_n, единиц груза.

Предполагается, что сумма всех заявок равна сумме всех запа­сов:

a_i = b_j (3.1)

Известна стоимость С_ij перевозки единицы груза от каждого пункта отправления A_i до каждого пункта назначения В_j. Таблица (матрица) стоимостей перевозки С_ij задана:

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех пере­возок была минимальна.

При такой постановке задачи показателем эффективности плана перевозок является стоимость; поэтому поставленную задачу точнее называют транспортной задачей по критерию стоимости.

Дадим этой задаче математическую формулировку. Обозначим x_ij- количество груза, отправляемого из i-го пункта отправле­ния в j-й пункт назначения B_j .

Неотрицательные переменные, число которых равно m*n, должны удовлетворять следующим ус­ловиям.

I. Суммарное количество груза, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте. Это дает т условий-равенств:

x_1j =a₁,

x_2j =a₂, (3.2)

………….

x_mj =a_m,

2. Суммарное количество груза, доставляемое в каждый пункт назначения изо всех пунктов отправления, должно быть равно заяв­ке, поданной данным пунктом. Это дает n условий-равенств:

x_i1=b₁,

x_i2=b₂, (3.3)

…………

x_in=b_n,

Условия (3.2), (3.3) называются "балансовыми условиями".

3. Суммарная стоимость всех перевозок, т.е. сумма величин x_ij, умноженных на соответствующие стоимости С_ij, должна быть минимальной:

L= С_ij x_ij = min (3.4)

Функции (3.4), являющаяся целевой функцией линейна, ограни­чения-равенства (3.2), (3.3) также линейны. Перед нами – типичная задача линейного программирования с ограничениями - равенствами, называемая основной задачей линейного программирования (ОЗЛП).

Данная задача имеет некоторые особенности, позволяющие ре­ шить ее вручную простыми табличными методами. Во-первых, все коэффициенты при переменных в уравнениях (3.2), (3.3) равны едини­це. Во-вторых, не все m+n уравнений задачи являются независимыми. Действительно, складывая между собой все уравнения (3.2) и все уравнения (3.3), мы должны получить одно и то же в силу условия (3.1). Таким образом, условия (3.2), (3.3) связаны одной линейной зависимостью и фактически из этих уравнений только m , а не n являются линейно независимыми. Значит, ранг r системы уравнений (3.2), (3.3) равен

r=m+n-1

а, следовательно, можно разрешить эти уравнения относительно m+n-1 базисных переменных, выразив их через остальные, свобод­ные, количество которых равно

K=mn-(m+n-1) = (m-1) (n-1)

Как известно, в задаче линейного программирования оптималь­ное решение достигается в одной из вершин области допустимых ре­шений (ОДР), где, по крайней мере, K переменных обращаются в нуль. Значит, в нашем случае для оптимального плана перевозок, по край­ней мере (m-1)(n-1) значений x_ij должны быть равны нулю.

Условимся о терминологии. Значения x_ij количества единиц груза, направляемых из пункта A_i в пункт B_j, будем называть перевозками.

Любую совокупность значений x_ij (i=1,m; j=1,k) будем на­зывать планом перевозок или просто планом.

План x_ij будем называть допустимым, если он удовлетворяет условиям (3.2), (3.3): все заявки удовлетворены, все запасы исчерпаны.

Допустимый план будем называть опорным, если в нем отличны от нуля не более r=m+n-1 базисных перевозок x_ij, а остальные перевозки равны нулю.

План x_ij будем называть оптимальным, если он, среди всех допустимых планов, приводит к наименьшей стоимости всех перевозок.

Перейдем к изложению табличных методов решения транспортной задачи (ТЗ), которые сводятся к более простым операциям с так на­зываемой транспортной таблицей, где в определенном порядке записаны все исходные условия ТЗ.

Образец транспортной таблицы дан в табл. 3.1, где стоимости перевозок единицы груза из ПО A_i в ПН B_j помещаются в правом верхнем углу каждой клетки таблицы, о тем, чтобы в самой клетке при составлении плана помещать перевозки x_ij.

Таблица 3.1

ПО ПН	B1	B2	…	Bn	Запасы
A1	C11	C12	…	C1n	a1
A2	C21	C22	…	C2n	a2
	…	…	…	…
Am	Cm1	Cm2	…	Cmn	a
заявки	b1	b2	…	bn	ai bj

В правом столбце помещены запасы товара в каждом ПО, в ниж­ней строке - заявки, поданные каждым ПН. В правой нижней клетке таблицы записывается сумма запасов, равная сумме заявок.

Как показано выше, в каждом опорном плане, включая оптималь­ный, будут отличны от нуля не более чем m+n-1 перевозок. Клетки таблицы, в которых записываются эти отличные от нуля пере­возки, условимся называть базисными, а остальные (пус­тые) - свободными.

Таким образом, решение ТЗ свелось к следующему. Найти такие значения положительных перевозок, которые, будучи проставлены в базисных клетках транспортной таблицы, удовлетворяли бы следую­щим условиям:

- сумма перевозок в каждой отроке таблицы должна быть равна запасу данного ПО;

- сумма перевозок в каждом столбце должна быть равна заявке данного ПН;

- общая стоимость перевозок - минимальная.

В дальнейшем все действия по нахождению решения ТЗ будут сводиться к преобразованию транспортной табл. 3.1. При описании этих преобразований будем пользоваться нумерацией клеток таблицы, подобной нумерации клеток шахматной доски. Клеткой A_iB_j или, короче, клеткой (i, j) будем называть клетку, стоящую в i-й строке и j-м столбце транспортной таблицы.

Решение транспортной задачи, как и воякой задачи линейного программирования, начинается о нахождения опорного решения (опор­ного плана). Существуют различные способы построения опорного плана, из которых мы остановимся на простейшем, так называемом "способе северо-западного угла". Пояснить его проще всего будет на конкретном примере.

Пример 1. Условия ТЗ заданы транспортной табл. 3.2.

2. Требуется найти опорное решение ТЗ (построить опорный план).

Решение. Будем заполнять табл.3.2 перевозками постепенно, начиная с левой верхней клетки (1,1) ("северо-западного угла" таблицы). Будем рассуждать при этом следующим образом. Пункт подал заявку на 18 единиц груза. Удовлетворим эту заявку за счет запаса 48, имеющегося в пункте A₁, и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В₁, удовлетворена, а в пункте A₁ осталось еще 30 единиц груза. Удовлетворим за счет их заявку пункта В₂ (27 единиц), запишем 27 в клетку (1,2); оставшиеся 3 единицы груза пункта A₁ назначим пункту B₃. В составе заявки пункта B₃ остались неудовлетворенными 39 единиц. Из них 30 покроем за счет пункта A₂, чем его запас будет ис­черпан, и еще 9 возьмем из пункта А₃.

Таблица 3.2

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	10	8	5	6	9	48
A2	6	7	8	6	5	30
A3	8	7	10	8	7	27
A4	9	5	4	6	8	20
Заявки bj	18	27	42	12	26	125

Из оставшихся 18 единиц пункта A₃ 12 выделим пункту B₄; ос­тавшиеся 6 единиц назначим пункту B₅, что вместе со всеми 20 единицами пункта A₄ покроет его заявку (табл.3.3).

Таблица 3.3

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	18 10	27 8	3 5	6	9	48
A2	6	7	30 8	6	5	30
A3	8	7	9 10	12 8	6 7	27
A4	9	5	4	6	20 8	20
Заявки bj	18	27	42	12	26	125

На этом распределение запасов закончено: каждый пункт назна­чения получил груз согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запа­су, а в столбце - заявке.

Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является не только допустимым; но и опорным решением транспортной задачи. Действительно, число базисных клеток таблицы, в которых стоят ненуле­вые перевозки, удовлетворяет условию m+n-1=8. Остальные клетки - свободные (пустые), в них стоят нулевые перевозки и их число равно 12. Значит, наш план - опорный и по­ставленная задача построения опорного плана решена.

Однако полученный опорный план не является оптимальным, по­скольку при его построении мы совсем не учитывали стоимостей пе­ревозок С_ij. Стоимость этого плана, которая найдется, если умножить каждую перевозку на соответствующую стоимость, равна

18.10+ 27.8 + 3.5 + 30.8 + 9.10 + 12.8 + 6.7 + 20.8 = 1039.

Прежде чем рассматривать способы улучшения опорного плана и обеспечения его оптимальности, опишем еще один способ нахожде­ния опорного плана называемый способом "минимальных стоимостей перевозок". В этом случае в матрице стоимостей перевозки (матрице затрат) отыскиваем минимальный элемент и в первую очередь включа­ем в план самую дешевую перевозку, притом в максимально возмож­ном объеме. Обращаясь к исходным данным табл.3.2, в план включаем перевозку 20 единиц груза из ПО А₄ в ПН B₄ со стоимостью 4, что полностью исчерпывает запас ПО A₄. Следующий по величине элемент матрицы затрат (5), расположенный в нескольких клетках таблицы, определяет включение в план перевозки между пунктами A₂ и B₅ , где объем перевозки наибольший (26), и затем перевозки между пунктами A₁ и В₃ объемом 22 единицы, что удовлетворяет заяв­ки пунктов B₃, и В₅. Далее планируются перевозки со стоимостью 6 между пунктами A₁ и B₄ объемом 15 единиц и пунктами A₂ и B₁ объемом 4 единицы. Продолжая действовать аналогичным образом и дальше, придем к плану перевозок табл.3.4.

В том, что полученный план перевозок допустимый, легко убе­диться, проверив, что суммы элементов в каждой отроке табл. 3.4 равны соответствующим запасам, а суммы по столбцам - заявкам. По­скольку число базисных (ненулевых) клеток равно m+n-1=8, а число свободных (нулевых) равно (n-1)(m-1)=12, где m=4, n=5, построенный план перевозок является не только допустимым, но и опорным. Затраты на реализацию этого плана составляют

11.10 + 4.6 + 3.8 + 24.7 + 22.5 + 2074 + 26.5 = 736.

Таблица 3.4

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	11 10	8	22 5	15 6	9	48
A2	4 6	7	8	6	26 5	30
A3	3 8	24 7	10	8	7	27
A4	9	5	20 4	6	8	20
Заявки bj	18	24	42	15	26	125

Рассмотренный способ построения опорного плана прост, но в ряде случаев приводит к опорному" решению, которое значительно от­личается от оптимального. Лучшего результата можно добиться c по­мощью метода наименьшей стоимости. Из всех цен за единицу перевоз­ки выбираем наименьшую – 4 (A₄-B₃). В эту клетку включаем максимально возможную перевозку из пункта A₄- 20. Во всех ос­тальных клетках этой отроки будут нули, т.к. в пункте A₄ ниче­го не осталось. Пункт B₃ нуждается в 42 ед., 20 он уже получил. В этом столбце следующая минимальная стоимость перевозки – 5(A₁-B₃). В это место нужно поставить недостающее количество груза (22), поставив в остальных клетках этого столбца нули. Продолжая в этом же духе, получим следующую таблицу.

Таблица 3.5

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	0	14	22	12	0	48
A2	4	0	0	0	26	30
A3	14	13	0	0	0	27
A4	0	0	20	0	0	20
Заявки bj	18	27	42	12	26	125

3.2. Решение транспортной задачи методом потенциалов

Описанный выше распределительный метод решений транспортной задачи обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. Существует, однако, специальный метод решения, который позволяет автоматически, без размышления выделять свободные клетки с отрицательной ценой цикла и определять их цены. Это так называемый метод потенциалов. В соответ­ствии c этим методом критерий оптимальности плана формулируется следующим образом.

Допустимый план перевозок тогда и только тогда является оп­тимальным, когда каждому пункту отправления и назначения можно со­поставить величину, характеризующую уровень оценки груза в нем (потенциал) так, что множество этих потенциалов удовлетворяет сле­дующим условиям.

1. Разность потенциалов пунктов назначения и отправления, между которыми запланированы перевозки, равна затратам по транспорти­ровке единицы груза между этими пунктами.

2. Аналогичные разности для всех остальных пар пунктов, между которыми не запланированы перевозки, не превосходят затрат по транспортировке.

Иначе говоря, если обозначить через U_i потенциал для i-го пункта отправления, а через V_j - для j-го пункта назначения, то эти условия запишутся так:

V_j- U_i ≤ С_ij

причем V_j- U_i ≤ С_ij, если перевозка из пункта A_i в пункт B_j предусмотрена в плане (x_ij>0).

В транспортной задаче оценки (потенциалы) имеют прозрачный экономический смысл. Они выступают здесь как локальные (поясные) цены (или наценки к единой цене), создающие заинтересованность в правильном направлении перевозок. При такой интерпретации при­знак оптимальности плана представляет собой, по сути, математичес­кое выражение здравого смысла: если какая-то перевозка осуществ­ляется, то цена в пункте потребления равна цене в пункте произ­водства плюс транспортные затраты; в остальных случаях цена V_j не может быть больше, чем U_i +С_ij, так как продукт в пункте B_j по такой цене можно было бы получить, привезя его с затратами из пункта A_i. Следовательно, V_j≤U_i +С_ij , т.е. в обоих указанных случаях разность цен не превышает затрат по перевозке.

С помощью критерия оптимальности можно не только проверить на оптимальность любой план, но и, в случае его неоптимальности, указать способ улучшения этого плана. Приведем пример построения оптимального плана о помощью последовательного улучшения, исходя из некоторого исходного допустимого плана, например, приведенного в табл. 3.4 опорного плана. Для того чтобы проверить план табл.3.4 на оптимальность, прежде всего, вычисляем систему потенциалов (оце­нок единицы продукта) в пунктах отправления и пунктах назначения. Так как потенциалы определяются c точностью до постоянного слагае­мого (важно соотношение между потенциалами, а не их абсолютная ве­личина), какой-нибудь из них можем ведать заранее. Пусть, например, U₁=10, причем через U обозначим потенциалы пунктов отправления, а через V - назначения. Используя тот факт, что разность потен­циалов между пунктами назначения и отправления, ввязанными в пла­не перевозками (см. табл. 3.4), равны соответствующим транспортным затратам, один за другим находим остальные потенциалы:

U₁=10,

V₁= U₁+C₁₁=10+10=20, U₃= V₁-C₃₁=20-8=12,

V₃= U₁+C₁₃=10+5=15, U₄= V₃-C₄₃=15-4=11,

V₄= U₁+C₁₄=10+6=16, V₂= U₃+C₃₂=12+7=19,

U₂= V₁-C₂₁= 20-6= 14 V₅= U₂+C₂₅=14+5=19

Теперь проверим выполнение признака оптимальности. Для этого нужно согласно условию 2 подсчитать величины V_j- U_i -С_ij. Если они все ≤0, то план оптимален, иначе план может быть улучшен.

Находим:

V₁-U₄-C₄₁=10-11-7=-8; V₄-U₂-C₂₄=16-14-6=-4;

V₂-U₁-C₁₂=19-10-8=1; V₄-U₃-C₃₄=16-12-8=-4;

V₂-U₂-C₂₂=19-14-7=-2; V₄-U₄-C₄₄=16-11-6=-1;

V₂-U₄-C₄₂=19-11-5=3; V₅-U₁-C₁₅=19-10-9=0;

V₃-U₂-C₂₃=15-14-8=-7; V₅-U₃-C₃₅=19-12-7=0;

V₃-U₃-C₃₃=15-12-10=-7; V₅-U₄-C₄₅=19-11-8=0.

Для пунктов, между которыми предусмотрены перевозки, эти раз­ности, очевидно, равны нулю и поэтому не выписываются. Так как не­которые из найденных значений разностей положительны, то план не оптимален. Что бы его улучшить, введем в план перевозку в объеме K между пунктами А₄ и В₂, для которых соответствующая раз­ность положительна и максимальна по величине. Однако введение до­бавочной перевозки нарушает сбалансированность плана (объем вво­за в пункт В₂, не соответствует его заявке или объем вывоза из пункта А₄ - его запасу), поэтому необходимо одновременно изме­нить объемы перевозок и между некоторыми другими пунктами.

В табл.3.6 приведен план, содержащий все необходимые изменения в объ­емах перевозок.

Таблица 3.6

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	11-K 10	8	22+K 5	15 6	9	48
A2	4 6	7	8	6	26 5	30
A3	3+K 8	24-K 7	10	8	7	27
A4	9	K 5	20-K 4	6	8	20
Заявки bj	18	24	42	15	26	125

Нетрудно проверить, что этот план сбалансирован - из каждого пункта вывозится столько, сколько в нем запасено, а каждый пункт назначения получает столько, какова его заявка. Легко убедиться, что затраты по реализации этого плана перевозок меньше первона­чальных на величину

(V₂-U₄-C₄₂ )K=3K. Действительно, эти за­траты равны

L= (11-K)C₁₁+(22+K)C₁₃+15C₁₄+4C₂₁+26C₂₅+(3+K)C₃₁+(24-K)C₃₂+KC₄₂+

+ (20-K) C₄₃=L_пп- (C₁₁-C₁₃+C₃₂-C₃₁+C₄₃-C₄₂

где L_пп - стоимость прежнего плана. С другой стороны, из соотно­шений

V₂= U₃+C₃₂, U₃= V₁-C₃₁, V₁= U₁+C₁₁, U₄= V₃-C₄₃, V₃= U₁+C₁₃ следует, что

(V₂-U₄-C₄₂) =C₁₁-C₁₃+C₃₂-C₃₁+C₄₃-C₄₂, что и доказывает вышеприведенное утверждение. Следовательно, выгодно К вы­брать как можно большим. Поскольку объемы перевозок не могут быть отрицательными, наибольшее возможное значение К равно 11. Пола­гая К=11, находим новый допустимый и опорный экономически бо­лее выгодный план, приведенный в табл.3.7.

Таблица 3.7

ПО ПН	B1	B2	B3	B4	B5	Запасы
A1	10	8	33 5	15 6	9	48
A2	4 6	7	8	6	26 5	30
A3	14 8	13 7	10	8	7	27
A4	9	11 5	9 4	6	8	20
Заявки bj	18	24	42	15	26	125

Нахождением нового опорного плана заканчивается первое при­ближение. Дальше проведенные операции повторяются снова, но уже для нового плана. Прежде всего, вычисляются потенциалы и проверя­ются условия оптимальности. Если они выполнены, то решение закон­чено. Если нет, то снова производится переход к лучшему плану и т.д.

3.3. Частные случаи транспортной задачи

В рассмотренных выше случаях число заявок равнялось числу запасов. Чаще всего бывает не так.

1) Число запасов превышает число заявок. В этом случае необ­ходимо ввести дополнительный фиктивный пункт потребления с нуле­выми стоимостями перевозок (т.е. везти никуда не надо). Далее за­дача решается обычным способом, но часть запасов окажется не вос­требованной.

2) Число заявок превышает число запасов. В этом случае вво­дится фиктивный пункт производства с нулевыми стоимостями перевоз­ки. Задача решается также обычно, только некоторые пункты потребления не дополучат требуемое, но стоимость всей операции все равно получится минимальной.

3.4. Случаи вырождения и способы их преодоления

Выше отмечалось, что число занятых мест в таблице должно быть равно m+n-1. Однако на практике встречаются случаи, ког­да в процессе решения оно сокращается. Это явление называется вы­рождением. Рассмотрим это на примере, в табл. 3.8 имеется свободное место 12. Воспользуемся им для улучшения решениям.

Таблица 3.8

ПО	ПН
	1	2	3	4
I	30 1	+    -  1	0 1.2	3
II	0.8	3  -    + 50	90 1.3	20 0.9
III	4	2.6	1.8	30 1.3

При вычитании 50 из клеток П.2 и 1.3 значения их превращаются в 0. В результате сокращается число занятых клеток и невозмож­но воспользоваться методом потенциалов.

Для преодоления этого в одну из освободившихся клеток поста­вим 0 и будем считать эту клетку занятой (табл. 3.9). Число занятых мест в таблице равно 6 (т.е. m+n-1).

Иногда приходится встречаться о вырождением уже при составле­нии исходного решения. Вырождения в этом случае можно избежать, пе­реставляя местами столбцы или строки.

Транспортная задача может использоваться в различных сферах хозяйства связи. Ниже приведены два примера.

Таблица 3.8

ПО	ПН
	1	2	3	4
I	3 -    +  0 1	5  +   0 1   -	0 1.2	3
II	0.8	3 	90 1.3	20 0.9
III	4	2.6	1.8	30 1.3

Пример 1. Газеты поступают на четыре вокзала города в количествах a₁, a₂, a₃, a₄. Нужно развести их по 4 отделениям связи в количествах b₁, b₂, b₃, b₄:

a₁=120, a₂=144, a₃=168, a₄=192,

b₁= 96, b₂=168, b₃=120, b₄=192.

Расстояние от вокзалов до отделений связи приведены в таблице. Оставшиеся Газеты реализуют на вокзале. Составить оптимальный план перевозок.

Таблица 3.10

bj ai	b1	b2	b3	b4
a1	7.2	11.7	10.8	17.1
a2	9.9	6.3	5.4	12.6
a3	8.1	11.7	3.6	9.9
a4	14.4	15.3	16.2	2.7

Пример 2. Распределить емкость трех АТС (5000, 7000, 10000) между четырьмя районами с потребностями 7000, 7000, 6000, 5000 так, чтобы обеспечить минимальный расход кабеля. Расстояние между районами и АТС приведены в таблице.

Таблица 3.11

р-ны АТС	1	2	3	4
1	1.2	0.8	1.3	1.0
2	0.7	0.9	1.1	0.8
3	0.5	1.0	0.8	0.6

3.5. Метод Фогеля

Метод Фогеля применяется для построения опорного плана. В большинстве случаев этот способ дает опорный план, наиболее близ­кий к оптимальному. Использовать этот метод рекомендуется при расчетах вручную.

В основе метода лежит концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных расходов мар­шрута.

Алгоритм метода включает следующие основные этапы.

Таблица 3.12

	B1	B2	B3	B4	ai	Столбцы разностей
A1	70	38	14 24	92	14	14	-	-	-	-
A2	58	20 18	56	72	20	38	-	-	-	-
A3	23 19	2 10	1 100	30	26	9	9	9	11	81
A4	7 3	36	121	34 8	41	5	5	5	5	118
bj	30	22	15	34
Строки разностей	16	8	32	22
	16	26	76	22
	16	26	21	22
	16	-	21	22
	16	-	21	-

1. Вычисление разностей в каждой отроке и в каждом столбце матрицы между наименьшей стоимостью и ближайшей к ней по величи­не (табл.3.12). Разности по строкам записываются справа в столбце разностей, разности по столбцам - внизу в строке разностей. Напри­мер, для строки A₁ разность равна A₁B₂- A₁B₃ =38-24=14 и т.д.

2. Поиск из всех разностей, как по строкам, так и по столбцам максимальной. В примере эта разность равна 38.

3. Помещение в клетку, где находится наименьшая стоимость пе­ревозки (A₂B₂ =18) в отроке о наибольшей разностью максимально возможного количества ресурсов (20). Поскольку при этом все ресур­сы отправителя A₂ исчерпаны эту отроку из дальнейшего рассмотре­ния исключаем.

4. Вычисление разностей по столбцам и отрокам, не принимая во внимание стоимости в клетках, имеющих ресурсы, и клетках исклю­ченной строки, и определение максимальной разности в строке или столбце (B₃=76).

5. Поиск минимального элемента в строке или столбце с максимальной разностью A₁B₃ =24 и размещение в данную клетку максимально возможного количества ресурса. Затем возвращаемся к этапу 4.

Окончательное значение целевой функции F=1546.

3.6. Транспортная задача с промежуточными пунктами

В этом случае допускается "перевозка груза" и через другие исходные пункты транзитом прежде, чем они достигнут установленного пункта назначения. Каждую вершину транспортной сети (как исходный пункт, так и пункт назначения) можно рассматривать и как исходный пункт и как пункт назначения.

Д ля пояснения этого рассмотрим задачу на примере. Имеются три завода по производству связного оборудования и два центра его распределения (A, B, С и 1, 2). В модели с промежуточными пунктами будет пять исходных пунктов и пять пунктов назначения. На рис. 3.1 изображена соответствующая сеть. Для того чтобы учесть транзитные перевозки, в каждом исходном пункте назначения предусматривается буфер емкостью D (буфер - это своего рода склад, емкость которого должна быть не меньше суммарного объема произ­водства). Предположим, что объемы производства составляют А- 1000 ед., B- 1500 ед., С- 1200 ед., тогда емкость буфера соста­вит 3700 ед.

Рис. 3.1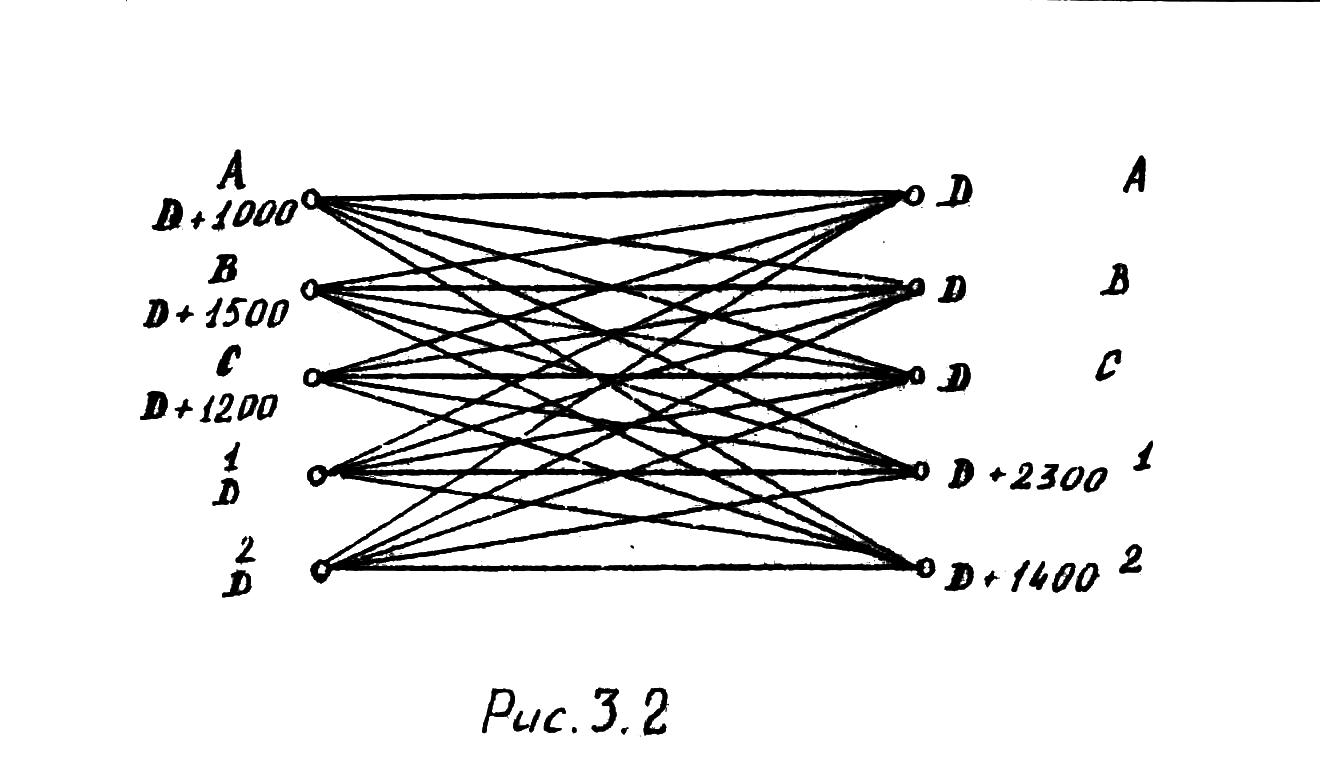

Таблица 3.13

	A	B	C	1	2
A	3700 0	130	90	1000 80	215	4700
B	135	3700 0	200 101	1300 100	108	5200
C	95	105	3500 0	102	1400 68	4900
1	79	99	110	3700 0	205	3700
2	200	107	72	205	3700 0	3700
	3700	3700	3700	6000	5100

В табл. 3.13 представлено оптимальное решение рассмотренной за­дачи. Диагональные элементы получены в результате использования бу­фера. Они не дают никакой информации об окончательном решении. На рис. 3.2 приведена схема окончательного решения.

Помимо рассмотренной выше ситуации могут быть и более сложные варианты. Например, кроме двух центров распределения продукции имеется пять потребителей (3, 4, 5, б, 7). Спрос у потребителей характеризуется следующими цифрами: 600, 500, 750, 1000, 650 ед. В такой ситуации, как показано на рис. 3.3, промежуточными пункта­ми могут быть только центры распределения. Построенная c учетом этого модель приведена в табл. 3.14. Заштрихованные клетки говорят о том, что перевозки c завода непосредственно потребителю не предусмотрены.

Рис. 3.2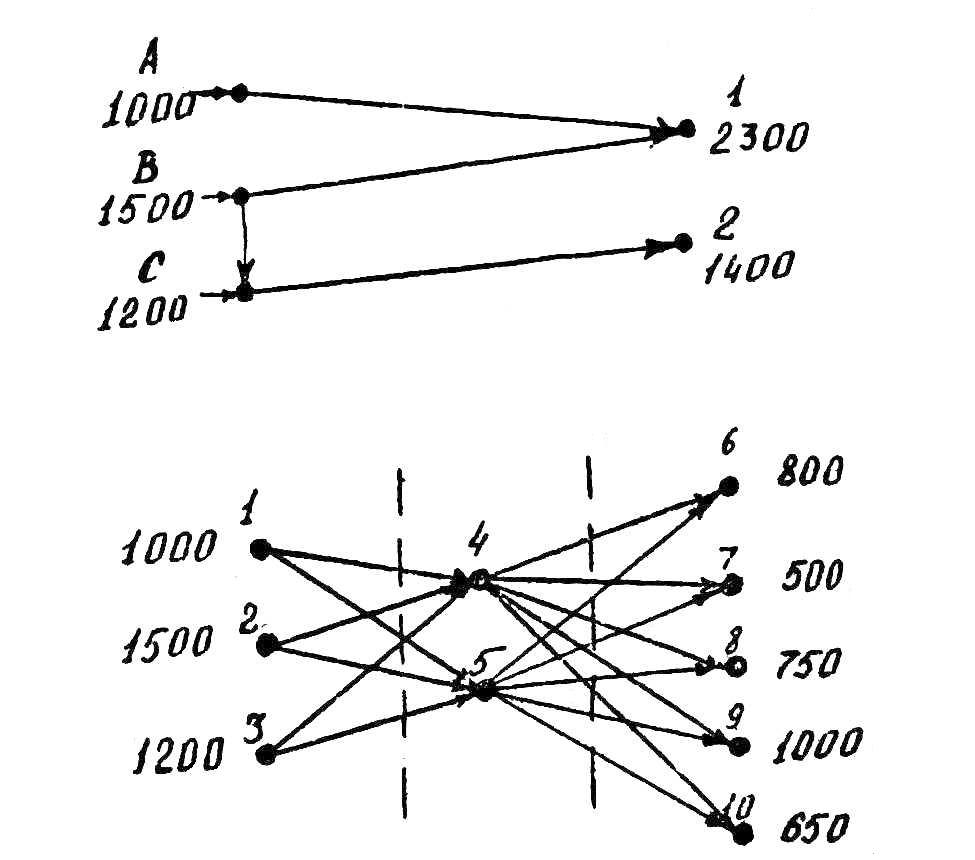

Рис. 3.3

Таблица 3.14

	4	5	6	7	8	9	10
1								1000
2								1500
3								1200
4								3700
5								3700
	3700	3700	800	500	750	1000	650

Нужно отметить, что транспортная задача и ее варианты составляют единый класс обобщенных сетевых задач, что чрезвычайно важно для хозяйства связи.

Так, задачу о кратчайшем пути на сети связи можно сформулировать как транспортную задачу с промежуточными пунктами. Сеть, на которой отыскивается кратчайший путь, можно считать транспорт­ной сетью с одним исходным пунктом и одним пунктом назначения. Величина предложения в исходном пункте и величина спроса в пункте назначения равна I. Единица груза (единица информации) передается из исходного пункта в пункт назначения по допустимым маршрутам сети. Задача состоит в минимизации пути, проделанном единицей инфор­мации.

Для иллюстрации модели рассмотрим сеть, приведенную на рис. 3.4. В отличие от алгоритма для сетей без циклов, при котором автоматически вычисляются кратчайшие пути между узлом 1 всеми другими узлами, в модели с промежуточными пунктами находится крат­чайшее расстояние лишь между двумя пунктами. В табл. 3.15 представлена модель с промежуточными пунктами, соот­ветствующая задаче, в которой требуется определить кратчайшее расстояние между узлами 1 и 7. В этом случае емкость буфера равна 1, поскольку в любой момент через любой узел сети проходит не более одной единицы груза. Заметим также, что узел 1 не мо­жет рассматриваться в качестве промежуточного пункта назначения, поскольку он является исходным пунктом для всей сети. Аналогич­но узел 7 не может быть промежуточным пунктом, поскольку он яв­ляется конечным пунктом доставки информации. "Стоимости перевоз­ки" полагаются равными соответствующим расстояниям на сети. Заштрихованные ячейки таблицы означают, что такого маршрута не су­ществует и, следовательно, при решении задачи им следует пробе­жать очень большое расстояние. Расстояние от некоторого узла до него самого полагается равным нулю.

Рис. 3.4

Таблица 3.14

	2	3	4	5	6	7
1	1 2	8	5	9			1
2	0	3		5	1 1		0+D
3	4	1 0			2		0+D
4		9	1 0		2	23	0+D
5				0	7	1 9	0+D
6	8	3	5	1 1	0	10	0+D
	0+D	0+D	0+D	0+D	0+D	1

Задача решается как типичная транспортная задача. Из таблицы следует, что

x₁₂=1, x₂₆=1, x₃₃=1, x₄₄=1, x₅₇=1, x₆₅=1.

Величины x₃₃=x₄₄=1 не дают вклада в решение, поскольку они соответствуют петлям в узлах 3 и 4. Остальные величины мож­но упорядочить следующим образом:

x₁₂=1, x₂₆=1, x₆₅=1, x₅₇=1

Поэтому оптимальный маршрут выглядит так:

12657.