6 Выполнение блок-схемы
Наиболее наглядным способом описания алгоритма является блок-схема алгоритма, которая составляется на основании требований ГОСТ 19.701-90.
Блок-схема алгоритма представляет собой последовательность графических изображений (символов), соединенных линиями. Внутри символов словами или с помощью формул указывают выполняемую функцию (ввод исходных данных; вычисление расчетных параметров; условие, изменяющее направление выполнения алгоритма). В таблице 1 представлены основные символы для написания блок-схемы.
Таблица 1 – Основные символы для написания блок-схемы
Символ |
Назначение |
1 |
2 |
|
Начало или конец алгоритма или программы
|
|
Ввод – вывод данных |
|
Выполнение арифметических операций, вычисление расчетных параметров |
|
Использование ранее созданных и отдельно описанных алгоритмов, программ и подпрограмм |
|
Организация циклических процессов с заданным числом повторений |
|
Выбор направления выполнения алгоритма в зависимости от условия |
|
Организация циклических процессов с неизвестным числом повторений. (В программе используется для оператора повтора While) |
|
|
Окончание таблицы 1 |
|
1 |
2 |
|
Организация циклических процессов с неизвестным числом повторений. (В программе используется для оператора повтора Repeat) |
Потоки данных или потоки управления в схемах показываются прямыми линиями. Направление потока слева направо и сверху вниз считается стандартным. В случаях, когда нужно внести большую ясность в схему (например, при соединениях), на линиях используют стрелки. Если поток имеет направление отличное от стандартного, то стрелки должны указывать это направление.
7 Защита курсовой работы
Защита курсовой работы разрешается после проверки ее и соответствующего разрешения руководителя. Защита курсовой работы проводится перед комиссией с участием руководителя в установленные сроки. Для защиты студент готовит краткий доклад, в котором освещаются основные вопросы разработки. После доклада студент отвечает на вопросы, поставленные членами комиссии.
Оценка выставляется на основе анализа пояснительной записки, доклада, демонстрации программных средств и ответов на вопросы.
8 Пример выполнения заданий по курсовой работе
8.1
Пример
выполнения задачи 1. Необходимо
создать приложение для вычисления суммы
ряда с точностью
= 0,001,
общий член которого
.
Результаты вычислений вывести на форму.
Блок-схема задачи. Для решения поставленной задачи был разработан алгоритм, представленный в графическом виде (в виде блок-схемы) на рисунке 8.1. На рисунке 8.2 представлена блок-схема подпрограммы для вычисления факториала любого числа.
Рисунок 8.1 – Блок-схема решения задачи
Рисунок 8.2 – Блок-схема подпрограммы для вычисления факториала любого числа.
Форма приложения. Для решения задачи в Delhpi было разработано приложение. Вид окна приложения до выполнения вычислений представлен на рисунке 8.3. На рисунке 8.4 представлена форма приложения с результатами вычислений.
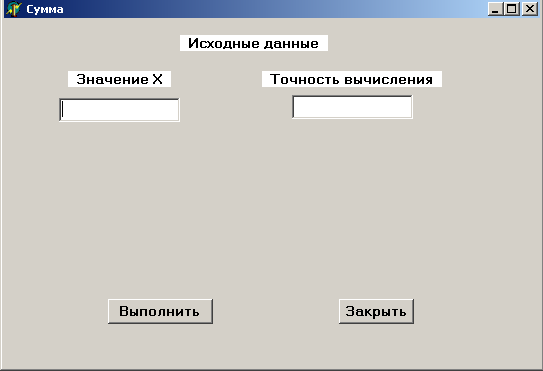
Рисунок 8.3 – Исходная форма приложения
Рисунок 8.4 – Форма приложения с результатами вычислений
На форме расположены следующие компоненты:
Label - компоненты для вывода текста (7 штук);
Edit – поля редактирования (5 штук);
Button – кнопки (2 штуки).
Текст программного модуля. Ниже приведен программный код разработанного приложения.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Label1: TLabel;
Edit1: TEdit;
Label2: TLabel;
Edit2: TEdit;
Button1: TButton;
Button2: TButton;
Label3: TLabel;
Edit3: TEdit;
Label4: TLabel;
Label5: TLabel;
Edit4: TEdit;
Label6: TLabel;
Label7: TLabel;
Edit5: TEdit;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
Function Fact(n:integer):integer;
var
i:integer;
F:integer;
begin
F:=1;
for i:=1 to n do
F:=F*i;
Fact:=F;
end;
procedure TForm1.Button1Click(Sender: TObject);
Var i,k : integer;
S,a,X,Eps : real;
begin
i:=1;
S:=0;
X:=StrToFloat(Edit1.Text);
Eps:=StrToFloat(Edit3.Text);
Repeat
If i Mod 2 = 0 then k:=1 else k:=-1;
a:=k*X*Fact(i)/Fact(2*i);
S:=s+a;
i:=i+1
until Abs(a)<=Eps;
Label2.Visible:=True;
Label4.Visible:=True;
Label5.Visible:=True;
Label7.Visible:=True;
Edit2.Visible:=True;
Edit4.Visible:=True;
Edit5.Visible:=True;
Edit2.Text:=FloatToStrF(s,ffFixed,10,4);
Edit4.Text:=FloatToStr(i-1);
Edit5.Text:=FloatToStrF(a,ffFixed,10,4);
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
Close;
end;
end.
Описание основных операторов, процедур, функций и методов. В процессе создания программного приложения использовались следующие функции:
- StrToFloat(s: string): extended; - преобразует строку в число, возвращаемый результат типа Extended;
- FloatToStrF(Value: Extended; Format: TFloatFormat; Precision, Digits: Integer): string; - преобразует число в строку, возвращаемый результат типа string.
В приложении использованы методы обработки событий, происходящих на форме, код которых создан во время работы приложения:
procedure Button1Click(Sender: TObject); - нажатие на кнопку Button1;
procedure Button2Click(Sender: TObject); - нажатие на кнопку Button2.
При написании кода использовались следующие операторы:
1) условный оператор:
If <логическое выражение> then <оператор1>
else <оператор2>;
Условный оператор работает следующим образом. Вычисляется значение логического выражения. Если оно истинно, то выполняется < оператор 1>, в противном случае выполняется <оператор2>;
2) оператор повтора:
Repeat
<оператор1>;
< оператор2>;
…
< операторN>
until <логическое выражение >;
Тело цикла выполняется пока значение логического выражения ложно.
Для вычисления значения факториала любого числа была написана пользовательская функция Function F(x:real):real.
8.2 Пример выполнения задачи 2. Необходимо создать приложение, которое должно обеспечить визуальное отображение перемещений объекта, представленного на рисунке 8.5.
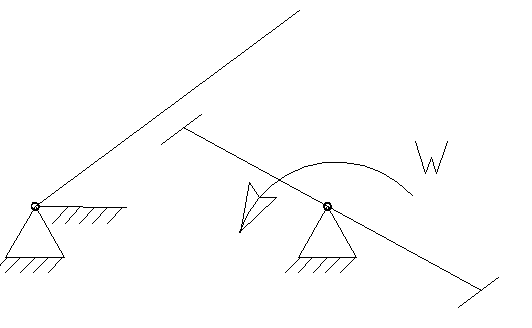
Рисунок 8.5 - Исходный механизм
Математическая модель. Для составления математической модели необходимо проанализировать работу механизма, выявить зависимости, однозначно определяющие положение механизма на плоскости.
На данном механизме заданы две опоры и два звена. В качестве переменной, определяющей положение, механизма задана переменная W. В таком случае положение механизма однозначно определяется переменной W. В зависимости от изменения положения вращающегося звена изменяется положение механизма в целом. Качающееся звено (кулиса) может изменять положение в первой четверти декартовой системы координат.
Зададим точки, определяющие положение механизма (рисунок 8.6).
Рисунок 8.6 - Точки, определяющие положение механизма
На основании схемы, приведенной на рисунке 8.6, составим математическую модель, описывающую положение механизма в зависимости от изменения угла W. В связи с изменением геометрических параметров механизма на плоскости, принимаем за текущую декартову систему координат с направлением осей Х и Y.
Координаты Хс, Yс, Хо, Уо задаются пользователем. Задается также расстояние СО. Принимается Yc равным Yo .Точка E совпадает с точкой В.
Длины звеньев BA = L1 и CD = L2 задаются пользователем. Причем BO = OA = L1/2 .
Тогда:
если α < 0, то принимаем α = 0; тогда
На основании созданной математической модели необходимо составить алгоритм программного приложения. Для простых приложений не требуются блок-схемы алгоритмов.
Составим алгоритм в вербальной форме. В связи с изменением геометрических характеристик системы в зависимости от переменной w, алгоритм предполагает наличие как минимум одного цикла. Таким образом:
- определяем начальное положение системы при значении w равным 0;
- производим рисование элементов системы на экране;
- определяем новое значение переменной w;
- определяем новое положение системы в зависимости от переменной w;
- стираем элементы системы, соответствующие старому значению w;
- Производим рисование элементов системы на экране, в соответствии с новым значением w;
- отдельно предусматриваем выход из программного приложения.
Описание основных операторов, процедур, функций и методов .В процессе создания программного приложения необходимо использование следующих функций:
- strToFloat(s: string): extended; - преобразует строку в число, возвращаемый результат типа Extended;
- strToInt(s: string): integer; - преобразует строку в число, возвращаемый результат типа integer;
- FloatToStr(F:extended):string; - преобразует число в строку, возвращаемый результата типа string;
-Round(x: real): integer; - преобразует вещественное число в целое;
- функции определения тригонометрических величин sin(х), cos(х).
Методы объекта canvas, обеспечивающие рисование на элементах формы:
- MoveTo(X,Y); - перемещает курсор в позицию, заданную координатами X и Y;
- LineTo(X,Y); - рисует отрезок из текущей точки в позицию, заданную координатами X и Y;
- Rectangle(X1,Y1,X2,Y2); - рисует прямоугольник с координатами левого верхнего угла X1, Y1 и правого нижнего угла с координатами X2, Y2.
Кроме описанных выше, в приложении использованы методы, обработки событий, происходящих на форме, код которых создан во время работы приложения:
- procedure FormCreate(Sender: TObject); - создание приложения;
- procedure Button1Click(Sender: TObject); - нажатие на кнопку1;
- procedure FormResize(Sender: TObject); - изменение размера формы;
- procedure SpinEdit1Change(Sender: TObject) - изменение содержимого SpinEdit;
- procedure Edit2Change(Sender: TObject) - изменение содержимого Edit2.
Форма приложения. Одним из основных элементов приложения является форма, из которой пользователь управляет событиями, происходящими во время работы приложения. Форма приложения представлена на рисунке 8.7
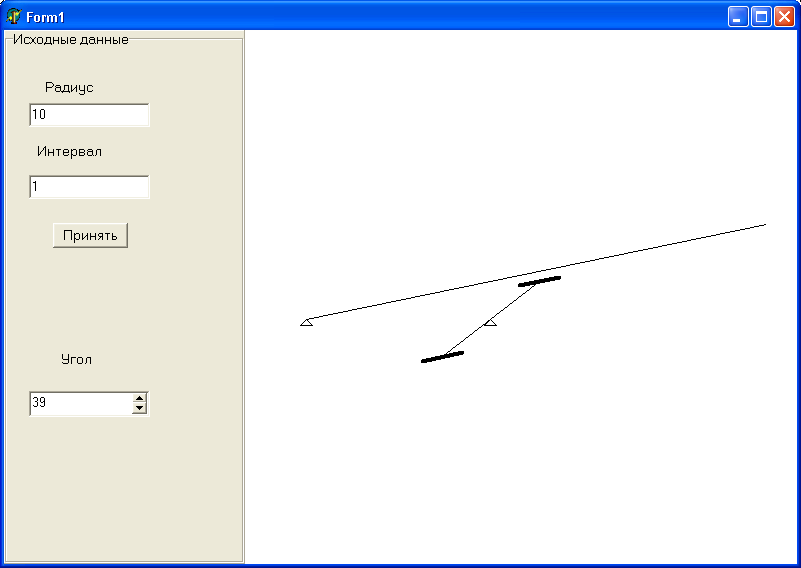
Рисунок 8.7 – Форма приложения
На форме размещены следующие компоненты:
Label1, Label2, Label3 – компоненты для вывода текста, содержащие статичный текст и несущие информацию о назначении других компонентов;
Edit1, Edit2 - поля редактирования, содержащие значения вводимых величин;
SpiEdit1 - строка, содержащая числовое значение переменной w;
Button1 - кнопка для принятия новых данных;
Image1 – место для рисования схемы.
Текст программы. Ниже приведен текст программного кода для решения поставленной задачи. Комментарии размещены в тексте приложения в соответствии с синтаксисом Delphi.
unit Kulisa;
interface
uses Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls, ExtCtrls, Spin;
Type
KL = Сlass // описание пользовательского класса
r, // радиус
Xn, // начало левой опоры по Х
Yn, // по У
Xo, // центр поворота по Х
Yo, // по У
Xa, // координата точки А по Х
Ya, // по У
Xb, // координата точки В по Х
Yb, // по У
rm, // длина малого отрезка
l, // длина большого отрезка
alf, // угол наклона кулисы
lx,ly, //координаты по Х и У
K, Kx,Ky, // максимальная длина большого отрезка
Xmax, Ymax, // максимальная длина по Х и У
w,wOld // Угол поворота
: real;
Im : TImage;
Mx,My : real; // масштабные коэффициенты
Constructor Create; // инициализация значения Im
Procedure GetData; // задание исходных данных
Procedure GetW(al:integer); // задание переменной W
Procedure CalcData(al:real); // расчет значений исходных данных
Procedure Draw; // рисование объекта
Procedure Hide; // стирание объекта
Procedure Ris; // рисование и стирание
Procedure CalcMXY; // рассчет масштабных коэффициентов
Function OutX(X : real) : integer; // преобразование значения Х
Function OutY(Y : real) : integer; // преобразование значения У
end;
type
TForm1 = class(TForm) // описание формы и ее событий
Panel1: TPanel;
GroupBox1: TGroupBox;
Label1: TLabel;
Edit1: TEdit;
Panel2: TPanel;
Image1: TImage;
Button1: TButton;
SpinEdit1: TSpinEdit;
Edit2: TEdit;
Label2: TLabel;
Label3: TLabel;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure FormResize(Sender: TObject);
procedure SpinEdit1Change(Sender: TObject);
procedure Edit2Change(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
kL1 : KL; // объявление объекта
implementation
{$R *.DFM}
Constructor Kl.Create;
begin
Im := Form1.Image1; // присвоение переменной Im значения Image1 из формы
end;
// задание начальных значений положения механизма
Procedure Kl.GetData;
begin
r := StrToFloat(Form1.Edit1.Text);
Xn := 10;
Yn := 4*r;
Xo := Xn + 3*r;
Yo := Yn;
W := 0;
end;
{Получение нового угла}
Procedure Kl.GetW(al:integer);
begin
wOld := W;
W := Al*Pi/180;
end;
{Расчет параметров в соответствии с математической моделью}
Procedure Kl.CalcData(al:real);
begin
Xa := Xo + r*cos(Al);
Ya := Yo + r*sin(Al);
Xb := Xo - r*cos(Al);
Yb := Yo - r*sin(Al);
if cos(Al) >= 0 then
begin
lx := Xa;
ly := Ya;
end
else begin
lx := Xb;
ly := Yb;
end;
l := Sqrt(Sqr(lx)+Sqr(ly));
alf := arctan(r*sin(Al)/(Xo-Xn));
if Alf < 0 then Alf := Abs(Alf);
Xmax := Xo + 5*r;
Ymax := 2*r;
K := l + r;
Kx := Xn + K*cos(Alf);
Ky := Yn + k*sin(Alf);
rm := r/3;
end;
{Расчет масштабных коэффициентов}
Procedure Kl.CalcMXY;
begin
Mx := Im.Width / Xmax;
My := Im.Height / Ymax;
if Mx < My Then My := Mx
else Mx := My;
end;
{Рассчет значения Х}
Function Kl.OutX;
begin
OutX := Round(X*Mx);
end;
{Расчет значения У}
Function Kl.OutY;
begin
OutY := Im.Height - Round(Y*My);
end;
{Рисование }
Procedure Kl.Draw;
begin
CalcData(wOld);
Hide;
Im.Canvas.Pen.Width := 1;
Im.Canvas.Pen.Color := clBlack;
Ris;
end;
{Стирание}
Procedure Kl.Hide;
begin
Im.Picture := Nil
end;
{Отрисовка}
Procedure Kl.Ris;
begin
With Im.Canvas do
begin
{Рисование опоры под С}
MoveTo(OutX(Xn),OutY(Yn));
LineTo(OutX(Xn-r/10),OutY(Yn-r/10));
LineTo(OutX(Xn+r/10),OutY(Yn-r/10));
LineTo(OutX(Xn),OutY(Yn));
{Рисование опоры под О}
MoveTo(OutX(Xo),OutY(Yo));
LineTo(OutX(Xo-r/10),OutY(Yo-r/10));
LineTo(OutX(Xo+r/10),OutY(Yo-r/10));
LineTo(OutX(Xo),OutY(Yo));
{Рисование вращающегося отрезка}
MoveTo(OutX(Xb),OutY(Yb));
LineTo(OutX(Xa),OutY(Ya));
{Рисование большого отрезка}
MoveTo(OutX(Xn),OutY(Yn));
LineTo(OutX(Kx),OutY(Ky));
{Рисование маленьких отрезков}
Pen.Width := 4;
{В точке А}
MoveTo(OutX(Xa-rm*Cos(Alf)),OutY(Ya-rm*sin(Alf)));
LineTo(OutX(Xa+rm*Cos(Alf)),OutY(Ya+rm*sin(Alf)));
{В точке В}
MoveTo(OutX(Xb-rm*Cos(Alf)),OutY(Yb-rm*sin(Alf)));
LineTo(OutX(Xb+rm*Cos(Alf)),OutY(Yb+rm*sin(Alf)));
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Kl1.Create;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Kl1.GetData;
Kl1.CalcData(Kl1.w);
Kl1.CalcMXY;
Kl1.Draw;
end;
procedure TForm1.FormResize(Sender: TObject);
begin
Kl1.Im.Picture := Nil;
Kl1.Im.Canvas.Pen.Color := clWhite;
Kl1.Im.Canvas.Rectangle(0,0,Kl1.Im.Width,Kl1.Im.Height);
end;
procedure TForm1.SpinEdit1Change(Sender: TObject);
begin
if SpinEdit1.Value > 360 then SpinEdit1.Value := 1;
Kl1.GetW(SpinEdit1.Value);
Kl1.CalcData(Kl1.W);
Kl1.Draw;
end;
procedure TForm1.Edit2Change(Sender: TObject);
begin
SpinEdit1.Increment := StrToInt(Edit2.Text);
end;
end.