Задание №8. Рызбаев р.
Задача 1
К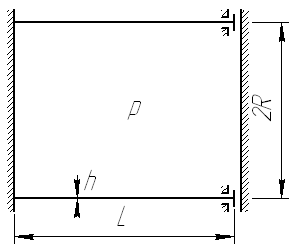
ороткая
цилиндрическая оболочка радиуса R,
длины L
и толщины h
нагружена внутренним давлением р.
По левому торцу оболочка защемлена, по
правому – «скользящая заделка». Найдите
аналитически перемещения и внутренние
силовые факторы в оболочке. Числовые
значения возьмите из таблицы.
|
R[м] |
L[м] |
h[мм] |
p[МПа] |
E[МПа] |
µ |
1 |
1.00 |
0.50 |
1.75 |
0.01 |
|
|
Нужно найти общее решение дифференциального уравнения
Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.
Общее решение однородного уравнения.
Характеристическое уравнение , где
Корни характеристического уравнения : ; ; ; .
Решение, соответствующее найденным корням
Общее решение неоднородного уравнения
Это решение нужно подчинить граничным условиям. При : и ; при : и
Задача 2
Выполнить расчет цилиндрической оболочки нагретой до температуры , градиент температуры по толщине и нагруженной внутренним давлением . Параметры оболочки и характеристики материала взять из таблицы. При расчете оболочки использовать теорию краевого эффекта. Построить графики поперечного перемещения , изгибающего момента , эквивалентного напряжения в зоне краевого эффекта с частичным охватом безмоментной зоны. Сравните полученные эквивалентные напряжения с приведенными в таблице характеристик и сделайте заключение о прочности оболочки. Расчетные формулы для второй задачи приведены в отдельном текстовом файле.
|
R[м] |
L[м] |
h[мм] |
E[МПа] |
[ ] |
µ |
1 |
0.025 |
0.70 |
4.00 |
|
|
|
|
[ ] |
[ ] |
[МПа] |
[МПа] |
[МПа] |
[МПа] |
|
600 |
0 |
0,00 |
0,03 |
400 |
180 |
|
Граничные условия на левом конце |
шарнир |
|
|
|
|
Задание №9. Сафронова т.
Задача 1
К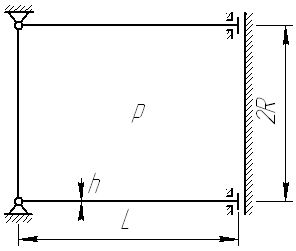
ороткая
цилиндрическая оболочка радиуса R,
длины L
и толщины h
нагружена внутренним давлением р.
По левому торцу оболочка закреплена
шарнирно, по правому – «скользящая
заделка». Найдите аналитически перемещения
и внутренние силовые факторы в оболочке.
Исходные данные возьмите из таблицы.
|
R[м] |
L[м] |
h[мм] |
p[МПа] |
E[МПа] |
µ |
1 |
1.00 |
0.50 |
2.00 |
0.01 |
|
|
Нужно найти общее решение дифференциального уравнения
Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.
Общее решение однородного уравнения. Характеристическое уравнение , где
Корни характеристического уравнения: ; ; ; .
Решение, соответствующее найденным корням
Общее решение неоднородного уравнения
Это решение нужно
подчинить граничным условиям. При
:
;
;
при
;
Задача 2
Выполнить расчет цилиндрической оболочки нагретой до температуры , градиент температуры по толщине и нагруженной внутренним давлением . Параметры оболочки и характеристики материала взять из таблицы. При расчете оболочки использовать теорию краевого эффекта. Построить графики поперечного перемещения , изгибающего момента , эквивалентного напряжения в зоне краевого эффекта с частичным охватом безмоментной зоны. Сравните полученные эквивалентные напряжения с приведенными в таблице характеристик и сделайте заключение о прочности оболочки. Расчетные формулы для второй задачи приведены в отдельном текстовом файле.
|
R[м] |
L[м] |
h[мм] |
E[МПа] |
[ ] |
µ |
1 |
0.025 |
0.70 |
5.00 |
|
|
|
|
[ ] |
[ |
[МПа] |
[МПа] |
[МПа] |
[МПа] |
|
600 |
0 |
0,0 |
0,03 |
400 |
180 |
|
Граничные условия на левом конце |
шарнир |
|
|
|
|
]