Министерство образования и науки Российской Федерации

Московский ордена Ленина, ордена Октябрьской Революции и ордена Трудового Красного Знамени государственный технический университет имени н. Э. Баумана

Факультет Аэрокосмический

Кафедра см 2

З А Д А Н И Е

на курсовую работу по курсу: «Прочность КР»

Студент: ________________АК2-101

Руководитель: ________________.;

Срок выполнения работы по графику: 50% к 7 нед., 100% к 13 нед.

Защита курсовой работы на комиссии 14 неделя.

Модули и рейтинги

1.Модуль 1. Решение первой задачи. 7 неделя, 30 баллов

2.Модуль 2. Решение второй задачи. 13 неделя, 30 баллов

Защита курсовой работы 60 баллов.

Защита работы 2013 г.

I Тема работы: “Расчет оболочек”.

II Содержание задания:

1.Решение задачи о напряженно-деформированном состоянии тонкостенной конструкции по безмоментной теории с применением теории краевого эффекта

Индивидуальное задание с методическими рекомендациями по выполнению для каждого студента

2.Расчет цилиндрической оболочки при действии нагрева и внутреннего давления

Индивидуальное задание для каждого студента с общими для всех методическими указаниями.

Руководитель работы:

Дата выдачи “15“ февраля 2013г.

Перечень вопросов на защите

1.Уравнения закона Гука для плоского напряженного состояния

2.Учет нагрева. Соотношения Дюамеля-Неймана

3.Физические уравнения моментной теории цилиндрической оболочки при осесимметричной деформации

4.Уравнения равновесия цилиндрической оболочки при осесимметричной деформации

5.Безмоментная теория оболочек. Основные допущения. Методы расчета.

6.Когда может быть использована безмоментная теори

6.Теория краевого эффекта

7.Оценка размеров зоны краевого эффекта.

8.Когда может быть применена теория краевого эффекта.

Задание №1. Зверев н.

Задача 1

Полубесконечная цилиндрическая оболочка, шарнирно опертая по левому торцу, нагружена внутренним давлением р, толщина оболочки h, радиус срединной поверхности R. Используя теорию краевого эффекта, постройте эпюры перемещений и изгибающих моментов вблизи левого торца. Исходные данные возьмите из таблицы.

	R[м]	h[мм]	p[МПа]	E[МПа]	µ
1	1.00	1.75	0.01

Нужно найти общее решение дифференциального уравнения

Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.

Общее решение однородного уравнения.

Характеристическое уравнение , где

Корни характеристического уравнения : ; ; ; .

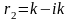Решение, соответствующее найденным корням

Общее решение неоднородного уравнения

Это решение нужно подчинить граничным условиям. На бесконечности условие ограниченности решения. При : ;

Задача 2

Выполнить расчет цилиндрической оболочки нагретой до температуры , градиент температуры по толщине и нагруженной внутренним давлением . Параметры оболочки и характеристики материала взять из таблицы. При расчете оболочки использовать теорию краевого эффекта. Построить графики поперечного перемещения , изгибающего момента , эквивалентного напряжения в зоне краевого эффекта с частичным охватом безмоментной зоны. Сравните полученные эквивалентные напряжения с приведенными в таблице характеристик и сделайте заключение о прочности оболочки. Расчетные формулы для второй задачи приведены в отдельном текстовом файле.

	R[м]	L[м]	h[мм]	E[МПа]	[ ]	µ
1	0.025	0.70	5.00
	[ ]	[ ]	[МПа]	[МПа]	[МПа]	[МПа]
	600	10	0,00	0,03	400	180
	Граничные условия на левом конце	заделка