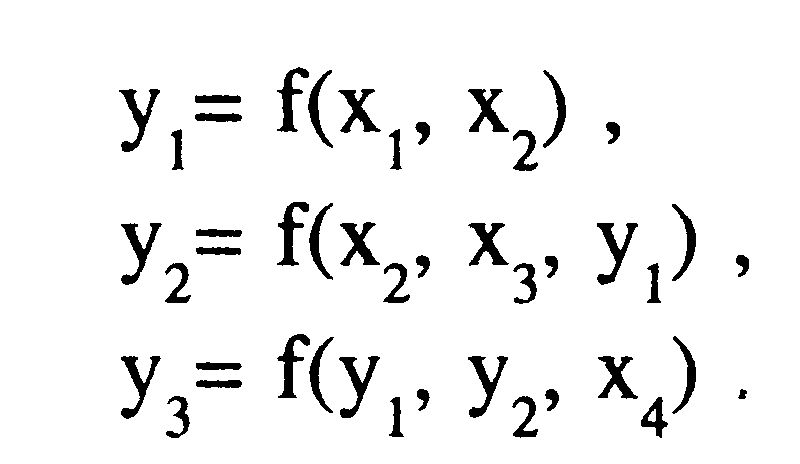Метод экспоненциального сглаживания

Часто используемый для прогноза в на ближайший период, он преодолевает один значительный недостаток метода плавающего среднего. Метод экспоненциального сглаживания модифицирует метод плавающего среднего, систематически выделяя данные за последние периоды и ставит меньший акцент на более старые данные.

Наиболее распространенная формула метода экспоненциального сглаживания:

F_(t+1)=*S_t+(1-)* F_t

Где  - постоянная сглаживания

F_t – прогноз продаж на текущий период

S_t - действительные продажи за текущий период

Самое критическое решение – величина . Маленькое  используется, если продажи стабильны. Высокое  – придает больший вес данным за последний период.

Пример расчета прогноза продаж методом экспоненциального сглаживания.

Месяц	Исторические данные	Прогноз продаж
		=0,2
Январь	1,002
Февраль	1,38	1,002*
Март	1,19	1,078
Апрель	2,016	1,100
Май	1,842	1,283
Июнь	1,543	1,395
Июль	1,328	1,425=0,2*1,543+0,8*1,395
Август	1,276	1,406
Сентябрь	1,762	1,380
Октябрь	1,981	1,456
Ноябрь	1,49	1,561
Декабрь	1,206	1,547

* На первый период нет возможности использовать метод, поэтому просто ставится значение актуальных продаж за предыдущий период.

Задание рассчитайте прогноз продаж на каждый месяц при =0,4; =0,8. Сравните результаты прогнозов с тремя разными значениями . При каком значении  прогноз продаж получился точнее? Почему?

Корреляционно-регрессионный анализ

Пример определения коэффициентов корреляционной зависимости первого порядка для прогнозирования продаж

X, год	Y, продажи, $	XY	X2	Y=a+bX b=(4*650-10*239)/(4*30-100)=10.5 a=59.75-10.5*2.5=33.5 Y=33.5+10.5X
1	43	43	1
2	52	104	4
3	73	219	9
4	71	284	16
Всего 10	239	650	30
Среднее 2,5	59,75

Экспликативные (« объясняющие ») модели Модели с системой уравнений

Если изучаемое явление слишком сложно для описания его единст­венным уравнением, аналитик должен выбрать такой метод оценки, ко­торый позволяет учитывать взаимозависимость переменных.

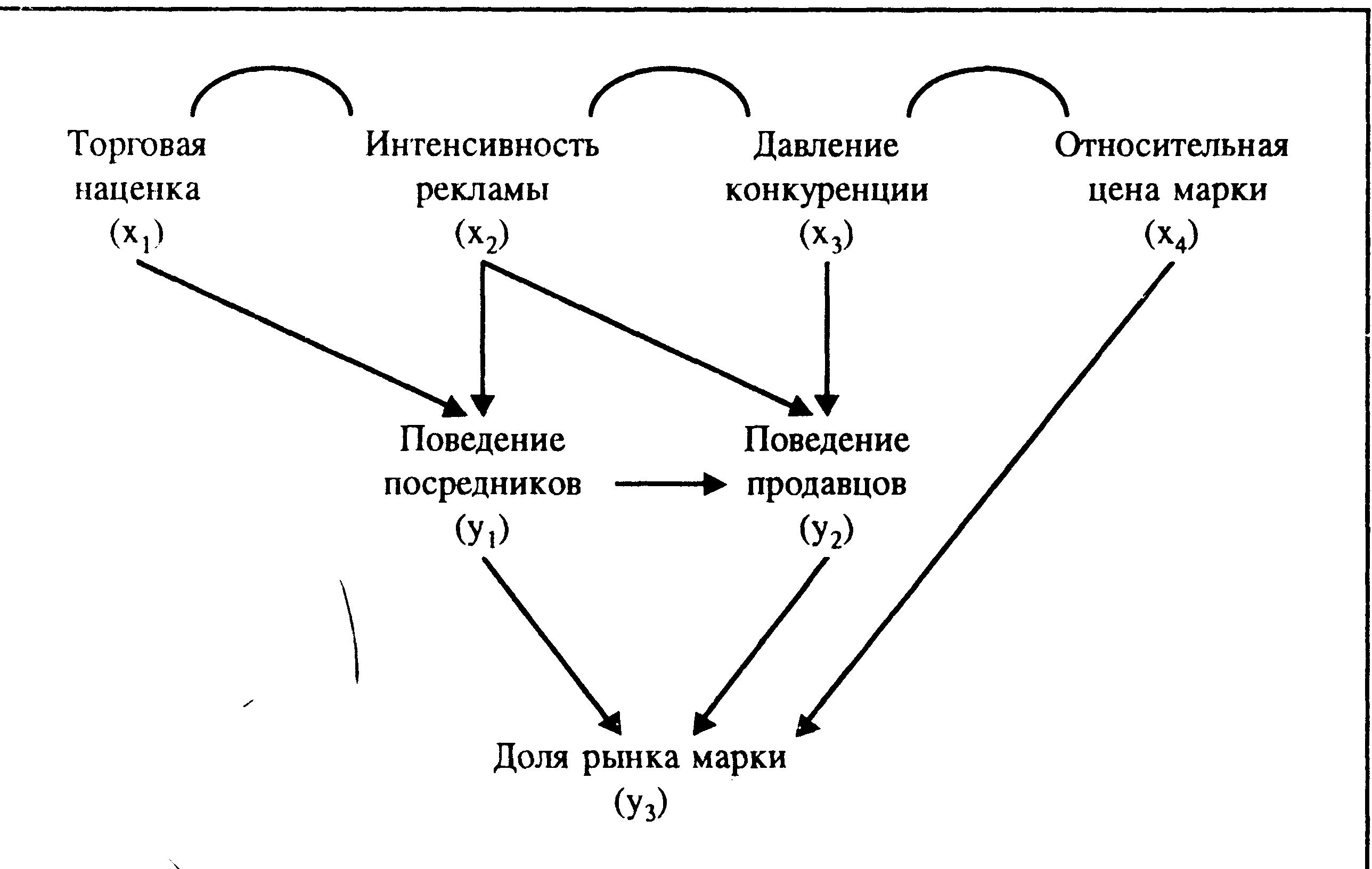
В качестве примера рассмотрим проблему измерения влияния рек­ламы на долю рынка для марки потребительского товара, продаваемого через широкую сбытовую сеть. Предыдущие исследования эффективно­сти рекламы показали, что она непосредственно влияет на уровень узна­вания марки и на поведение продавцов, ответственных за сбыт марки в сети. Таким образом, причинная структура явления может быть представлена

Пример причинной структуры. Влияние рекламы на долю рынка. поведение дистрибьютора (y1) определяется торговой наценкой, которую он получает (x1), и интенсивностью рекламных усилий в отношении марки (х2); поведение продавцов (у2) определяется поведением дистрибьюто­ров (y1), интенсивностью рекламы (х2) и давлением конкуренции(х3); уровень доли рынка (у3) определяется поведением дистрибьюто­ров (y1), поведением продавцов (у2) и относительным уровнем цены марки (х4).