3.1. Краткое содержание

Теплоемкость тела или термодинамической системы численно равна количеству теплоты, которое необходимо для нагревания его на один градус. Если в результате передачи телу количества теплоты температура выросла на , то

Теплоемкость тела зависит от его массы. Характеристикой для каждого тела будут удельная и молярная теплоемкости

,

Это теплоемкости, отнесенные к единице массы и одному молю вещества

,

В зависимости от условий нагревания теплоемкости одного и того же тела могут быть разными. Так, теплоемкость тела при постоянном давлении будет отличаться от его теплоемкости при постоянном объеме, т. е.

,

Молярная теплоемкость идеального газа при постоянном объеме , а при постоянном давлении

- число степеней свободы молекулы.

3. 2. Вопросы и задачи

1. Разность удельных теплоемкостей некоторого двухатомного газа равна 260 Дж/кг·К. Найти молярную массу газа и его удельные теплоемкости и .

2. Каковы удельные теплоемкости и смеси газов, содержащей кислород массой г и азот массой г?

3. Определить удельную теплоемкость смеси газов, содержащей л водорода и л гелия. Газы находятся при одинаковых условиях.

4. Определить удельную теплоемкость смеси кислорода и азота, если количество вещества первого компонента равно 2 моль, а количество вещества второго равно 4 моль.

5. Дан закон изменения молярной теплоемкости идеального газа в некотором процессе , где . Найти уравнение этого процесса в координатах .

6. Дан закон изменения молярной теплоемкости идеального газа в некотором процессе , где . Найти уравнение этого процесса.

7. Степень диссоциации газообразного водорода равна 0,6. Найти удельную теплоемкость такого частично диссоциировавшего водорода.

8. Тело с не зависящей от температуры теплоемкостью  Дж/К охлаждается от до . Определить количество теплоты , полученное телом.

9. В рассматриваемом интервале температур теплоемкость некоторого тела определяется функцией Дж/К. Определить количество теплоты , получаемое телом при нагревании от К до К.

10. Определить удельную теплоемкость смеси 50% по весу водорода и гелия, заключенной в объеме л при температуре и давлении  мм.рт.ст.. Молярные теплоемкости водорода  кал/(моль·°C) и гелия  кал/(моль·°C).

11. Для определения удельной теплоемкости цинка кусок его массы г нагрет до температуры и опущен в латунный калориметр. Удельная теплоемкость латуни  кал/(г·°C), масса калориметра и мешалки г, масса воды г, начальная температура калориметра и воды . Температура воды в калориметре повысилась до . Определить удельную теплоемкость цинка.

Занятие 4

Тема: Изопроцессы идеального газа

4.1. Краткое содержание.

1. Изотермический процесс.

Процесс, происходящий при постоянной температуре ( ).

Уравнение процесса , или

Подводимое к системе тепло идет на совершение работы, т. е.

Работа при изотермическом процессе

2. Изобарический процесс.

Уравнение процесса , или

Теплоемкость при изобарическом процессе

При , - энтальпия системы

Молярная теплоемкость при изобарическом процессе

3. Изохорический процесс.

Уравнение процесса , или

Молярная теплоемкость

4. Адиабатический процесс.

Это процесс, происходящий в термодинамической системе при условии ее полной термоизоляции

Уравнение процесса (уравнение Пуассона)

, где

Работа, выполняемая в адиабатическом процессе системой против внешних сил, совершается за счет уменьшения ее внутренней энергии.

, т.к.

5. Политропический процесс.

Реальные процессы являются промежуточными между изотермическим и адиабатическим процессами. Они называются политропическими и протекают при постоянной теплоемкости.

Уравнение политропического процесса

, где

4.2. Вопросы и задачи

1. Изменение состояния идеального газа происходит по уравнению . Удельная теплоемкость – задана.

1) Найти выражение для удельной теплоемкости через показатель и коэффициент Пуассона .

2) Рассмотреть частные случаи.

2. Один моль идеального газа переходит из состояния 1 с параметрами в состояние 2 с параметрами . Процесс перехода в координатах выражается прямой линией. График процесса представлен на рис. 4.1. прямой линией. Молярная теплоемкость в процессе перехода не зависит от температуры. Найти:

а) аналитическое выражение процесса перехода;

б) общую формулу для определения молярной теплоемкости для любого процесса;

в) молярную теплоемкость для данного процесса;

г) условия перехода данного процесса в политропический процесс;

д) молярную теплоемкость для полученного политропического процесса.

3. Изобразить для идеального газа примерные графики изохорического, изобарического, изотермического и адиабатического процессов на диаграммах: а) ; б) ; в) . Графики изобразить через общую для них точку.

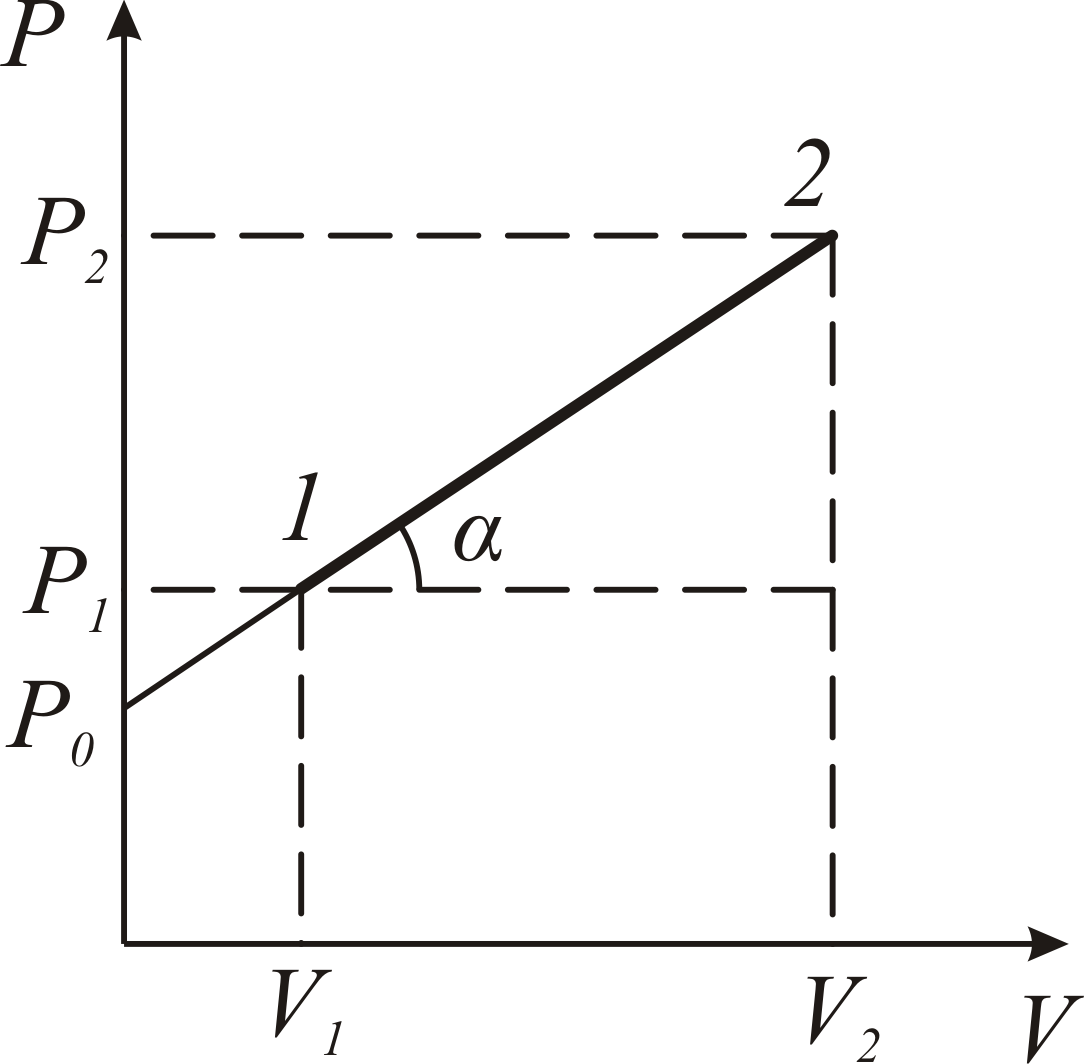
Рис. 4.1

4. Изобразить для идеального газа примерные графики:

а) изохорического, изобарического и адиабатического процессов на диаграмме ;

б) изохорического, изобарического, изотермического и адиабатического процессов на диаграммах и ; откладывать по оси ординат. Исходной для всех графиков принять общую точку.

5. Некоторое количество идеального газа с трехатомными жесткими молекулами перешло адиабатически из состояния с температурой  К в состояние, характеризуемое параметрами: К, Па, л. Какую работу совершает при этом газ?

6. Некоторое количество одноатомного идеального газа сжимают адиабатически до тех пор, пока давление не превзойдет начальное давление в 10 раз. Затем газ расширяется изотермически до первоначального объема. Во сколько раз конечное давление газа превышает начальное давление ?

7. Температура в комнате объема поднялась от значения до температуры . Как изменилась при этом внутренняя энергия воздуха, содержащегося в комнате? Атмосферное давление предполагается не изменившимся.

8. Атмосферное давление изменилось от гПа до гПа. Какое приращение получает при этом внутренняя энергия воздуха, содержащегося в комнате объема м³? Температура в комнате предполагается неизменной.

9. При изобарическом нагревании от 0 до моль идеального газа поглощает количество теплоты к Дж. Определить:

а) значение ;

б) приращение внутренней энергии газа ;

в) работу, совершаемую газом.

10. Выразить молярную теплоемкость идеального газа при политропическом процессе через показатель политропы и отношение теплоемкостей .

11. В ходе некоторого политропического процесса идеальный газ ( ) был сжат от объема л до объема л. При этом давление возросло от гПа до гПа. Определить:

а) показатель политропы ;

б) молярную теплоемкость газа для рассматриваемого процесса.

12. Моль одноатомного идеального газа нагревается обратимо от К до К. В процессе нагревания давление газа изменяется с температурой по закону , где К^-1. Определить количество теплоты, полученное газом при нагревании.

13. Состояние идеального газа изменяется по политропе . Найти работу, совершаемую молем газа при повышении его температуры от до .

Занятие 5

Тема: Энтропия идеального газа