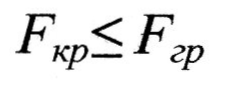- •Математичне моделювання, математичне планування і оптимізація багатофакторних експериментів та їх застосування у сучасних економічних дослідженнях.
- •Приклади отримання поверхонь відгуку, що геометрично відображають шукані аналітичні значення.
- •Розрахунок коефіцієнтів регресії багатофакторного поліномінального лінійного рівняння з допомогою методу найменших квадратів.
- •1. Однофакторне рівняння регресії.
- •2.Розглянемо загальний випадок: параметр уі; є функцією не тільки багатьох змінних, але і їх добутків - членів міжфакторної взаємодії.
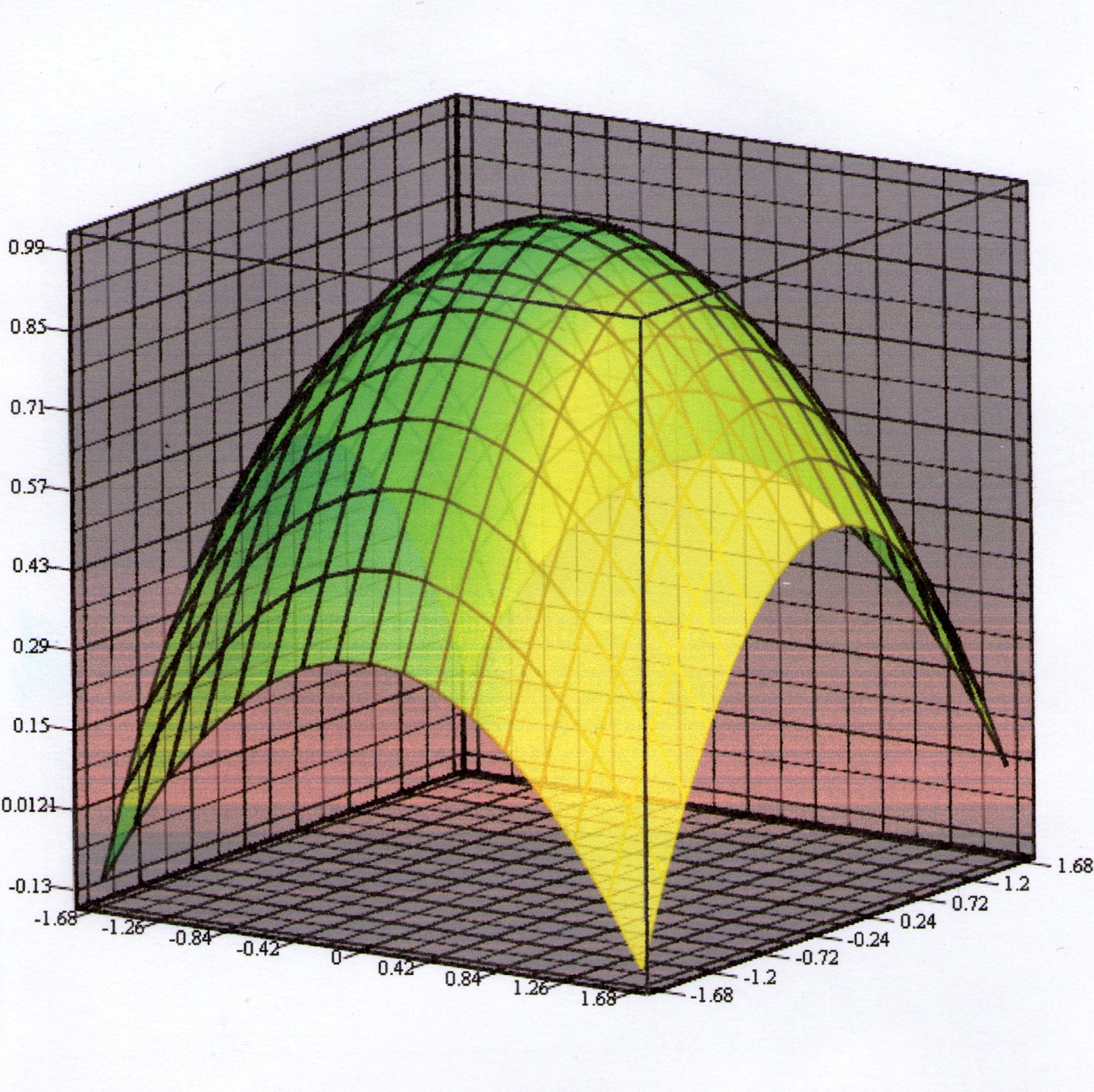
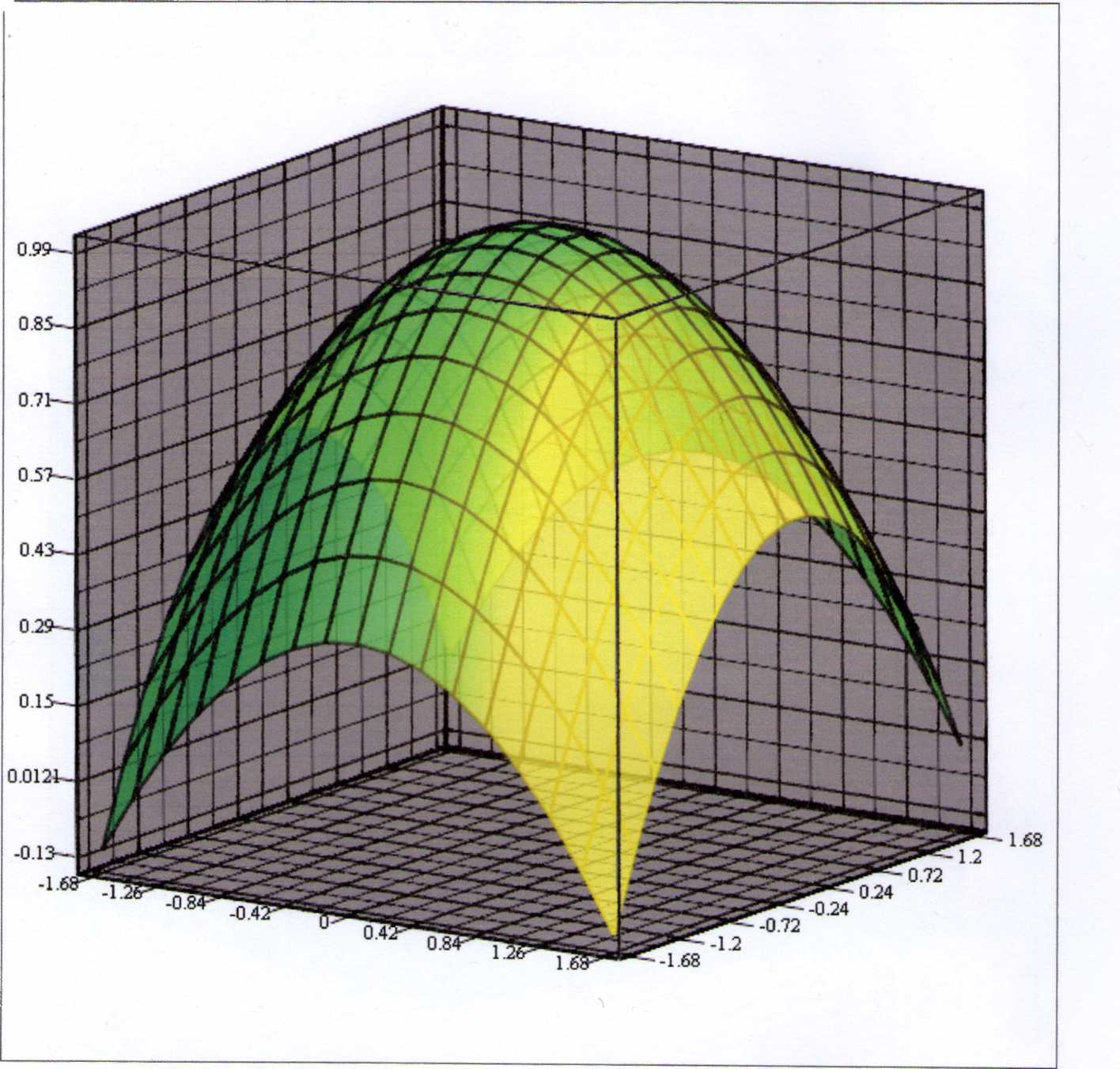
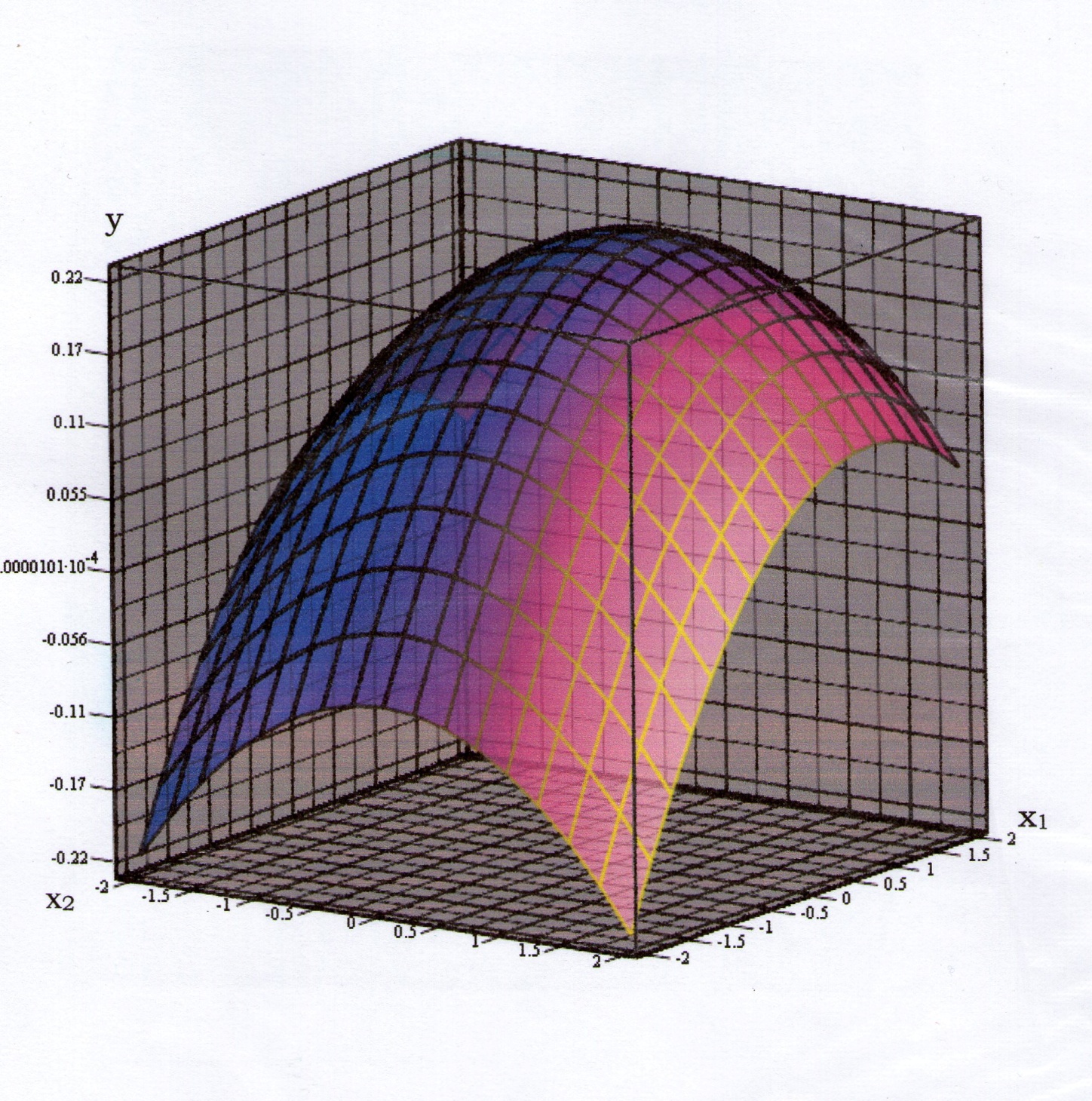
- •1. Просторова двохвимірна область планування для кодованих значень незалежних змінних у двохфакторному дослідженні.
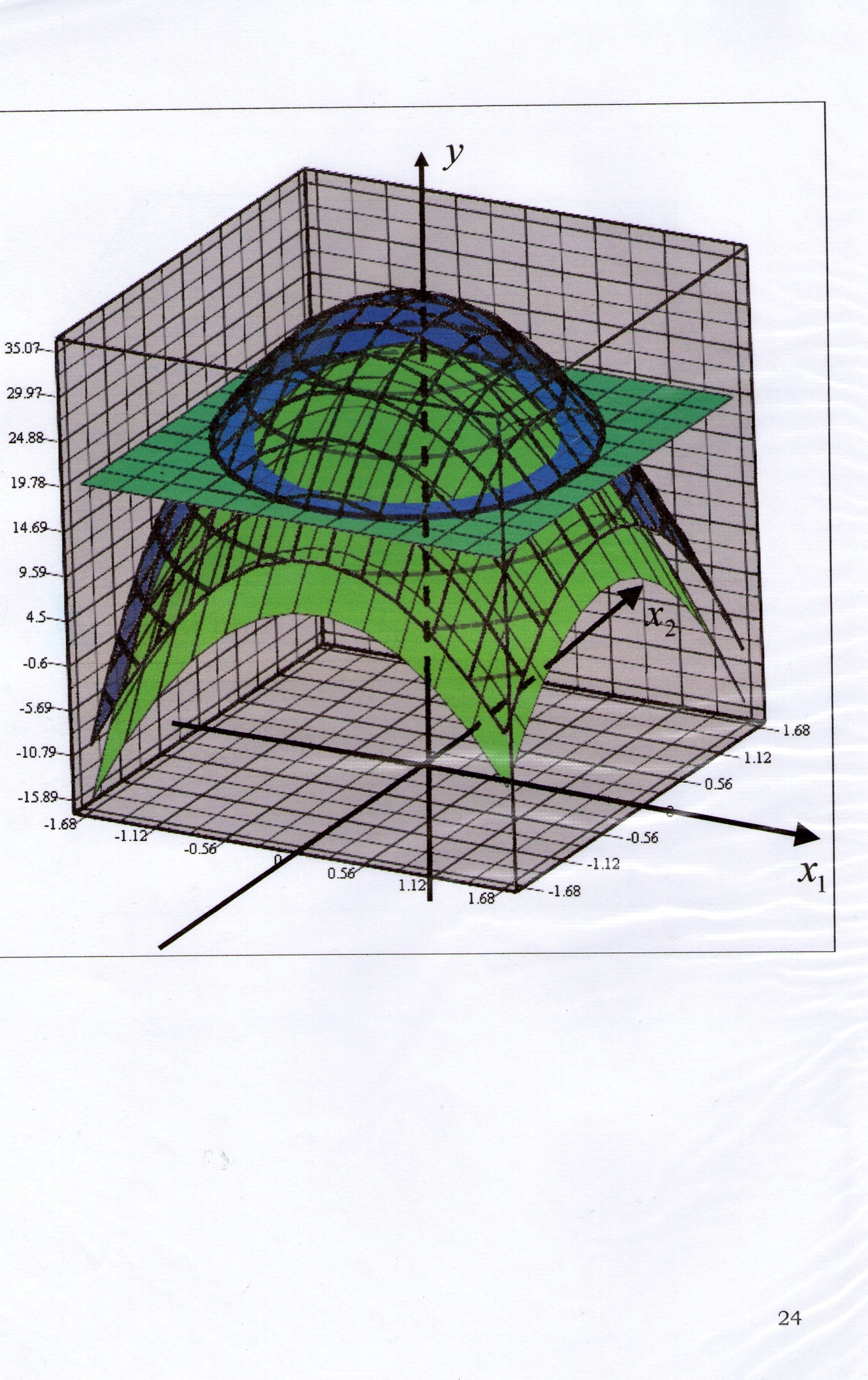
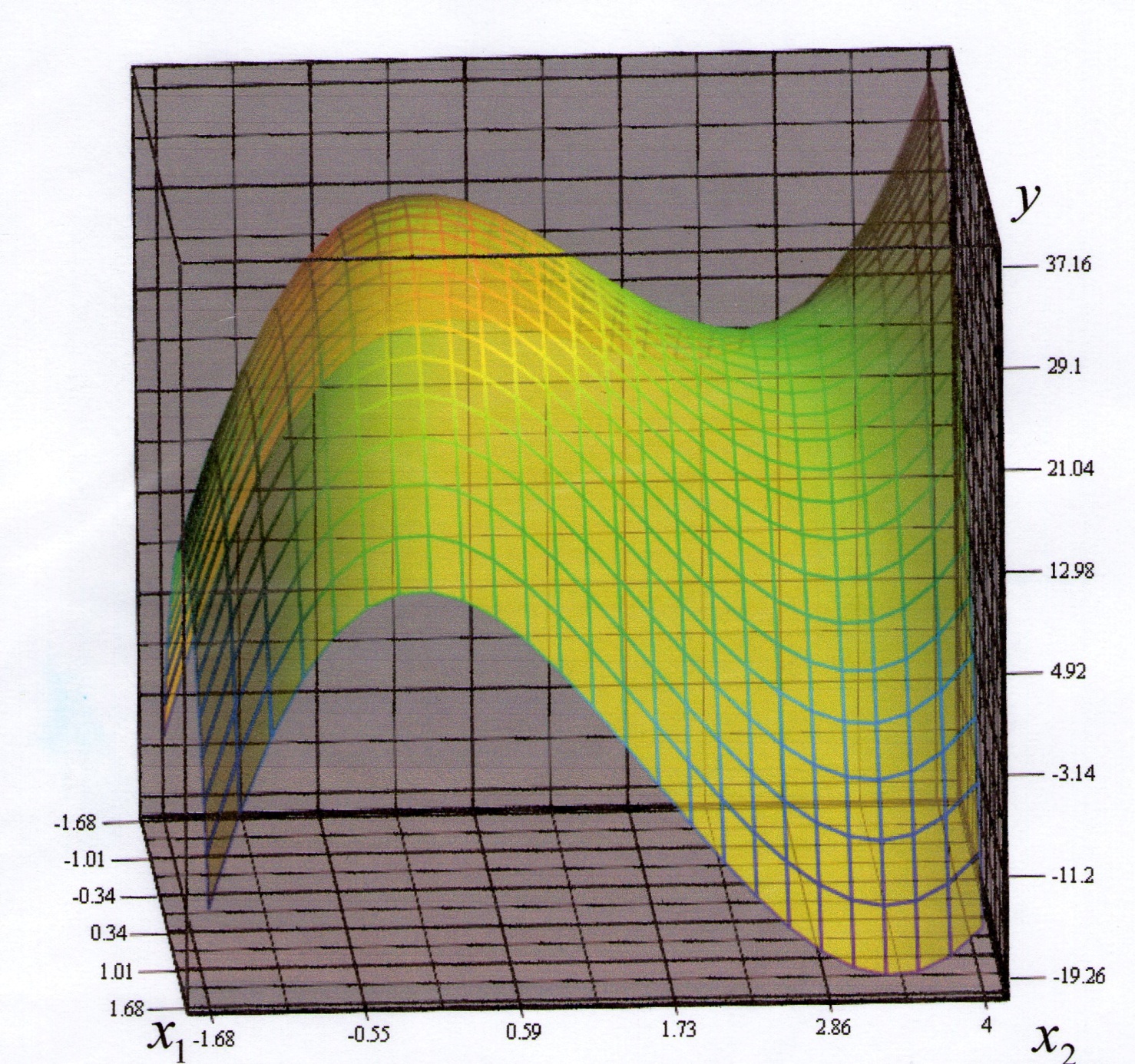
- •2. Просторова трьохвимірна область планування для кодованих значень незалежних змінних у трьохфакторному дослідженні.
- •Похибки в дослідах та ефективність моделі
2. Просторова трьохвимірна область планування для кодованих значень незалежних змінних у трьохфакторному дослідженні.

Розрахунок формул для знаходження коефіцієнтів регресії трьохфакторного поліномінального рівняння другого порядку виду:
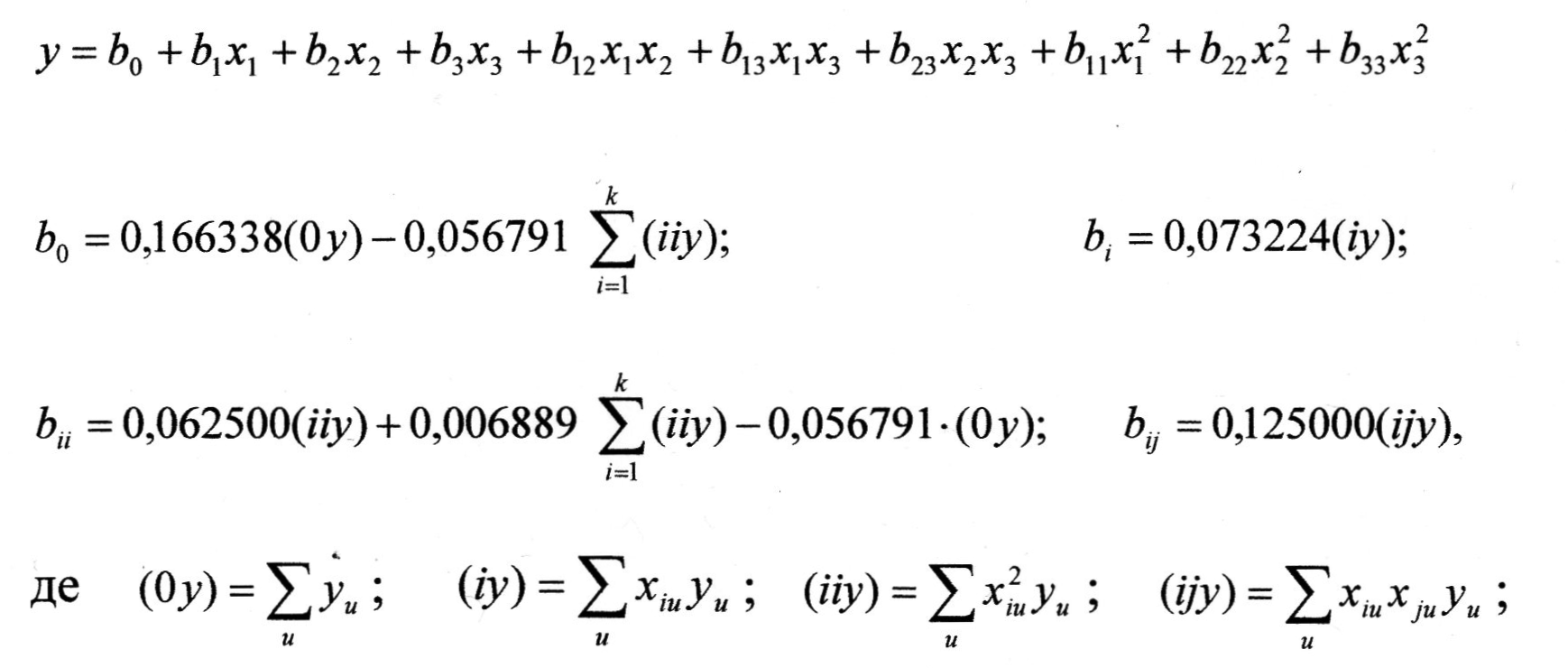
Розрахунок формул для знаходження коефіцієнтів регресії чотирьохфакторного поліномінального рівняння другого порядку виду:
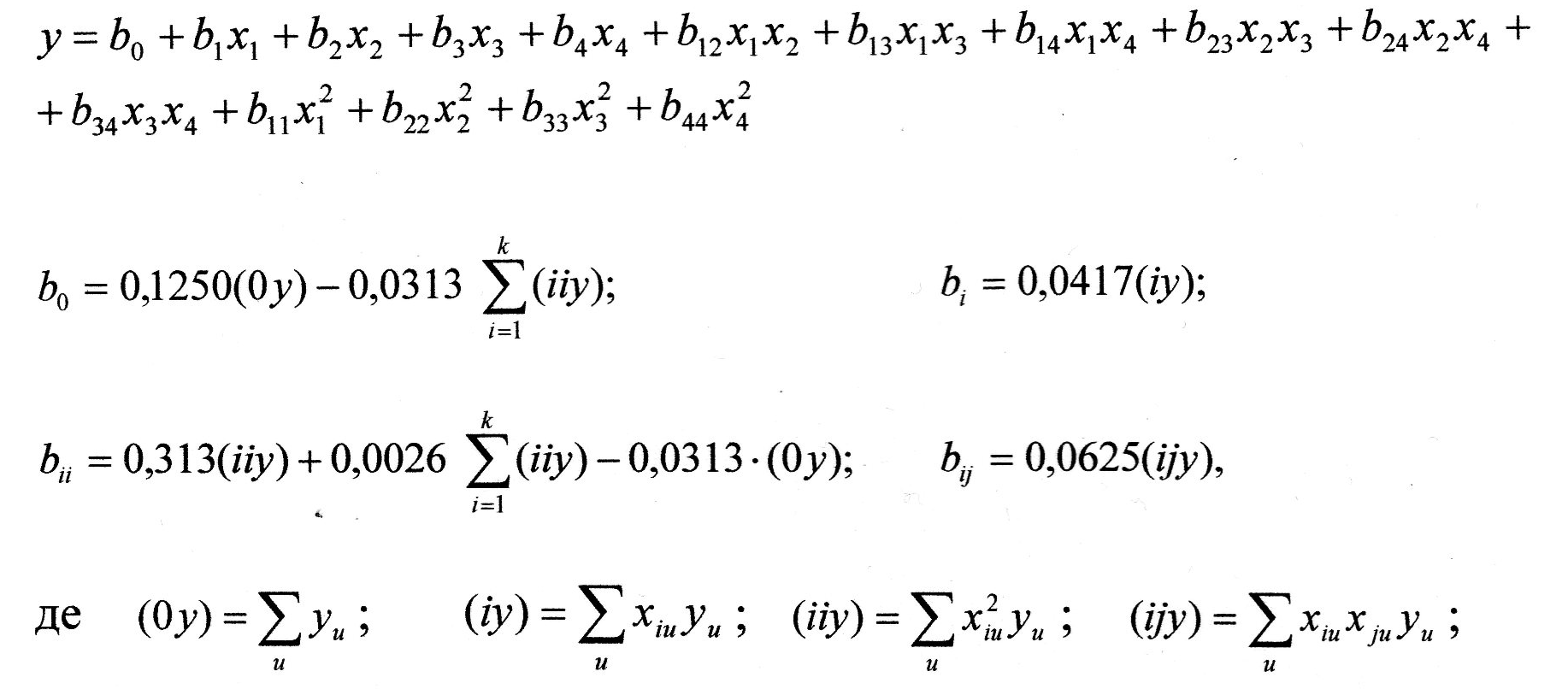
Похибки в дослідах та ефективність моделі
Нехай ми побудували модель і отримали рівняння регресії:
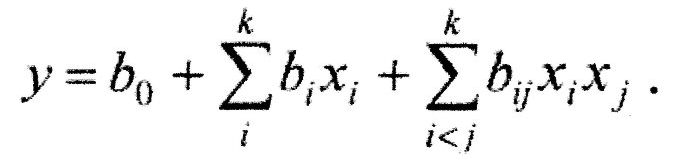
де к - число факторів.
В подальшому ми знайшли коефіцієнти регресії bi як для кодованих, так і для реальних значень факторів. Тепер виникає питання придатності цієї чисто математичної моделі для опису тієї чи іншої конкретної досліджуваної системи (економічної, фізичної, хімічної чи біологічної...). Вирішенням такого своєрідного конфлікту між математикою та реальною дійсністю є перевірка адекватності побудованої моделі. Парадокс ситуації полягає в тому, що одна і та сама модель для однієї системи може бути адекватною, а для іншої - ні. Отже, потрібно розглядати не тільки передбачувані моделлю і відповідні їм експериментальні значення досліджуваних параметрів, тобто модулі:
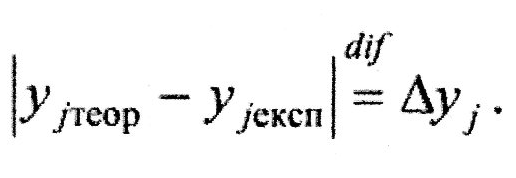
Цього недостатньо. Для повного опису необхідно проаналізувати ще і величини, які характеризують повторюваність або точніше відтворюваність результатів експерименту. Відтворюваність результатів експерименту характеризується розкидом проведених в одній і тій ж точці факторного простору дослідів, відносно їх середнього значення. Мова іде про чисельні значення параметрів в цих дослідах. Цілком очевидно, що проводячи досліди в одній і тій ж точці факторного простору, ми ніколи не отримаємо співпадаючих (тобто тотожних) результатів, оскільки кожен дослід містить елемент невизначеності і тому існує так звана помилка паралельних дослідів.
Досліди проведені в одній і тій ж точці факторного простору називають паралельними. Провівши п паралельних дослідів, ми отримаємо п значень параметра оптимізації: y1, y2,… yn .Тоді середнє значення параметра yj цих дослідах визначається формулою:
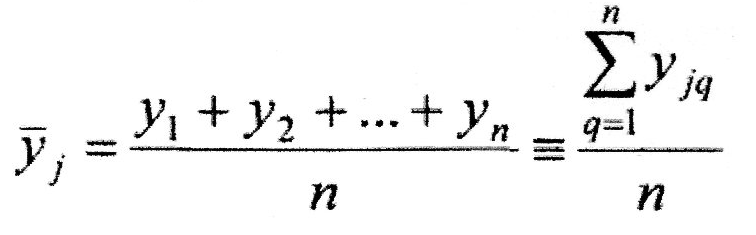
Даною
формулою можна користуватись тільки
тоді, коли чисельні значення результатів
дослідів задовольняють так званому
нормальному розподілу, тобто при
відсутності осциляцій. Наявність різких
відхилень свідчить про появу так званих
грубих спостережень і як наслідок
порушення нормального розподілу. В
таких випадках дані конкретні досліди
потрібно здійснити ще раз, або ж просто
їх не враховувати, пам'ятаючи при цьому,
що тепер уже n=n-nбраку
(що
потрібно врахувати при розрахунку
 Мірою
Мірою
варіації
(тобто наявності різних значень) параметра
оптимізації в паралельних дослідах є
так звана
 - дисперсія відтворюваності. Це статистична
характеристика, яка описує
відтворюваність результатів дослідів
в досліджуваній системі і не має ніякого
відношення до побудованої моделі.
Дисперсія відтворюваності описується
формулою:
- дисперсія відтворюваності. Це статистична
характеристика, яка описує
відтворюваність результатів дослідів
в досліджуваній системі і не має ніякого
відношення до побудованої моделі.
Дисперсія відтворюваності описується
формулою:
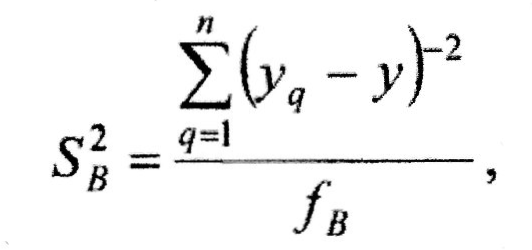
де fВ – число степенів вільності.
Для
(для
 буде іншим!),
а
в чисельнику
-
сума квадратів відхилень паралельних
дослідів від їх середнього значення.
Очевидно, що брати просто суму відхилень,
математично не коректно, оскільки
відхилення
буде іншим!),
а
в чисельнику
-
сума квадратів відхилень паралельних
дослідів від їх середнього значення.
Очевидно, що брати просто суму відхилень,
математично не коректно, оскільки
відхилення
 присутні з протилежним знаком, і тому,
навіть при значних розкидах
їх
сума
може
бути близька до нуля, а тому зовсім не
характеризуватиме відтвореність
результатів дослідів.
присутні з протилежним знаком, і тому,
навіть при значних розкидах
їх
сума
може
бути близька до нуля, а тому зовсім не
характеризуватиме відтвореність
результатів дослідів.
Модуль кореня квадратного з дисперсії називається:
І) або середнім квадратним відхиленням
II) або квадратною помилкою
III) або стандартом
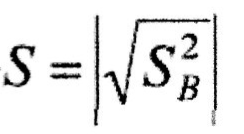
Числом степенів вільності f в статистиці називається різниця між числом дослідів і числом констант (чи коефіцієнтів), які уже обраховані за результатами цих дослідів незалежно одна (константа) від одної.
Дисперсія
адекватності
 характеризує
придатність даної конкретної моделі
для опису досліджуваного об'єкта і
знаходиться за формулою:
характеризує
придатність даної конкретної моделі
для опису досліджуваного об'єкта і
знаходиться за формулою:
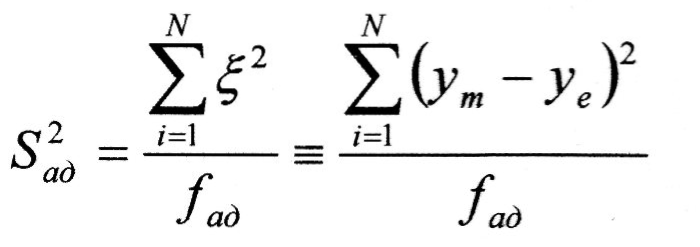
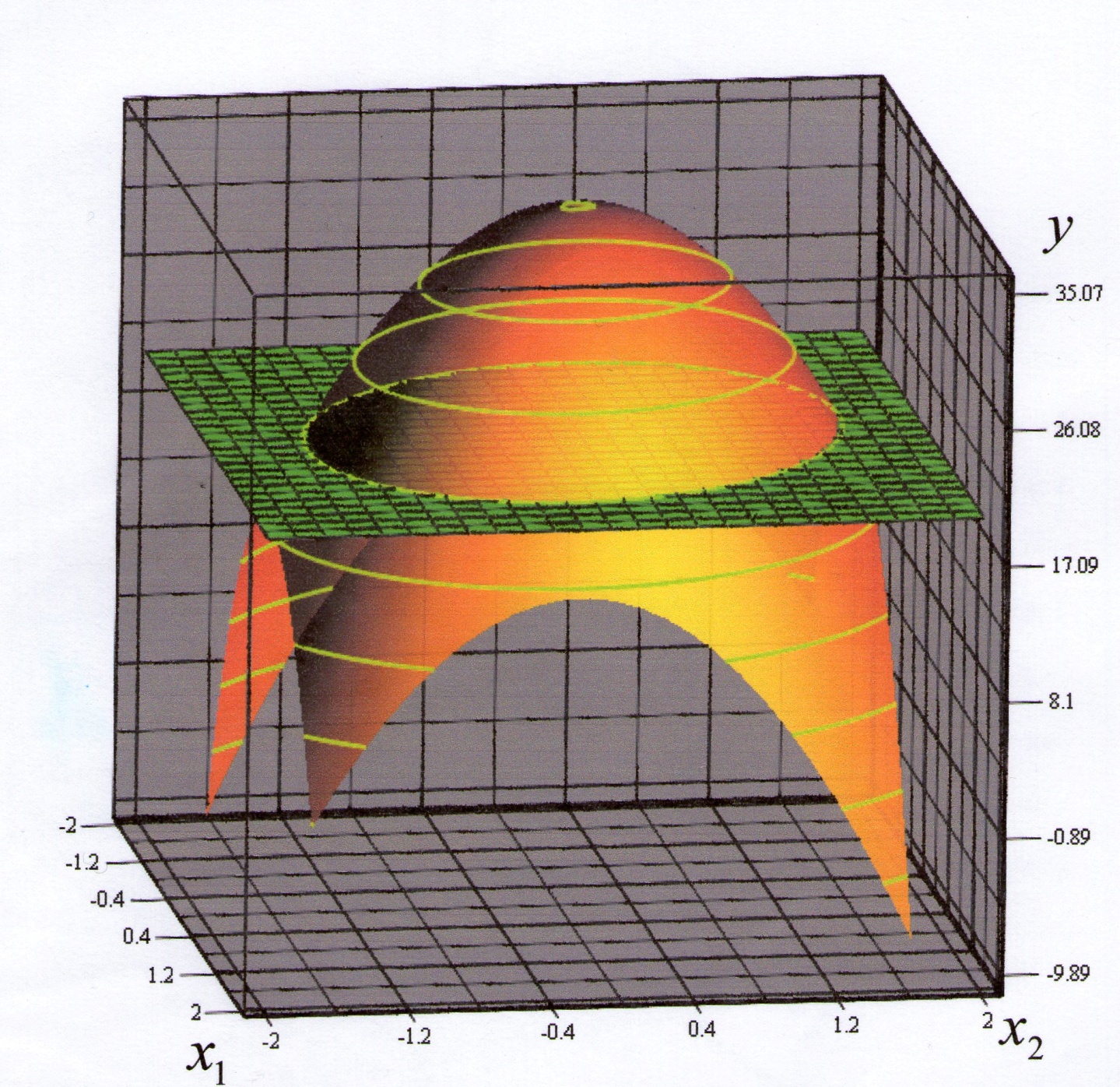
Адекватність моделі перевіряється за критерієм Фішера:
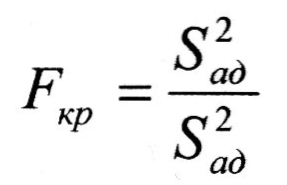
Модель адекватна, якщо одне значення Fкр не перевищує граничного значення: