Часть 2. Логический вывод и элементарные теории
2.1 Логический вывод
Введенное нами определение логического следования не дает непосредственного способа выяснения, следует ли логически та или иная формула из множества формул Γ. В математической практике для выяснения справедливости такого рода утверждений используются доказательства. Любое доказательство можно рассматривать как некоторую систему утверждений, каждое из которых либо с очевидностью является истинным, либо следует из уже доказанных утверждений. Опираясь на эти интуитивные представления о сущности доказательств, мы введем формальные понятия теории доказательств. Такими понятиями будут понятие правила вывода, доказательства, теоремы, непротиворечивости множества предложений и т. п.
Чтобы иметь представление о правилах вывода, рассмотрим следующую ситуацию. Допустим, в некотором естественном математическом доказательстве на некотором этапе мы доказали утверждение A, затем доказали, что из A следует утверждение B, тогда мы делаем вывод, что истинно утверждение B. Считая A и B предложениями логического языка, можно возвести такую ситуацию в ранг правила, по которому из истинности предложений (посылок) A и [A→B] можно в качестве заключения вывести истинность предложения B. Такое правило можно записать в виде
где над чертой выписаны формулы-посылки, а под чертой формула-заключение. Приведенное выше правило популярно во многих логических исследованиях и имеет средневековое название «модус поненс».
Мы будем рассматривать такие правила вывода, в которых заключением является не одна единственная формула, а несколько, при этом будем отличать случай, когда выводится одновременная истинность всех формул заключения, от случая, когда выводится утверждение о том, что истинна хотя бы одна из формул заключения. В первом случае будем записывать формулы заключения под чертой в виде столбца, а во втором в виде строки, в которой формулы отделены друг от друга вертикальными черточками. Правила второго вида будем называть разветвляющими.
Примеры правил вывода:
a)
,
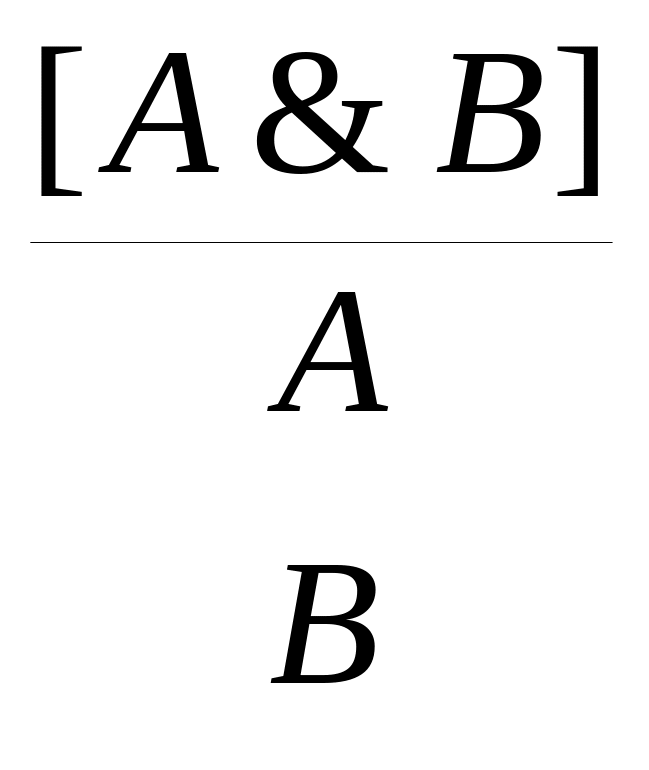б)
, в)
, г)
,
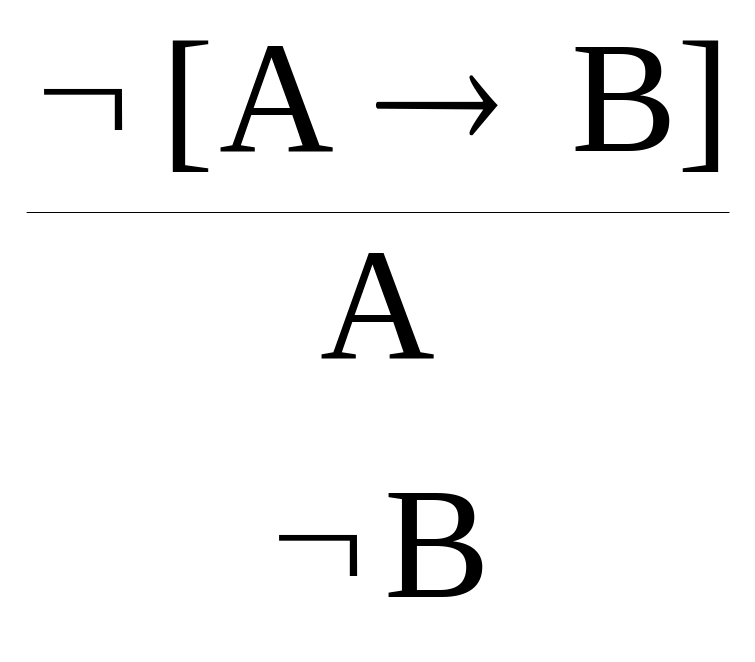где A и B произвольные предложения логического языка.
Очевидно, посылки и заключения в приведенных примерах связаны, соответственно, следующими отношениями:
а) [A&B] A и [A&B] B,
б) [A→B] ¬A или [A→B] B,
в) [AB] A или [AB] B,
г) ¬[A→B] A и ¬[A→B] ¬B.
Эти отношения говорят о том, что приведенные правила корректны. Заметим, что если в правилах б) и в) в качестве A и B употребить формулы со свободными переменными, то корректность нарушится.
Одним из основных вопросов математической логики является вопрос существования и выбора правил вывода, с помощью которых можно было бы доказать любые истинные утверждения вида ΓA, где A некоторое предложение, а Γ множество предложений, и были бы недоказуемы ложные утверждения такого вида; при этом слову «доказать» должен быть приписан четкий математический смысл.
Ниже мы покажем, что в логике предикатов
существует конечное число правил вывода
и такое математическое определение
доказательства, для которых Γ
A
тогда и только тогда, когда существует
доказательство предложения A из
множества посылок Γ. Для простоты
рассмотрим случай, когда σ не содержит
равенства и функциональных символов.
Чтобы зафиксировать набор правил вывода, заметим сначала, что любое предложение логического языка с исключающими кванторами, если оно не атомарно и не является отрицанием атомарного, имеет один из следующих одиннадцати видов:
[A&B], [AB], [A→B], (x| α) C, (x| α) C,
¬ [A&B], ¬ [AB], ¬ A→B], ¬ (x| α)C, ¬ (x| α)C, ¬ ¬ A,
где A, B предложения, C формула с единственной свободной переменной x, α состоящий из констант список исключений. Соответственно этому, в таблице 1 приведены одиннадцать правил вывода, где через Cx[a] обозначен результат подстановки константы a в формулу C вместо переменной x. Логические связки, указанные в скобках рядом с правилами, можно использовать как названия соответствующих правил.
Таблица 1
(&) 
(¬&)
() 
(¬ )
(→) 
(¬ →)
() 
(¬)
() 
(¬)
(¬ ¬)
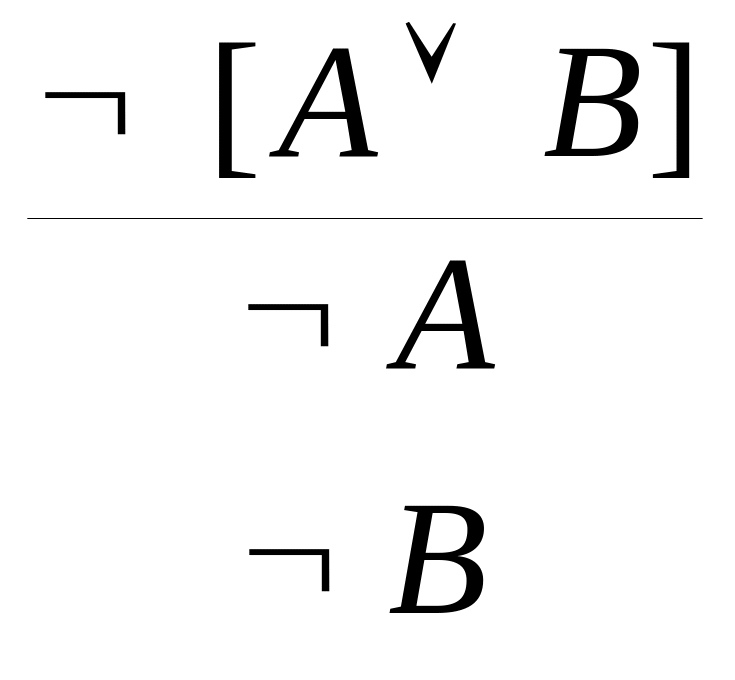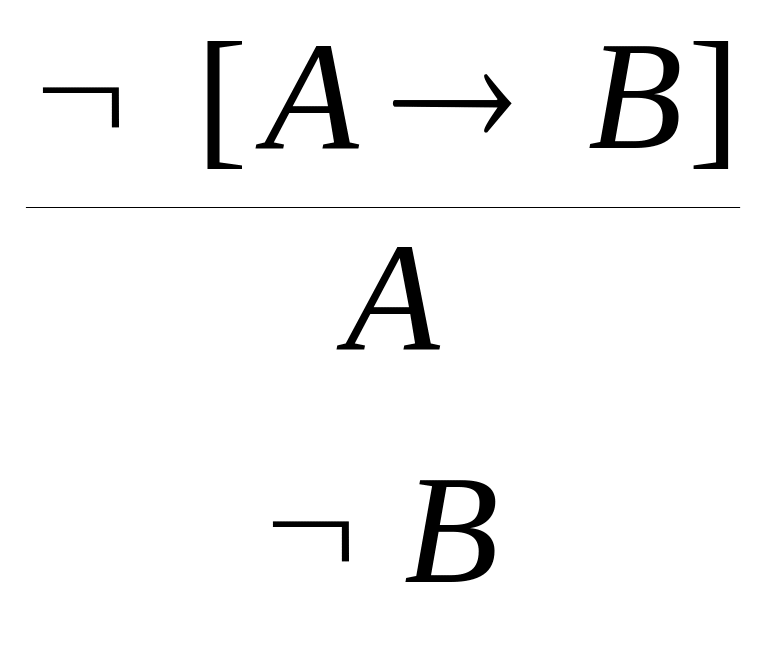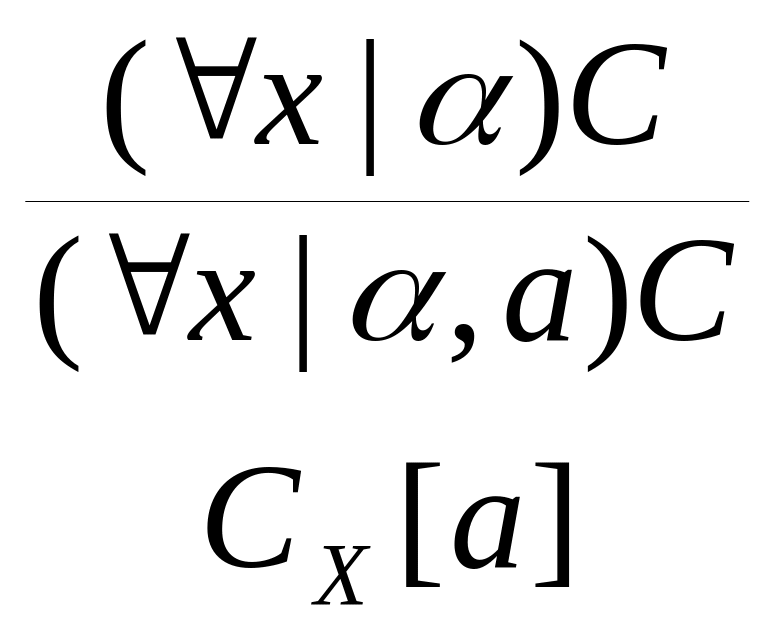Теперь рассмотрим вопрос о том, как строить доказательства с помощью перечисленных правил вывода. Естественные математические доказательства можно разделить на два класса: прямые и косвенные, например, доказательства от противного. В математической логике нет необходимости использовать оба этих варианта. Мы покажем, что можно, например, обойтись только понятием доказательства от противного. Рассмотрим предварительно два примера.
Пример 1. Выясним, является ли предложение z [S (z) & ¬P (z)] логическим следствием предложений x [P (x) → ¬M(x)] и y [S (y) & M (y)]?
Предположим, что не является, тогда существует некоторая интерпретация I с областью U, в которой истинны формулы-посылки
1. y [S (y) & M (y)],
2. x [P (x) → ¬M (x)]
и истинно отрицание формулы-заключения
3. ¬z [S (z) & ¬P (z)].
Формула 1 утверждает, что существует некоторый элемент из U (введем для его обозначения константу a), для которого истинна формула
4. [S (a) & M (a)].
Формула 2 утверждает, что для всех элементов, в том числе и для a, выполняются формулы
5. [P (a) → ¬M (a)],
6. (x|a) [P (x) → ¬M (x)].
Из истинности формулы 3 следует истинность формулы
7. z ¬ [S (z) & ¬P (z)].
Из истинности формулы 4 следует истинность формул
8. S (a),
9. M (a).
Из истинности формулы 5 следует, что возможны два случая.
В первом случае утверждается истинность формулы
10.1. ¬P (a),
а во втором случае истинность формулы
10.2. ¬M (a).
Но формула 10.2 противоречит формуле 9, поэтому остается только анализировать первый случай. Формулу 6 пропускаем, а из истинности формулы 7 выводим истинность формул
11.1. ¬ [S (a) & ¬ P (a)],
11.2. (z|a) ¬ [S (z) & ¬P (z)].
Формулы 8, 9, 10.1 пропускаем. Формула 11.1 может быть истинна, когда истинна формула
12.1.1. ¬S (a) или истинна формула
12.1.2. ¬¬P (a).
Но 12.1.1 противоречит формуле 8, а 12.1.2 формуле 10.1. Итак, сделанное нами предположение приводит к противоречию, следовательно,
{x [P (x) → ¬M (x)], y [S (y) & M (y)]} z [S (z) & ¬P (z)].
Опуская комментарии, приведенное выше доказательство можно представить в виде дерева (рис.5), узлам которого приписаны формулы. Черта в конце ветви означает, что ветвь содержит противоречие.
Пример 2. Пусть требуется определить, является ли предложение z [P (z) & ¬S (z)] логическим следствием предложений x [P (x) & ¬M (x)] и y[¬S (y) & M (y)].
Строя рассуждения по образцу предыдущего примера, получим дерево, изображенное на рисунке 6.
y [S (y) & M (y)] первая посылка
↓
x [P (x) → ¬M (x)] вторая посылка
↓
¬z [S (z) & ¬P (z)] отрицание заключения
↓
[S (a) & M (a)] из (1)
↓
[P (a) → ¬M (a)] из (2)
↓
(x|a) [P (x) → ¬M (x)] из (2)
↓
7 z ¬[S (z) & ¬P (z)] из (3)
↓
8 S (a) из (4)
↓
9 M (a) из (4)
______↓___________
↓ ↓
10.1 ¬P (a) 10.2 ¬M (a) из (5)
↓
11.1 ¬ [S (a)& ¬P (a)] из (7)
↓
12.1 (z|a) ¬[S (z)& ¬P (z)] из (7)
______↓_______________
↓ ↓
12.1.1 ¬ S (a) 12.1.2 ¬¬P (a) из (11.1)
↓
12.1.3 P (a) из (12.1.2)
Рис.5
x [P (x) & ¬M (x)] первая посылка
↓
y [¬S (y) & M (y)] вторая посылка
↓
¬z [P (z) & ¬S (z)] отрицание заключения
↓
[P (a) & ¬M (a)] из (1)
↓
[¬S (b) & M (b)] из (2)
↓
z ¬[P (z) & ¬S (z)] из (3)
↓
7 P (a) из (4)
↓
8 ¬ M (a) из (4)
↓
9 ¬ S (b) из (5)
↓
10 M (b) из (5)
↓
11 ¬ [P (a) & ¬S (a)] из (6)
↓
12 ¬ [P (b)& ¬S (b)] из (6)
↓
13 (z|a, b) ¬[P (z) & ¬S (z)] из (6)
______↓_____
↓ ↓
14 ¬P (a) 15 ¬¬S (a) из (11)
______↓_____
↓ ↓
16 ¬P (b) 17 ¬¬S (b) из (12)
↓ ↓
18 S (a) 19 S (a) из (15)
↓
20 S (b) из (17)
Рис. 6
При построении этого дерева мы ввели два параметра: a на шаге 4 и b на шаге 5. В итоге пришли к дереву, в котором все формулы, кроме формулы 13, не являющиеся атомарными или отрицаниями атомарных, использованы для расширения дерева. При этом ветвь, заканчивающаяся формулой 18, не содержит противоречия. Выбирая все атомарные формулы и отрицания атомарных формул, входящие в эту ветвь, получим список предложений
S (a), ¬P (b), M (b), ¬S (b), ¬M (a), P (a).
Используя эти предложения, легко построить структуру на универсуме {a, b}, в которой посылки истинны, а заключение ложно. Эту структуру зададим с помощью таблицы
-
x
P(x)
M(x)
S(x)
a
1
0
1
b
0
1
0
Легко проверить, что она удовлетворяет требуемому условию. Наличие такой структуры говорит о том, что предложение z [P (z) & ¬S (z)] не является логическим следствием предложений x [P (x) & ¬M (x)] и y [¬S (y) & M (y)]. Такие структуры называют контрмоделями.
Пусть Γ множество предложений сигнатуры σ и A некоторая формула той же сигнатуры.
Для доказательства утверждений вида Γ A или поиска контрмоделей для таких утверждений будем строить поисковые корневые деревья, узлы которых будем помечать формулами сигнатуры σ D, где D = {a1, a2, ...} счетное множество констант, такое, что σ D = Ø. Для простоты будем предполагать, что σ своих констант не имеет. Константы из D будут использоваться при применении (, )-правил к узлам дерева; будем называть их параметрами.
Последовательность узлов, а также приписанных им формул, от корня до концевого узла будем называть ветвью. Ветвь назовем блокированной, если она содержит некоторую формулу B и ее отрицание ¬B.
Определение поискового дерева для утверждения Γ A дадим с помощью правил его построения.
(П1) Дерево, состоящее из одного узла, помеченного формулой ¬A, является поисковым деревом с корнем ¬A. Единственный узел этого дерева считаем неиспользованным.
(П2) Если в дереве есть неиспользованный узел v, которому приписана формула, являющаяся посылкой одного из правил вывода, то с помощью этого правила каждая неблокированная ветвь W, проходящая через узел y, расширяется следующим образом:
если правило разветвляющее, то из концевого узла ветви W проводятся две дуги, оканчивающиеся новыми вершинами, которым приписываются формулы-заключения данного правила;
если правило, соответствующее узлу v, не разветвляющее, то к концевому узлу ветви W присоединяются последовательно один к другому новые узлы, помеченные формулами-заключениями.
Уточнения требуют случаи применения правил () и () поскольку они связаны с выбором параметра a. При использовании правила () в качестве a выбирается параметр с наименьшим номером, не входящий в список исключений в посылке данного правила. При использовании правила () выбирается параметр с наименьшим номером, не встречающийся в расширяемой ветви, в том числе и в списке α. После расширения дерева считаем узел v использованным, а вновь построенные узлы – неиспользованными.
(П3) Дерево также можно расширить, добавляя к концевым узлам неблокированных ветвей новый узел, помеченный очередной формулой из множества Γ или формулой вида [A ¬A], и считать его неиспользованным.
Очевидно, с помощью правил П1П3
поисковое дерево для утверждения Γ A
определяется неоднозначно. С помощью
сформулированных правил для любого
утверждения вида Γ A
может быть построена, вообще говоря,
неоднозначно, последовательность
T1, T2, ... поисковых
деревьев, в которой дерево T1
построено по правилу П1, а каждое следующее
получено из предыдущего по одному из
правил П2 или П3. Любую такую последовательность
будем называть поисковой. Если она
бесконечна, то
также будем называть поисковым деревом.
Лемма (о поисковых последовательностях). Пусть T1, T2, ... последовательность поисковых деревьев для утверждения Γ A и Di множество параметров, используемых в дереве Ti, i = 1, 2, ... . Если существует интерпретация I сигнатуры σ на универсуме U, в которой истинны все формулы из множества Γ и формула ¬A, то для каждого i = 1, 2, ... существует интерпретация Ii сигнатуры σ Di, являющаяся расширением I, такая, что в Ti есть ветвь, все формулы которой истинны в интерпретации Ii.
Доказательство. Для i = 1 утверждение леммы очевидно. Пусть существует интерпретация Ii-1 сигнатуры σ Di-1, являющаяся расширением интерпретации I, такая, что в Ti-1 есть ветвь W, все формулы которой истинны в Ii-1, и пусть Ti получено из Ti-1 применением некоторого правила вывода к узлу v.
Если vW, то ветвь W будет искомой ветвью и в дереве Ti. При этом интерпретация символов из множества Di\Di-1, если такие есть, может быть произвольной.
Пусть теперь vW. Если v имеет вид (x| α) C, и Di = Di-1, то формулы, присоединяемые к концевой вершине ветви в соответствии с правилом вывода, будут истинны в интерпретации Ii = Ii-1. Если же Di получено из Di-1 добавлением нового параметра a, то берем в качестве a(I) произвольный элемент из U, тогда присоединяемые к W формулы Cx[a] и (x| α, a) C будут истинными в полученной интерпретации Ii.
Пусть теперь v имеет вид (x| α) C и при этом Di получено из Di-1 добавлением параметра a. Поскольку формула (x| α) C истинна в интерпретации Ii-1, то существует интерпретация I', совпадающая с Ii-1 всюду, кроме возможно переменной x, такая, что C(I’) = 1. Положим a(I) = x(I’), и тогда присоединяемая к W формула Cx[a] будет истинной в Ii. Рассмотрение остальных способов расширения дерева предоставляем читателю.
Если все ветви поискового дерева, построенного для ΓA, блокированы, то такое дерево называется доказательством (в виде дерева) формулы A из посылок (гипотез) Γ. Заметим, что такое дерево нельзя расширить с помощью сформулированных выше правил П1-П3.
Если для утверждения Γ A существует дерево-доказательство, то будем говорить, что формула A выводима из множества гипотез Γ, и обозначать Γ A. Основанием для такого определения служит следующая теорема.
Теорема (о корректности дедуктики). Если Γ A, то Γ A.
Доказательство. Пусть Γ A и T соответствующее дерево-доказательство. Если бы A логически не следовала из Γ, то существовала бы интерпретация I сигнатуры σ, в которой были бы истинны все формулы из множества Γ и формула ¬A. Но тогда по лемме о поисковой последовательности существовала бы ветвь в дереве T, все формулы которой были бы истинны в некотором расширении интерпретации I, что противоречит тому, что в T все ветви блокированы. Теорема доказана.
Ветвь W называется насыщенной относительно множества D' D, если:
вместе с любой посылкой любого разветвляющего правила она содержит хотя бы одну заключительную формулу данного правила,
вместе с любой посылкой не разветвляющего правила она содержит все заключительные формулы данного правила,
она содержит каждую формулу из множества Γ.
Уточнения, как и прежде, требуют правила () и (), а именно, если формула (x| α) C принадлежит ветви W, то для любого aD' формула Cx [a] также ей принадлежит; если формула (x| α) C принадлежит W, то, по крайней мере, для одного a D' формула Cx [a] принадлежит W.
Поисковое дерево называется полным относительно множества параметров D', если любая его ветвь, либо насыщена относительно D', либо блокирована.
Лемма (о существовании полного дерева). Для любого утверждения вида Γ A существует полное поисковое дерево.
Доказательство. Уточним правила построения поисковых деревьев следующим образом. В правиле П2 в качестве v будем выбирать узел минимальной глубины, удовлетворяющий остальным требованиям. Если хотя бы одно из правил П2 и П3 применимо, то обязательно его применяем.
Используя уточненные правила, либо
через конечное число шагов получим
дерево, в котором каждая ветвь блокирована
или насыщена, либо процесс будет
продолжаться бесконечно, тогда объединение
,
где
дерево, полученное на i-ом шаге, будет
искомым деревом, в котором каждая
бесконечная ветвь будет насыщенной, а
каждая конечная будет блокированной
или насыщенной.
Теорема (о полноте дедуктики). Если Γ A, то Γ A.
Доказательство. Пусть формула A не выводима из множества Γ, тогда полное дерево T для утверждения Γ A содержит, по крайней мере, одну неблокированную насыщенную ветвь W. Пусть D' список параметров, входящих в эту ветвь (он может быть как конечным, так и бесконечным).
Рассмотрим D' в качестве универсума и зададим интерпретацию I сигнатуры σ на D' следующим образом. Для k-местного предикатного символа R σ положим
R(I)={(a1, a2, …, ak)| «R(a1, a2, …, ak)»W}.
Легко доказать индукцией по построению формулы, учитывая правила построения дерева, что при такой интерпретации все формулы, входящие в ветвь W, будут истинными. В том числе будут истинны все формулы из множества Γ и формула A, следовательно, A логически не следует из Γ.
Объединяя теоремы о корректности и полноте, получим следующую теорему.
Теорема (об адекватности дедуктики). Γ A тогда и только тогда, когда Γ A.
Теорема (о компактности). Если Γ A, то существует конечное подмножество Γ' Γ такое, что Γ' A.
Действительно, пусть Γ A, тогда по теореме о полноте Γ A, следовательно, существует дерево-доказательство, в котором все ветви блокированы и, следовательно, конечны. Следовательно, число гипотез из Γ, содержащихся на этих ветвях, конечно, они и образуют требуемое конечное подмножество гипотез.
Упражнения. Построить поисковые деревья для следующих утверждений:
а) {x [P (x) →y R (x, y)], x y R (x, y), x [P (x) →Q (x)]}
x [Q (x) & y R (x, y)];
б) {x [P(x) → y R(x,y)], x y R(x, y)} x [P(x)&yR(x, y)];
в) {x [Q (x) → y [S (y) & R (x, y)]], xyz [R (x, y) & R (y, z) → R (x, z)],
x [P (x) & y [S (y)R (x, y)]]} x[P (x) & y[Q (y) R (x, y)]];
г) {x [P (x) →Q (x)], xy [R (x, y) → P (x)&Q (y)]} xy [Q (x) & P (y) → R (x, y)];
д) {x [P (x) →Q (x)R (x)S (x)], x [Q (x) → P (x) R (x) S (x)]}
x [R (x) & Q (x) → S (x)];
е) {x [P (x) & y [S (y) → R (x, y)]], x [P (x) → y [Q (y) → R (x, y)]]}
x [S (x) → Q (x)];
ж) xy [R (y, x) & z [R (x, z) → R (y, z)]] x R (x, x);
з) {x y R (x, y), xyz [R (x, y)&R (y, z) →R (x, z)]}
xy [R (x, y)&R (x, y)];
и) {x [S (x) → P (x) & Q (x)], xy [R (x) T (y) → S (x) & P (x)]}
xy [R (x) & T (y)&P (x) → Q (x)];
к) {x [S (x) → P (x)], x[R (x) →T (x)], x[P (x) & T (x) → Q (x)]}
x [S (x) & R (x) → Q (x)];
л) {x [S (x) → P (x)], x [R (x) → T (x)], x [P (x) & T (x) → Q(x)]} x [S (x) & R (x) → Q (x)].
Упражнения. Построить поисковые деревья для следующих утверждений:
