МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

ІМЕНІ ЮРІЯ КОНДРАТЮКА

КАФЕДРА НАРИСНОЇ ГЕОМЕТРІЇ ТА ГРАФІКИ

Методичні вказівки

До виконання розрахунково-графічних робіт

Із спецкурсу інженерної графіки

Для студентів будівельних спеціальностей

Полтава 2005

Методичні вказівки до виконання розрахунково-графічних робіт із спецкурсу інженерної графіки для студентів будівельних спеціальностей. – Полтава: ПолтНТУ‚ 2005. – 27 с.

Укладачі: В.Г. Усенко‚ канд. техн. наук‚ доцент;

О.А. Кодак‚ канд. техн. наук‚ доцент

Відповідальний за випуск : завідувач кафедри нарисної геометрії та графіки О.В. Воронцов‚ канд. техн. наук‚ доцент

Рецензент: Д.Ф. Погорілий‚ канд. техн. наук‚ доцент

Затверджено радою університету

протокол № 1 від 27.10.2005 р.

Редактор Н.В. Жигилій

Коректор Н.О. Янкевич

ВСТУП

Необхідність розроблення даного комплексу завдань викликана включенням до курсу графічних дисциплін нових розділів "Обчислювальна геометрія" й "Машинна графіка".

Розроблений комплекс розрахунково-графічних робіт передбачає знання студентами основного курсу нарисної геометрії. Комплекс охоплює теми: “Інтерполяція” та “Дискретне моделювання кривих ліній і поверхонь”. Завдання складені так, щоб студенти засвоїли найбільш розповсюджені на практиці методи й алгоритми конструювання криволінійних форм.

Усі розрахунково-графічні роботи виконуються на аркушах формату А3. Студентам слід додержуватись товщини та типів ліній, передбачених державними стандартами. Номери шрифту для оформлення робіт такі: назва роботи – №7, назви окремих частин креслень і підпис роботи – №5, позначення функцій, числові дані й т. ін. – № 3.5.

Завдання № 1. Конструювання каркаса поверхні переходу

Умова завдання

Сконструювати каркас із кривих другого порядку поверхні переходу від круглого (еліптичного) перерізу до прямокутного (квадратного).

Мета завдання – освоїти практичні прийоми використання жмутка кривих другого порядку для конструювання поверхні.

Рекомендації до виконання завдання

Завдання виконується на аркуші формату A3. Приклад виконання завдання показаний на рис. 4.

Вихідні дані для завдання наведені в табл. 1. Зміст величин, що входять у нього, пояснює рис. 1.

Проміжні перерізи будуються як обводи з кривих другого порядку, вписаних у прямокутні контури, площини котрих паралельні xOz. Останні отримані лінійною інтерполяцією вздовж осі поверхні, що збігається з віссю Oy, габаритних розмірів заданого прямокутного перерізу і прямокутника, описаного навколо криволінійного перерізу. На рис. 1 показане визначення контурів прямокутників для проміжних перерізів, яким присвоєні номери "1", "2", "3" (вихідні перерізи: "0" і "4").

За умовою задачі для всіх варіантів контур "1" – обвід з дуг еліпсів, "2" – з дуг парабол, "3" – з дуг гіпербол.

Кожна дуга обводу проміжних перерізів отримується на основі методу інженерного дискримінанта [1, п. 5.3.2]. Графічна побудова використовує встановлення взаємо-однозначної відповідності між променями двох жмутків прямих [1, п. 5.3.3].

Аналітичний опис кривих оснований на заданні однопараметричного жмутка кривих другого порядку, що належить контурові криволінійного перерізу і двом сторонам прямокутника (кривої другого порядку, що розпалася).

Рис.1

Конкретне значення параметра і відповідне рівняння визначається за допомогою додаткової точки, через яку проходить крива лінія. Загальне рівняння жмутка кривих другого порядку має вигляд:

. (1)

Знак перед другим доданком визначається областю існування жмутка кривих ліній при 0≤ λ ≤ 1. Для того, щоб крива існувала в цій області, необхідно, щоб доданки, що входять у (1), мали різні знаки.

Розглянемо це на прикладі. Нехай φ₁ – коло, φ₂ – дві прямі, що перетинаються (на рис. 2 показано четверту частину зображення). Тоді перший доданок набере вигляду

S₁=(1-λ)(х²+z²-R²),де (1-λ) >0 (за умовою).

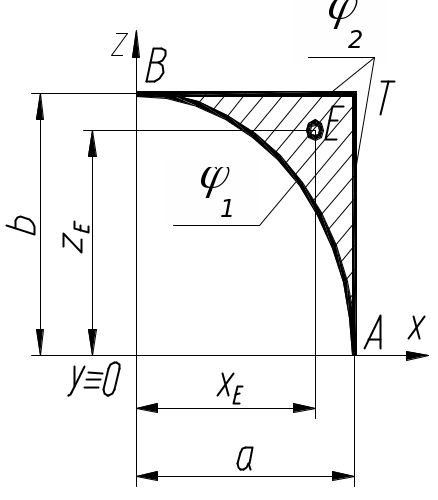
Рис. 2

Знак другого співмножника визначається підстановкою в S координат деякої точки Е (рис. 2), інцидентної області існування жмутка кривих (на рисунку – заштрихована) і R=a:

,

тоді S₁>0 Другий доданок: S₂=(x - a)(z – b) (на рис. 2, a=b).

Підставивши x_E, y_E в S₂ , одержимо;

x_E - а<0, z_E – b<0,

звідки S₂>0, тобто обидва доданки мають однаковий знак, тому необхідно в (1) залишити знак "–":

. (2)

Як показано на рис. 3, дуга еліпса виділена з жмутка кривих другого порядку, заданого точками A₁, B₁ та дотичними в них А₁ T₁ і B₁ T₁ заданням додаткової точки E₁, розташованої на медіані D₁ T₁, трикутника A₁ B₁ T₁, згідно з відповідним значенням інженерного дискримінанта для еліпса. Потрібно замірити значення координат x_E1, z_E1.

При цьому для того, щоб не вийшло небажаної "вм'ятини" на поверхні, необхідно дотримуватися співвідношення ,

де E₀ – точка вихідної кривої на медіані T₀D₀ трикутника A₀T₀B₀ , отриманого за аналогією з трикутником A₁T₁B₁. Крива будується як множина точок перерізу відповідних променів жмутків прямих із носіями A₁ і B₁, при встановленні відповідності між ними за допомогою променів жмутка прямих із носієм T₁ [1, п. 5.3.3]. На рис. 3 показана послідовність графічної побудови кривої при вищевказаних умовах.

Рис. 3

Аналогічно дуга параболи виділяється з жмутка кривих (A₂B₂, A₂T₂, B₂ T₂), а дуга гіперболи – з жмутка (A₃B₃, A₃T₃, B₃ T₃ ).

Потім визначаються рівняння кожної з цих кривих. При цьому треба мати на увазі, що оскільки всі перерізи вписуються в різні прямокутники, то для складання рівняння перерізу "1" (еліпса) необхідно в (1) підставляти величини a₁, b₁; для перерізу "2" (параболи) – a₂, b₂; для перерізу "3" (гіперболи) – a₃, b₃ (див. рис. 1).

Для випадку на рис. 4 (коли перерізом "0" є еліпс) загальне рівняння жмутка кривих має вигляд:

, (3)

де p та q – піввісі еліпса.

Для перерізу "0", що має вигляд кола,

, (4)

при і = 1, 2, 3.

Із (3) або (4) визначають вираз для λ_і , а потім підстановкою у нього координат точки Е_і знаходять конкретне значення λ для кожної кривої.

Шукане рівняння кривої виходить при підстановці λ_і в (3) або (4). Після перетворень (3) та (4) представляються для еліптичного "0" перерізу так:

. (5)

Для круглого "0" перерізу:

(6)

Завдання завершується побудовою фронтальної ізометрії сконструйованого каркаса поверхні.

Примітки:

1) величина i є відрізком осі поверхні, що належить 0у, між перерізами "0" і "4";

2) у варіантах 11-15 і 26-30 при складанні рівняння жмутка кривих вихідне коло розглядати як еліпс із рівними півосями a=b. Для інших перерізів a≠b.

Рис. 4