2. Влияние кривизны Земли на определение горизонтальных и вертикальных расстояний

Небольшой участок сферической поверхности при определенных условиях можно принять за плоскость. Применение модели плоской поверхности при решении геодезических задач возможно лишь для небольших участков поверхности Земли, когда искажения, вызванные заменой поверхности сферы или эллипсоида плоскостью невелики и могут быть вычислены по простым формулам. Это тем более оправдано, если учесть, что измерения на местности и чертежные работы всегда выполняются с ошибками, а потому небольшую часть сферы (эллипсоида), отличающуюся от плоскости на величину, меньшую ошибок измерений, можно считать плоской.

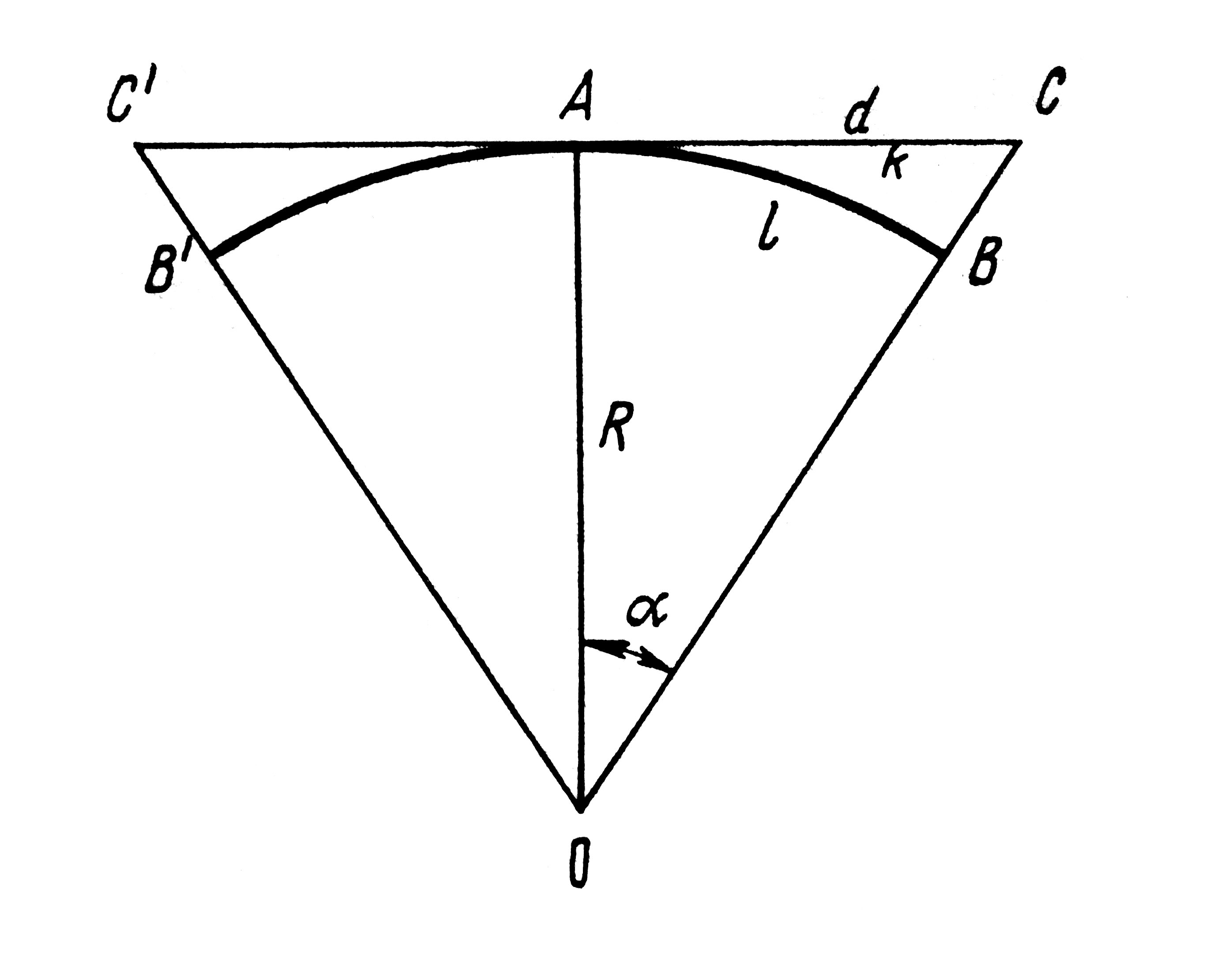
Рис. 2.2.1. Влияние кривизны Земли на определение горизонтальных и вертикальных расстояний

Рассчитаем, какое искажение получит дуга окружности, если заменить ее отрезком касательной к этой дуге.

Предположим, что на поверхности Земли измерена дуга AB, равная l. Длину касательной AC обозначим через d. Определим разность между длиной касательной и длиной кривой, которая и покажет влияние кривизны Земли на определение горизонтальных расстояний

. (2.2.1.)

Из рис. 2.2.1. видно, что

. (2.2.2.)

Так как угол  величина малая, то можно пользоваться приближенной формулой

, (2.2.3.)

где значение  выражено в радианах, тогда можно записать

или

. (2.2.4.)

Подставив значение d из формулы (2.2.4.) в формулу (2.2.1.), получим

. (2.2.5.)

Разность между длиной касательной и кривой, подсчитанная по формуле (2.2.5.), приведена ниже

l, км	10	25	50
Δd, см	0,82	12,80	103,00
Относительная ошибка	1:1200000	1:200000	1:50000

Отсюда видно, что влияние кривизны Земли на определение горизонтальных расстояний при l = 10 км составляет 1:1200000 ее длины, что допустимо при самых точных измерениях горизонтальных расстояний на земной поверхности. Вследствие этого при измерениях на площади круга с радиусом в 10 км уровенную поверхность можно считать за плоскость, а d практически равным l. Достигнутая точность измерения расстояний пока не превышает 1/1000000, поэтому при геодезических работах любой точности участок сферы 20 х 20 км² можно считать плоским. При работах пониженной точности размеры участка сферы, принимаемого за плоскость, можно увеличить.

Кривизна Земли оказывает также значительное влияние на определение вертикальных расстояний. Отрезок CB = k выражает это влияние. Определим величину этого отрезка из равенства

или

,

откуда

. (2.2.6.)

По малости k по сравнению с 2R формулу можно написать так:

. (2.2.7.)

Ниже приведены данные, показывающие влияние кривизны Земли на определение вертикальных расстояний.

d, м	100	200	300	1000	10000
k, мм	0,8	3,1	7,1	78,0	7850,0

Отсюда следует, что при определении превышений между двумя точками следует учитывать поправку на кривизну Земли.