Введение

Цель данного посо­бия помочь студенту самостоятельно подготовиться к выполнению контрольных работ. При написании пособия авторы не ставили своей целью дать систематическое изложение теоретического материала. Перед каждой рассматриваемой задачей дается тот теоретический материал, который необходим для ее решения. Если студент ранее овладел необходимым теоретическим материалом, то вводную часть каждой задачи он может опустить и перейти непосредственно к решению задачи. Необходимо отметить, что приведенный теоретический материал достаточно полно охватывает курс указанного предмета. Авторы надеются, что пособие будет полезно студентам в овладении методами решения основных задач курса теории вероятностей и математической статистики.

Глава 1. Случайные события и их вероятности §1. События. Действия с событиями

Определение. Элементарным событием называется простейший неделимый исход некоторого опыта.

Элементарные исходы будем обозначать символом .

Определение. Пространством элементарных исходов называется множество всех элементарных исходов, которое будем обозначать символом .

Рассмотрим несколько примеров.

Пример 1. Описать пространство элементарных исходов при подбрасывании монеты.

 Решение. Очевидно, что при подбрасывании монеты возможны два элементарных исхода:

— появление «герба»;

— появление «решки».

Таким образом, пространство элементарных исходов содержит два элемента

. 

Пример 2. Описать пространство элементарных исходов при подбрасывании игрального кубика.

 Решение. Очевидно, что при подбрасывании игрального кубика элементарными исходами является число, выпавших очков, т.е.

— выпало ровно очков; .

Таким образом, пространство элементарных исходов содержит шесть элементов

или . 

Пример 3. На отрезке случайным образом отмечается точка. Описать пространство элементарных исходов.

 Решение. В этом случае результатом является координата , удовлетворяющая условию . Очевидно, что координата меняется непрерывно, пространство элементарных исходов имеет вид

.

Пространство элементарных исходов имеет бесконечно много элементов. 

Определение. Событие называется достоверным, если в результате опыта оно непременно должно произойти.

Достоверное событие обозначают символом , так как оно состоит из тех же элементарных исходов, что и пространство элементарных исходов. Событие, состоящее в появлении менее 7 очков при бросании игрального кубика, является достоверным.

Определение. Событие называется невозможным, если в результате опыта оно не может произойти.

Невозможное событие обозначают символом . Событие, состоящее в появлении 7 очков при бросании игрального кубика, является невозможным.

Определение. События называют несовместными, если при наступлении одного из событий, остальные события в данном испытании наступить уже не могут.

Так, например, если при бросании игральной кости выпала грань «2», то это означает, что при том же бросании не могла появиться грань «4».

Определение. События образуют полную группу событий, если в результате опыта, одно из событий обязательно происходит.

Например, при однократном бросании игральной кости полная группа попарно несовместимых событий состоит из событий

,

которые состоят соответственно в выпадении 1,2,3,4,5,6 очков соответственно.

Наряду с элементарными событиями будем рассматривать случайные события.

Определение. Случайным событием (или просто событием ) называется любое подмножество множества .

Определение. Элементарные события, принадлежащие подмножеству , называются благоприятствующими событию .

Рассмотрим основные операции над событиями; они полностью соответствуют основным операциям над множествами.

Определение. Суммой событий и называется событие , состоящее в наступлении хотя бы одного из событий или .

Элементарными исходами суммы событий являются элементарные исходы, принадлежащие хотя бы одному из событий и .

Определение. Произведением событий и называется событие , состоящее в совместном (одновременном) наступлении этих событий.

Элементарными исходами произведения событий являются те элементарные исходы, которые одновременно принадлежат событиям и .

Определение. Разностью событий и называется событие , состоящее в том, что событие произошло, а событие не произошло.

Элементарными исходами разности событий являются те элементарные исходы события , которые не принадлежат событию .

Определение. Событие, состоящее в том, что событие не происходит, называется противоположным событию и обозначается .

Элементарными исходами противоположного события являются те элементарные исходы, которые не принадлежат событию .

Определение. Событие влечет событие ( является подмножеством множества ), если из того, что происходит событие , следует, что происходит событие ; записывают .

Определение. Если одновременно и , то в этом случае события и называют равносильными, при этом пишут .

Пример 4. Если — событие, состоящее в том, что взятое наудачу изделие первого сорта, а — изделие качественное (не брак), то в том событие влечет событие : .

Свойства операций над событиями:

• , (коммутативность);

• , (дистрибутивность);

• , (ассоциативность);

• , ;

• , ;

• , ;

• , , ;

• ;

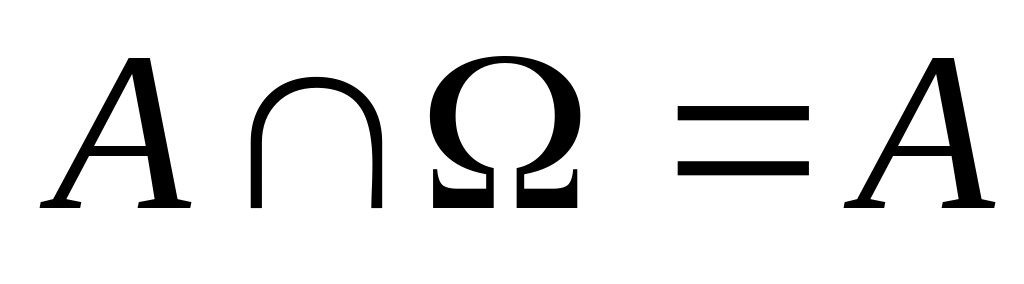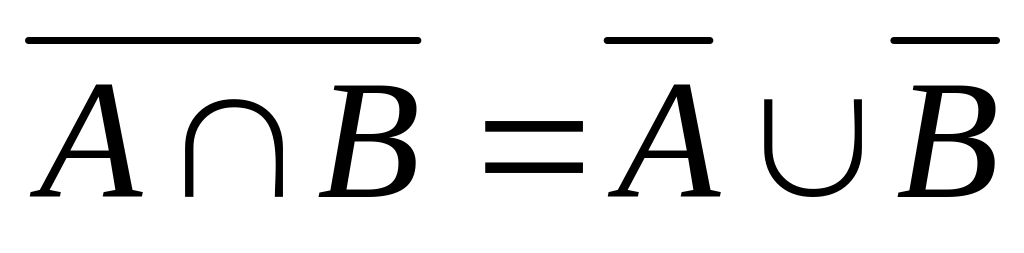• , (законы де Моргана).