
- •Метод конечных элементов.
- •Построение сетки конечных элементов
- •Создание нового макроса
- •Добавление аргументов
- •Добавление шагов процесса к макросу
- •Вставка макросов в процесс
- •Лабораторная работа № 1 "Составление описания технологического процесса формирования кмоп-инвертора"
- •Порядок выполнения работы:
- •Приложение 1. Код командного файла
- •Лабораторная работа № 2 "Составление описания технологического процесса формирования биполярного транзистора"
- •Порядок выполнения работы:
- •Формирование эпитаксиального слоя.
- •Формирование контакта к заглубленному слою.
- •Формирование базовой области транзистора.
- •Формирование эмиттерной области транзистора.
- •Формирование металлической разводки.
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им. В.И. Ульянова (Ленина)»
(СПбГЭТУ)
«Моделирование технологических процессов формирования элементов микро- и наноэлектроники»
Санкт-Петербург
2010
Введение.
Целью данного курса является ознакомление с основными понятиями в области математического моделирования, изучение основных принципов моделирования технологических процессов наноэлектроники, освоение программного пакета Synopsys TCAD. Предметом рассмотрения являются основные математические модели и методы, положенные в основу моделирования технологических процессов, целостный технологический процесс и принципы оптимизации технологических процессов с использованием математического моделирования. Важным элементом дисциплины является выработка навыков проектирования технологических циклов производства устройств наноэлектроники с заданными электрофизическими параметрами.
Материал, изложенный в лекционном курсе, и работы лабораторного практикума прошли серьезную апробацию в учебном процессе на факультете электроники Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И.Ульянова (Ленина). Технологическое моделирование – сложная интегральная дисциплина, использующая знания из нескольких областей: материаловедение полупроводников и диэлектриков, технология производства СБИС, устройств оптоэлектроники и наноэлектроники, микро- и наноэлектроника, схемотехника, численные методы и основы вычислительной техники.
В дистанционном курсе изложены основные сведения, необходимые для моделирования базовых технологических процессов, входящих в маршрут изготовления полевого транзистора с самосовмещенным поликремниевым затвором. В очной части курса предусмотрено выполнение моделирования технологического процесса и получение характеристик готового прибора с помощью программного пакета Sentaurus TCAD.
При самостоятельном изучении лекционного материала обучающимся необходимо с помощью рекомендуемой литературы освежить знания по курсам материаловедения полупроводников и диэлектриков, технологии производства СБИС (особенно тщательно должны быть проработаны процессы диффузии, окисления кремния и ионной имплантации). Самое пристальное внимание должно уделяться вопросам совместимости материалов и технологических операций в едином технологическом процессе, влиянию разброса конструкционных и технологических параметров на характеристики готовых приборов.
Программный комплекс Sentaurus TCAD снабжен достаточно простым, интуитивно понятным интерфейсом. Основные сведения о базовых модулях пакета: Sentaurus Process, Ligament, Sentaurus Device, Sentaurus Workbench, Tecplot-sv и Inspert, необходимые для начала работы с ним, изложено в лекционном курсе. Для более глубокого изучения программы обучающимся понадобиться ознакомиться с руководством пользователя (к сожалению, довольно объемные User Guide имеются только на английском языке).
Лекция 1. Целостное представление о технологическом процессе. Приборно-технологическое моделирование (TCAD). Метод конечных элементов
Целостное представление о технологическом процессе.
В основе процесса формирования элементов БИС и СБИС лежит планарно-эпитаксиальная технология, включающая в себя процессы нанесения и удаления вещества, окисления, фотолитографии, ионной имплантации и локальной диффузии. Последовательность выполнения операций и параметры проводимых процессов определяются структурой изготавливаемого прибора, условиями получения требуемой структуры и состава слоев, составляющих устройство, совместимостью и физическими свойствами материалов. Для проектирования технологического процесса недостаточно знать физико-технологические основы проведения отдельных процессов (например, нанесения слоев, диффузии или имплантации), необходимо учитывать также и влияние каждой из проводимых операций на результат всех остальных. Так, все высокотемпературные процессы приводят к перераспределению примесей, введенных в структуру на предшествующих этапах процесса, изменению количества дефектов, могут вызывать химические превращения или размытие интерфейсов за счет взаимного проникновения материалов. Учесть все многообразие факторов, влияющих на характеристики конечного изделия в процессе его изготовления, практически невозможно. В течение длительного времени разработка и отладка технологических процессов в электронике проводилась путем постановки большого числа экспериментов, изготовления опытных образцов, их тестирования и внесения корректив для оптимизации процесса с целью получения требуемых электро-физических характеристик. Этот процесс протекал месяцы, иногда годы, требовалось задействовать большое количество высококвалифицированных специалистов, помещения, оборудование, материалы.
В результате применения средств компьютерного моделирования стало возможным значительно ускорить процесс разработки и оптимизации технологических процессов изготовления новых устройств электроники, а также снизить трудовые и финансовые затраты на его осуществление.
Приборно-технологическое моделирование или TCAD (Technology Computer Aided Design) - это область научных знаний и прикладных программных инструментов, позволяющая осуществлять многомерное моделирование интегральных полупроводниковых структур, используя в качестве исходной информации описание технологического процесса их изготовления. Возможности TCAD:
- моделирование технологического маршрута;
- расчет электрических характеристик двух- и трехмерных структур;
- анализ устойчивости к технологическому разбросу и внешним воздействиям;
- планирование «виртуального» эксперимента;
- оптимизация параметров технологических операций, размеров элементов;
- экстракция схемотехнических параметров прибора, расчет фрагментов схем.
По многочисленным расчетам использование TCAD снижает стоимость полупроводникового производства на 40% за счет уменьшения числа экспериментов и сокращения затраченного времени.
Известно, что преобладающим механизмом, наносящим убыток при производстве с топологическими нормами 90 нм и менее, становятся параметрические колебания из-за повышенной чувствительности характеристик таких приборов и схем к параметрам процессов.
Быстрое и упрощенное многомерное моделирование процесс-прибор-схема позволяет проанализировать факторы, которые могут приводить к потерям в производстве, связанным с параметрическими колебаниями.
Пакет программ Sentaurus TCAD разработан фирмой Synopsys (США) при участии фирмы ISE (Швейцария) и является одним из наиболее распространенных в настоящее время (по крайней мере в России). Этот продукт ориентирован на разработчиков различных полупроводниковых приборов, таких как биполярные и МДП приборы, оптоэлектронные приборы и т.д. Пакет позволяет моделировать большинство технологических процессов, различные режимы работы приборов, в том числе и в составе схем.
Основной акцент в развитии средств приборно-технологического проектирования (TCAD) сегодня делается на следующих направлениях:
Трехмерное моделирование субмикронных приборов, включающее моделирование технологического процесса формирования структуры прибора и анализ трехмерного растекания носителей заряда;
Потребность в трехмерном моделировании современных субмикронных приборов обусловлена необходимостью анализа тонких физических эффектов в полупроводниковых структурах, для которых точности методов двумерного моделирования оказывается недостаточно. На современном уровне развития микроэлектронного производства подобные тонкие физические эффекты оказывают значительное влияние на функционирование полупроводниковых приборов. При существующих темпах совершенствования технологии, учет данных эффектов в ближайшем будущем должен играть определяющую роль.
Моделирование мощных кремниевых и гетероприборов (в том числе и на основе SiC и GaN), приборов на основе материалов А3В5, использующих гетеропереходы (НЕМТ, НВТ), фотодетекторов, светоизлучающих диодов (LED) и полупроводниковых лазеров;
Возможность построения компактных моделей (на базе результатов моделирования или измерений конкретного прибора), отражающих зависимость выходных (электрических) параметров от разброса входных (технологических) параметров. С помощью таких моделей можно определить окно значений технологических параметров, в котором обеспечиваются требуемые характеристики прибора.
В составе Sentaurus TCAD содержится большое количество различных блоков. Модели, заложенные в основу отдельных частей пакета, разработаны на основе экспериментальных данных и затем были успешно проверены при практическом проектировании различных структур, в основном, на основе кремния. В зависимости от решаемых проблем могут использоваться разные по уровню сложности и точности модели. Для широкого круга наиболее часто используемых материалов (Si, Ge, ряд соединений А3В5, SiO2 и некоторых других) при моделировании могут использоваться апробированные значения параметров материалов или моделей. Значения этих параметров в случае необходимости могут быть скорректированы или заданы пользователем, что в принципе позволяет моделировать и структуры на основе новых материалов. В случае необходимости предусмотрена возможность включения дополнительных (пользовательских) модулей, которые должны оформляться в среде языка программирования С++.
Ниже приведен далеко не полный перечень задач, которые могут быть решены средствами рассматриваемого пакета.
Моделирование технологических процессов – диффузии примесей, ионного легирования, окисления и т.д.;
Моделирование вольтамперных и иных характеристик структур, их работы при малых и больших уровнях сигналов, переходных процессов и т.д.;
Моделирование процессов взаимодействия с электромагнитным излучением, светом, излучение света, воздействия стационарных и переменных магнитных полей;
Моделирование тепловых режимов работы структур и механических напряжений в структурах;
Оптимизация параметров моделей (или приборов) по заданным критериям.
Модели, описывающие разные по своей природе процессы, могут использоваться комплексно. Например, возможен учет взаимного влияния механических напряжений и процессов диффузии примесей или окисления. Большая часть моделей позволяет анализировать трехмерные структуры практически любой топологии.
Сквозное моделирование – от технологической последовательности изготовления структур до их схемотехнических моделей – подразделяется на несколько этапов. Набор данных, который получен после выполнения очередного этапа, используется в качестве входных данных для последующего моделирования. Выбор этапов (последовательности моделирования) в значительной степени определяется пользователем. Возможно автономное моделирование только отдельных процессов или характеристик, а также моделирование, начинающееся с практически произвольного этапа. В этом случае соответствующий набор входных параметров должен задаваться пользователем.
Пользователь, естественно, должен хорошо представлять границы применимости и возможности той или иной модели для того, чтобы обеспечить адекватное с физической точки зрения и приемлемое по точности и затратам времени решение задачи. С математической точки зрения значительная часть моделей физических процессов сформулирована в виде систем нелинейных интегро-дифференциальных уравнений.
Вычислительные процедуры адаптированы применительно к конкретной модели и выбираются автоматически. Тем не менее, важно понимать, что для решения большинства задач используются различные варианты методов последовательных приближений. Необходимая для реализации вычислений дискретизация обеспечивается использованием одно- двух- или трехмерных пространственных сеток, согласованных с топологией структуры. Выбор параметров сетки осуществляется пользователем. Неудачный выбор сетки в некоторых случаях не обеспечит приемлемой сходимости вычислительного процесса или точности вычислений, в отдельных случаях полученное решение может оказаться физически неадекватным. Чрезмерное усложнение сетки существенно увеличивает затраты времени на моделирование.
Одним из наиболее ответственных этапов подготовки к моделированию является создание одного или нескольких командных файлов. Структура этих файлов достаточно проста. Используется интуитивно понятный язык программирования. Файлы являются текстовыми и могут готовиться на любом ПК.
Командный файл отражает последовательность моделирования. С формальной точки зрения почти все команды задаются в виде неявных функций, каждая из которых определяет какой-либо этап моделирования. Набор параметров, естественно, индивидуален для каждой функции. Параметрами могут быть, например, виды примесей, режимы выполнения операций или режимы работы структуры. В наборе параметров часто указывается и подлежащая использованию модель процесса или явления, причем здесь, как уже отмечалось, могут использоваться и ссылки на пользовательские варианты программ моделирования тех или иных процессов. Указывается и набор выходных данных, хотя часто они определены по умолчанию. Наборы входных параметров каждой команды могут быть представлены аналитическими зависимостями с указанием интервалов варьирования их параметров, а также в форме численных массивов. Результаты моделирования представляются в виде массивов данных, которые могут быть отображены графически.
Пакет имеет мощный и гибкий пользовательский интерфейс, позволяющий визуализировать отдельные шаги процесса моделирования. Можно задать вывод данных для визуализации после выполнения нескольких итераций, по окончании выполнения той или иной команды, вид отображаемой информации (например, график, вид структуры с профилями распределения примесей, ВАХ и т.д.).
Метод конечных элементов.
Решение дифференциальных или интегро-дифференциальных уравнений с частными производными выполняется численными методами. Эти методы основаны на дискретизации независимых переменных — их представлении конечным множеством значений в выбранных узловых точках исследуемого пространства. Эти точки рассматриваются как узлы некоторой сетки, поэтому используемые методы — это сеточные методы.
Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей (МКР) и метод конечных элементов (МКЭ).
Основная идея метода конечных элементов состоит в том, что любую непрерывную область можно заменить моделью, состоящей из отдельных элементов (участков). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента.
В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что известны числовые значения этой величины в некоторых внутренних точках области (эти точки называют узлами). После этого можно перейти к общему случаю.
Чаще всего при построении дискретной модели непрерывной величины поступают следующим образом:
Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области;
В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами;
Значение непрерывной величины в каждой узловой точке первоначально считается известным, однако необходимо помнить, что эти значения в действительности еще предстоит определить путем наложения на них дополнительных ограничений в зависимости от физической сущности задачи;
Используя значения исследуемой непрерывной величины в узловых точках и ту или иную аппроксимирующую функцию, определяют значение исследуемой величины внутри области.
Решение задачи с применением МКЭ состоит из следующих основных этапов:
идентификация задачи, присвоение ей имени;
создание геометрии модели, пригодной для МКЭ;
разбиение модели на сетку конечных элементов;
приложение к модели граничных условий;
численное решение системы уравнений;
анализ результатов.
Построение сетки конечных элементов
Одним из наиболее важных этапов в конечно-элементном анализе является построение на модели сетки из конечных элементов, т. е. разделение всей модели на маленькие кусочки (конечные элементы), связанные между собой в узлах (рис. 1).
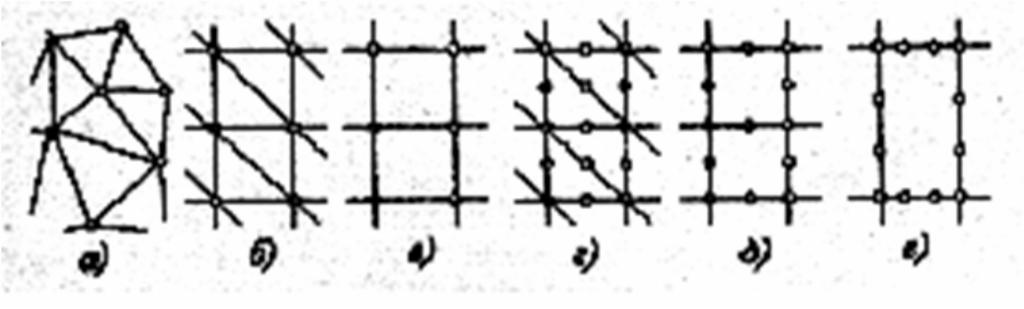
Рис. 1. Плоские конечные элементы: а) произвольная сетка; б) упорядоченная сетка треугольных элементов первого порядка; в) упорядоченная сетка прямоугольных элементов первого порядка; г, д) упорядоченная сетка элементов второго порядка; е) упорядоченная сетка элементов третьего порядка.
Произвольная сетка строится автоматически, при этом соседние элементы могут существенно отличаться по размерам. Упорядоченная сетка строится путем деления геометрических элементов модели на некоторое число частей, задаваемых пользователем. При этом форма элементов выбирается таким образом, чтобы сетка конечных элементов наилучшим образом воспроизводила геометрию моделируемого устройства. Размер элементов может быть довольно большим в однородных по составу и физическим параметрам частях модели, однако в области больших градиентов концентрации дефектов, легирующих примесей, полей физических величин, вблизи интерфейсов размер элементов должен быть достаточно маленьким, чтобы в расчете с достаточной точностью учитывались все изменения параметров при переходе между узлами сетки.
Очевидно, что чем меньше линейный размер конечного элемента, тем большее количество элементов в модели, при этом время вычислений экспоненциально возрастает, а ошибки анализа уменьшаются. Однако ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ.
Необходимо помнить, что МКЭ — приближенный метод, точность которого зависит от правильного выбора типов и размеров конечных элементов.
Лекция 2. Математические модели технологических процессов.
На микроуровне типичные математические модели представлены дифференциальными уравнениями в частных производных вместе с краевыми условиями. К этим моделям, относятся многие уравнения математической физики. Объектами исследования здесь являются поля физических величин, что требуется при исследовании процессов в твердых, жидких и газообразных средах, моделировании концентраций и потоков частиц в электронных приборах и т. п.
Количество совместно исследуемых различных сред (структурных элементов, слоев материала, фаз агрегатного состояния) в практически используемых моделях микроуровня не может быть большим ввиду сложностей вычислительного характера. Резко снизить вычислительные затраты в многокомпонентных средах можно, только применив иной подход к моделированию, основанный на принятии определенных допущений.
Допущение, выражаемое дискретизацией пространства, позволяет перейти к моделям макроуровня. Моделями макроуровня, называемыми также сосредоточенными, являются системы алгебраических и обыкновенных дифференциальных уравнений, в которых независимой переменной является только время t. Упрощение описания отдельных компонентов позволяет исследовать модели процессов в отдельных элементах, приборах, механических узлах, число компонентов в которых может доходить до нескольких тысяч.
В тех случаях, когда число компонентов в исследуемой системе превышает некоторый порог, сложность модели системы на макроуровне вновь становится чрезмерной. Поэтому, принимая соответствующие допущения, переходят на функционально-логический уровень. На этом уровне используют аппарат передаточных функций для исследования аналоговых (непрерывных) процессов или аппарат математической логики и конечных автоматов, если объектом исследования является дискретный процесс, т. е. процесс с дискретным множеством состояний.
Характерными примерами моделей микроуровня могут служить уравнения математической физики вместе с заданными краевыми условиями. Например, в физике полупроводниковых приборов используются:
Уравнения непрерывности:
для дырок:
![]()

и для электронов:
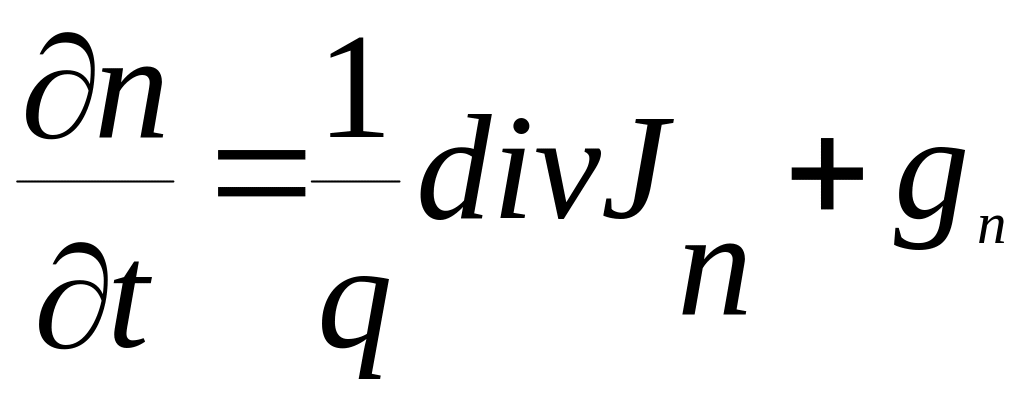 .
.
Уравнение Пуассона:
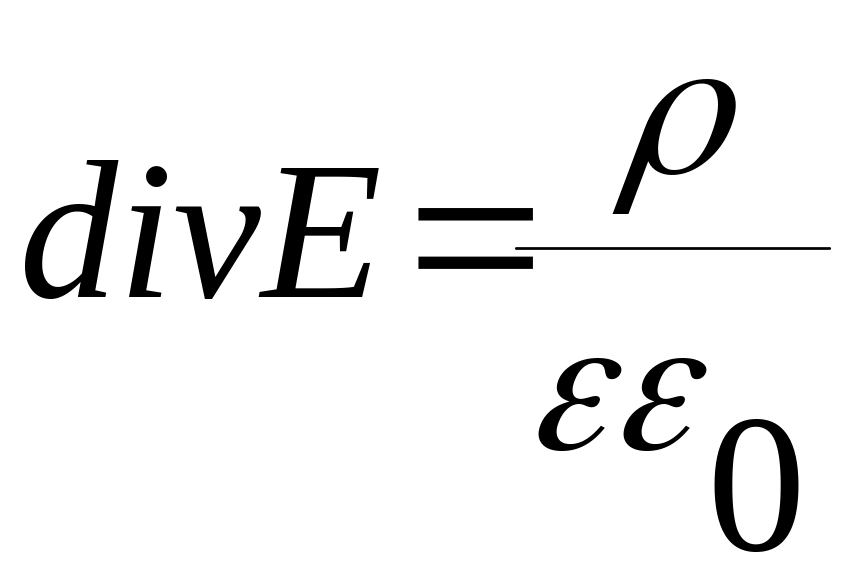 .
.
Здесь р и n — концентрации дырок и электронов; q — заряд электрона; Jp и Jn — плотности дырочного и электронного токов; gp и gn — скорости процессов генерации-рекомбинации дырок и электронов; Е — напряженность электрического поля; ρ — плотность электрического заряда; ε и ε0 — диэлектрическая проницаемость и диэлектрическая постоянная.
Краевые условия включают в себя начальные условия, характеризующие пространственное распределение зависимых переменных в начальный момент времени, и граничные, задающие значения этих переменных на границах рассматриваемой области в функции времени.
При моделировании технологических процессов в программном пакете Sentaurus TCAD используются различные модели процессов диффузии, имплантации и окисления. Выбор модели определяется условиями протекания процесса и возможностью пренебрегать влиянием определенных факторов (например, эффекта каналирования в процессе ионной имплантации или концентрационной зависимости коэффициента диффузии) на результат процесса. Основные из применяемых моделей перечислены ниже.
Модели диффузии
Основное уравнение для процесса диффузии:
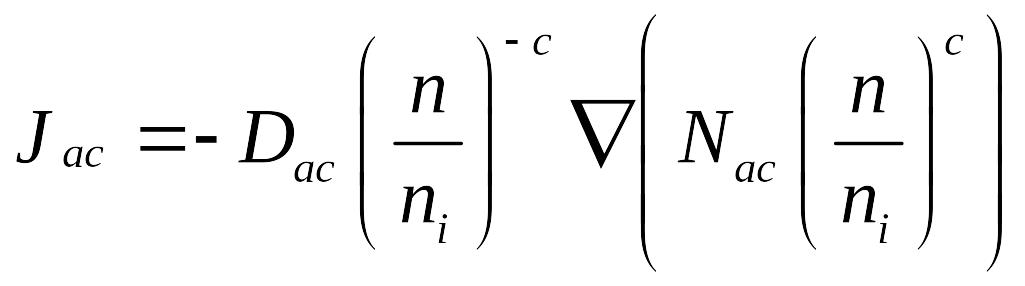 ,
,
где Jac - поток диффундирующих частиц,
a – тип примеси,
с – зарядовое состояние,
D – коэффициент диффузии,
N – концентрация примеси,
n – концентрация электронов.
Уравнение непрерывности для примеси типа a в зарядовом состоянии c
![]() ,
,
где
![]() -
вклад генерации – рекомбинации, связанный
с моделью переноса,
-
вклад генерации – рекомбинации, связанный
с моделью переноса,
![]() -
вклад генерации – рекомбинации, связанный
с процессом кластеризации.
-
вклад генерации – рекомбинации, связанный
с процессом кластеризации.
Sentaurus Process имеет 7 уровней моделей диффузии, различающихся по сложности. Наиболее полный вариант модели диффузии учитывает, что:
В процессе диффузии участвуют не только атомы примеси, но и дефекты кристаллической решетки, которые также диффундируют вместе с примесью в составе связанных комплексов.
И атомы примеси, и дефекты могут находиться в различных зарядовых состояниях.
Учитываются реакции ионизации, как атомов примеси, так и дефектов, ионизация связанных комплексов.
Учитывается взаимодействие дефектов между собой, а также связанных комплексов с дефектами противоположного типа.
Уравнения, описывающие все вышеперечисленные процессы, должны быть включены в полную модель диффузионного процесса наряду с уравнением диффузии и уравнением непрерывности.
Моделирование процесса диффузии с участием одной примеси
Примем следующие обозначения: A – атом примеси, находящийся в узле решетки, (замещающий атом), B - атом примеси, находящийся в междоузлии, V – вакансия, I – междоузлие, i, j, k, l – зарядовые состояния, причем будем считать, что i, j, k, l = 0, ± 1, ± 2.
Тогда основные реакции, которые учитываются в модели связанной диффузии, запишутся следующим образом (12 уравнений):
- образование/распад пар дефект–примесь с высвобождением/связыванием электронов:
1) Ai + Ij ↔ (AI)i+k + (k - j)n;
2) Ai + Vj ↔ (AV)i+k + (k - j)n;
- генерация-рекомбинация Френкелевских пар с захватом или высвобождением электронов:
3) Ii + Vj ↔ - (i + j)n;
-взаимодействие пар дефект–примесь с дефектом противоположного типа:
4) (AI)i+j + Vk ↔ Ai - (j + k)n;
5) (AV)i+j + Ik ↔ Ai - (j + k)n;
- взаимодействие пар дефект–примесь противоположного типа:
6) (AI)i+j + (AV)l+k ↔ Ai + Al - (j + k)n;
- ионизация пар:
7) (AI)i+j ↔ (AI)i+k + (k - j)n;
8) (AV)i+j ↔ (AV)i+k + (k - j)n;
- ионизация дефектов:
9) Ij ↔ Ik + (k - j)n;
10) Vj ↔ Vk + (k - j)n;
- эстафетный механизм:
11) Ai + Ij ↔ Bk + (k – i - j)n;
- реакция Франка–Торнбула:
12) Ai ↔ Bk + Vj + (k – i + j)n.
Кинетика протекания реакции
Реакции, используемые при моделировании, можно представить в общем виде:
aA+ bB ↔ pP+ qQ;
стехеометрические коэффициенты в этом уравнении a, b, p, q – положительные и, как правило, целые, A, B, P, Q – концентрации.
Кинетика протекания реакции описывается уравнением:
R = kF(AaBb – kRPpQq),
где kF – скорость прямой реакции, kR - скорость обратной реакции.
При kF → ∞ (быстрое протекание прямой реакции) получаем алгебраическое соотношение:
AaBb – kRPpQq = 0.
В противном случае (при конечном значении kF) реакция рассматривается как неравновесная.
Каждое из 12 рассмотренных уравнений должно быть дополнено кинетическим уравнением. Например, для уравнений образования/распада пар дефект–примесь можно записать:
1) Ai + Ij ↔ (AI)i+k + (k - j)n,
R1ijk = kF(AiIj – kR(AI)i + k [n/ni]k – j).
Кинетическое уравнение для пар вакансия-примесь:
2) Ai + V j ↔ (AV)i+k + (k - j)n,
R1ijk = kF(AiVj – kR(AV)i + k [n/ni]k – j).
Одним из наиболее общих допущений является предположение, что реакции ионизации всегда являются равновесными. Отсюда следует, что для реакций ионизации пар (уравнения 7-8) и ионизации дефектов (уравнения 9-10):
R7 = R8 = R9 = R10 = 0
Для составления модели необходимо записать уравнение непрерывности для каждой составляющей процесса диффузии, а именно:
1) атомов примеси в узлах и междоузлиях Ai , Bk;
2) дефектов – междоузлий и вакансий Ii , Vj;
3) комплексов примесь – дефект (AI)i+j, (AV)l+k.
Уравнения должны быть составлены для каждого зарядового состояния отдельно.
Уравнения непрерывности составляются с учетом протекающих реакций:
∂N/∂t + divJ = ∑RN,
где RN – кинетические составляющие для всех реакций, протекающих с участием элемента N.
Например, составим уравнение непрерывности для междоузлий, находящихся в зарядовом состоянии j.
Междоузлия участвуют в процессах:
- образование/распад пар дефект–примесь (уравнение 1);
- генерация-рекомбинация Френкелевских пар (уравнение 3);
- взаимодействие пар дефект–примесь с дефектом противоположного типа (уравнение 5);
- ионизация дефектов (уравнение 9);
- эстафетный механизм (уравнение 11).
Учитывая, что реакция ионизации дефектов относится к равновесным реакциям, в правой части уравнения непрерывности для Ij останется четыре типа генерационно- рекомбинационных составляющих:
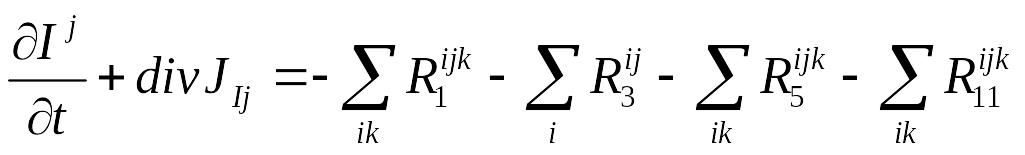 .
.
В модель необходимо включить также уравнение диффузии для каждой составляющей диффузионного процесса.
Также необходимо добавить уравнение Пуассона для всех заряженных частиц, участвующих в процессе: заряженных дефектов, заряженных атомов примеси в двух состояниях (замещающем и междоузельном) и заряженных пар дефект – примесь.
Если в процессе участвуют две или более примеси, то количество уравнений еще увеличивается.
Упростить моделирование можно, если учесть тот факт, что примесь, как правило, находится в одном зарядовом состоянии, и не все возможные пары дефект–примесь образуются в реальности. Кроме того, вклад некоторых пар в диффузию незначителен.
Модели процессов ионной имплантации и высокотемпературного отжига
При моделировании процессов ионной имплантации используются следующие аналитические аппроксимации распределения ионов: функция Гаусса, двойное сопряженное распределение Гаусса (асимметричное), распределение Гаусса с обобщенным экспоненциальным «хвостом», распределение Пирсона-IV, распределение Пирсона -IV с линейно-экспоненциальным хвостом. Функции распределения характеризуются моментами:
средний проективный пробег: RP = μ1 =
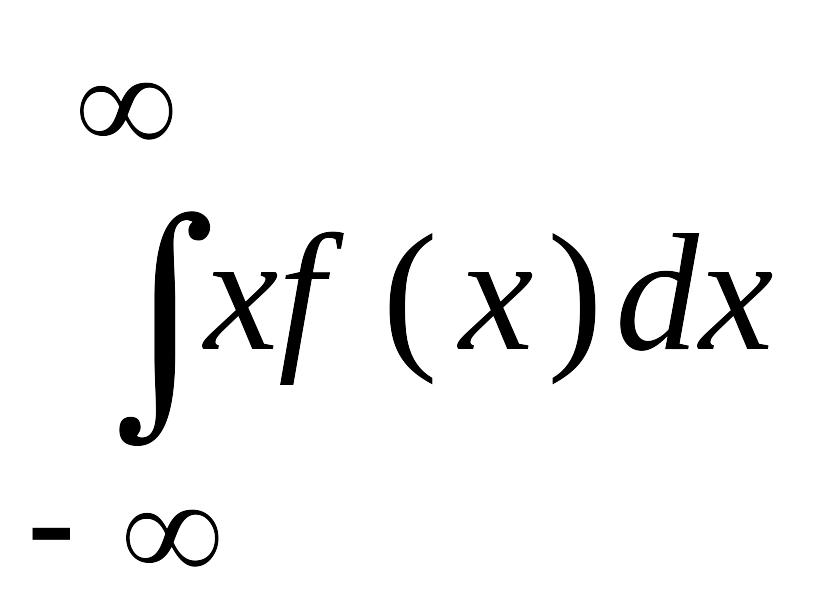 ,
,моменты более высокого порядка: i=2, 3, 4:
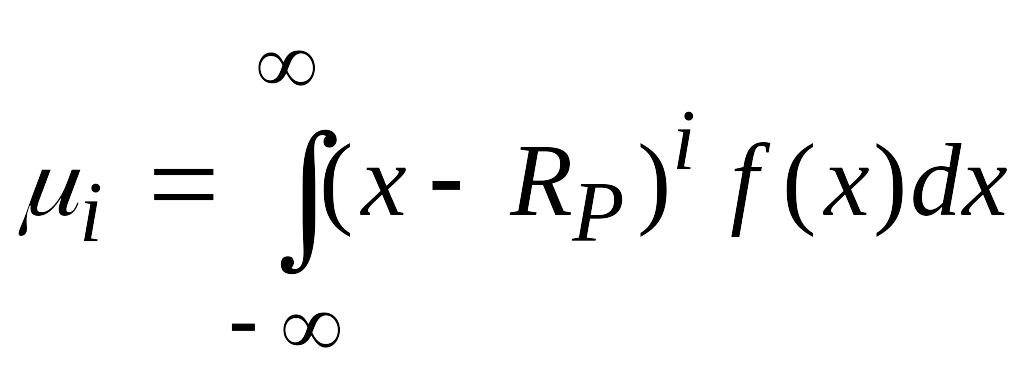 ,
,среднеквадратичное отклонение: σP = (μ2)1/2,
асимметрия:
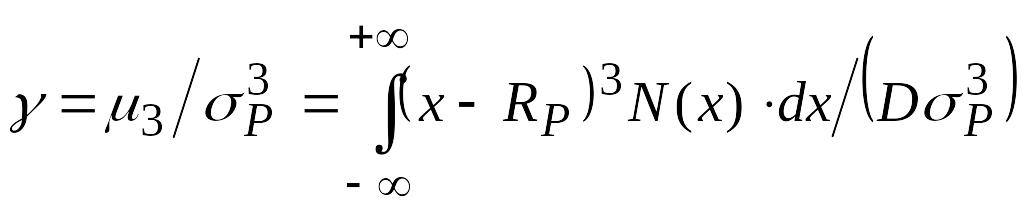 ,
,эксцесс, характеризует плавность вблизи вершины:
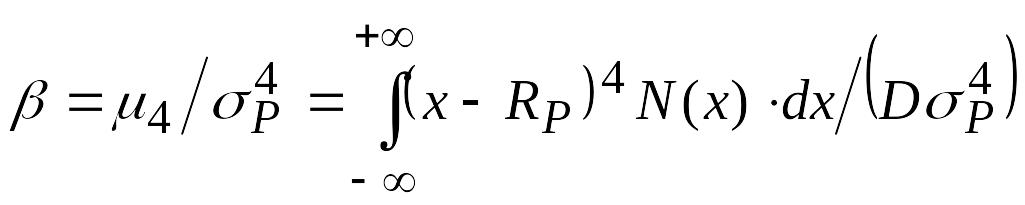 .
.
Функция Гаусса
В соответствии с классической теорией ЛШШ и диффузионной моделью Бирсака профили имплантированных ионов должны описываться гауссовым распределением. Аппроксимация распределения ионов по нормальному закону - распределение Гаусса является симметричным распределением и характеризуется двумя параметрами Rp и σp:
N(x)
=
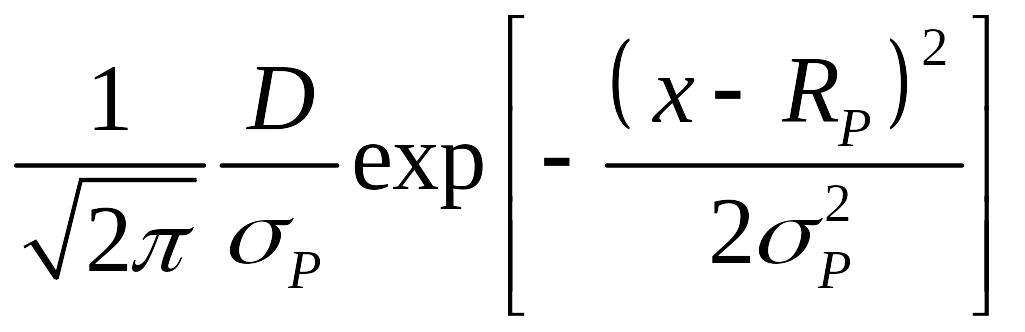 ,
,
где D – доза имплантированной примеси, см-2, Rp, σp - средняя проекция пробега ионов и среднеквадратичное отклонение проекции пробега.
Двойное сопряженное распределение Гаусса (асимметричное)
N
(x)
=
 ,
,
![]() =
=
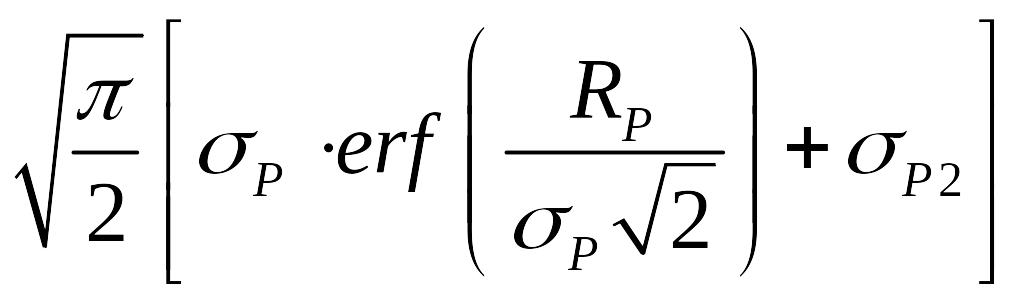 ≈
≈
![]() ,
,
![]() -
функция ошибок.
-
функция ошибок.
Распределение Гаусса с обобщенным экспоненциальным «хвостом»
N(x)
=
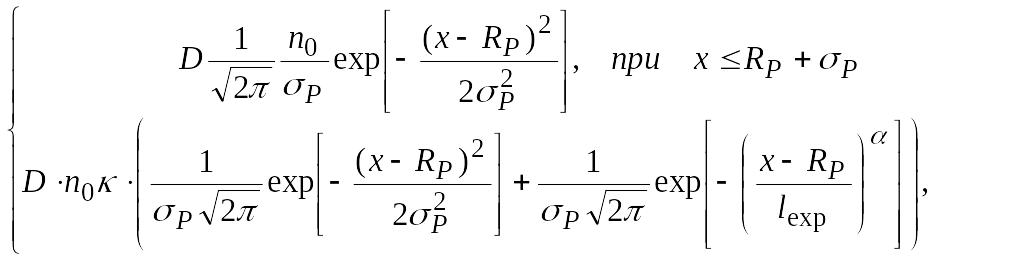
Распределение Пирсона-IV
Решение дифференциального уравнения,
![]() ,
где z
= x
– Rp:
,
где z
= x
– Rp:
N(x)
=
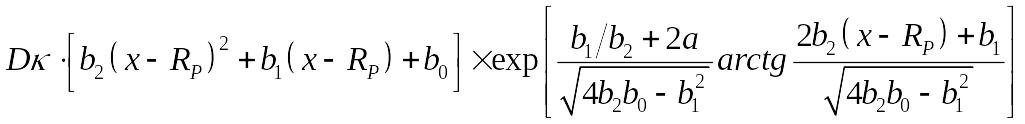 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Распределение Пирсона -IV с линейно- экспоненциальным хвостом
N(x)
=
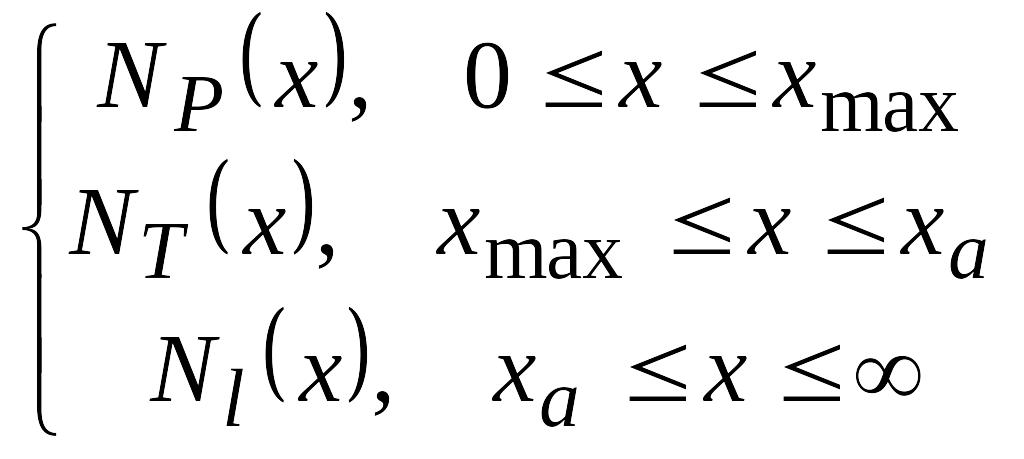 ,
,
где xmax - координата максимума функции распределения Пирсона.
![]() ,
,
Np(x) - распределение Пирсона –IV,
![]() ,
,
![]() -
функция распределения в переходной
области,
-
функция распределения в переходной
области,
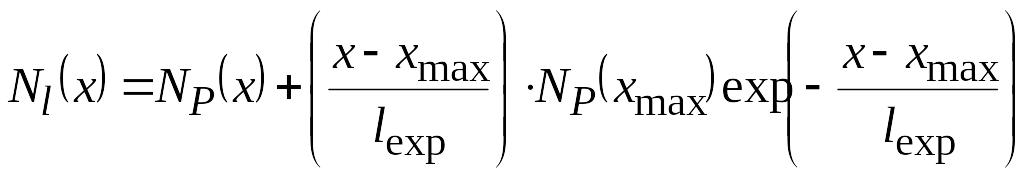 ,
,
![]() -
функция распределения в "хвостовой
части".
-
функция распределения в "хвостовой
части".
Моделирование операции окисления
При росте слоя окисла происходят следующие процессы:
- растворение окислителя на границе газ-окисел;
- перенос окислителя через растущий окисел;
- поглощение окислителя на границе кремний – окисел;
- перемещение границ слоев;
- механические напряжения, связанные с ростом окисла и изменением объема.
Растворение и поглощение моделируется через задание граничных условий, перенос окислителя рассчитывается как диффузионный процесс.
Диффузия окислителя подчиняется закону Фика:
![]()
![]()
где J – поток окислителя, С – концентрация окислителя, D – коэффициент диффузии окислителя.
Условие на границе газ–окисел:
![]()
где h – коэффициент массопереноса, С* - растворимость окислителя, зависящая от давления и температуры.
Условие на границе кремний – окисел:
J = βkCSi,
где β – стехеометрический коэффициент (β = 1 для кислорода, β = 2 для паров воды), k – скорость химической реакции, CSi – плотность частиц кремния на границе раздела кремний–окисел.
Скорость химической реакции и коэффициент диффузии вычисляются из линейной и параболической констант, используемых в модели Дила–Гроува, которая иллюстрируется схемой, приведенной на рис. 2.
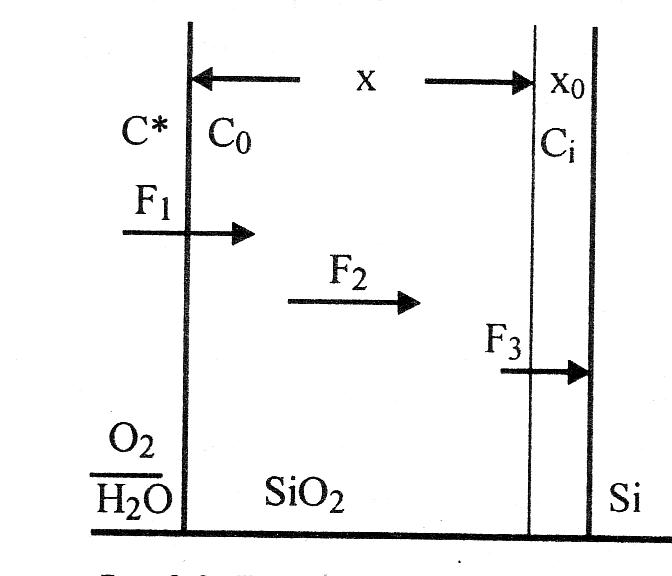
Рис. 2. Модель Дила-Гроува.
F1 = h(C*-C0) – массоперенос через внешнюю границу окисла, C*, C0 – концентрации окисляющих частиц;
F2 = D(C0 – Ci)/x – диффузия окислителя через окисел к границе раздела окисел/кремний;
F3 = kCi – химическая реакция на границе раздела окисел/кремний.
В условиях равновесия F1 = F2 = F3:
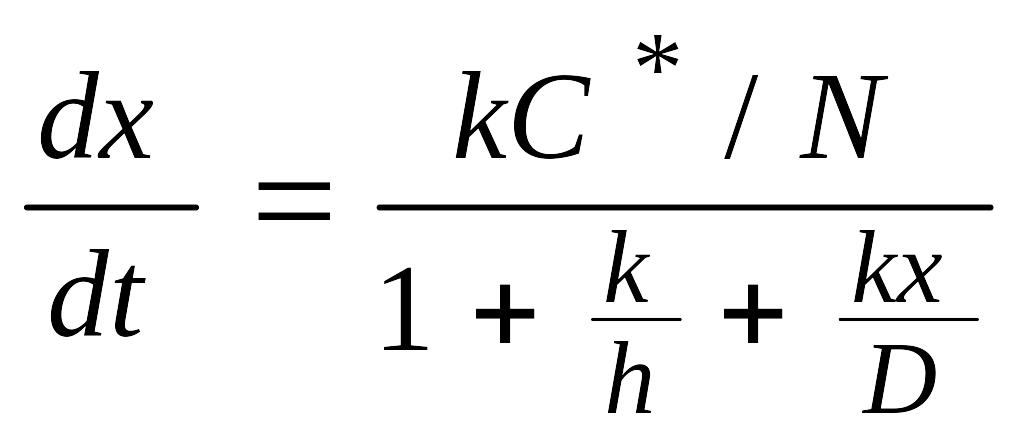 .
.
Обозначив B = 2DC*/N, получаем:
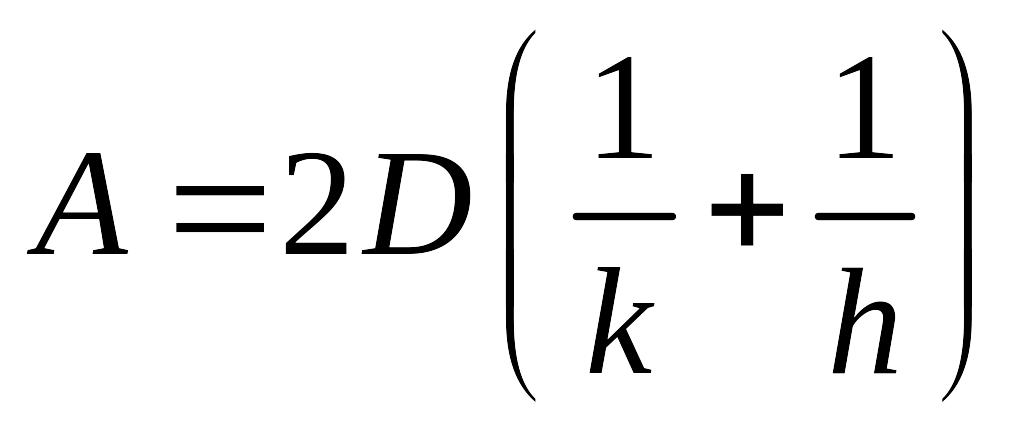 ,
, ![]() .
.
Связь с коэффициентами B и B/A:
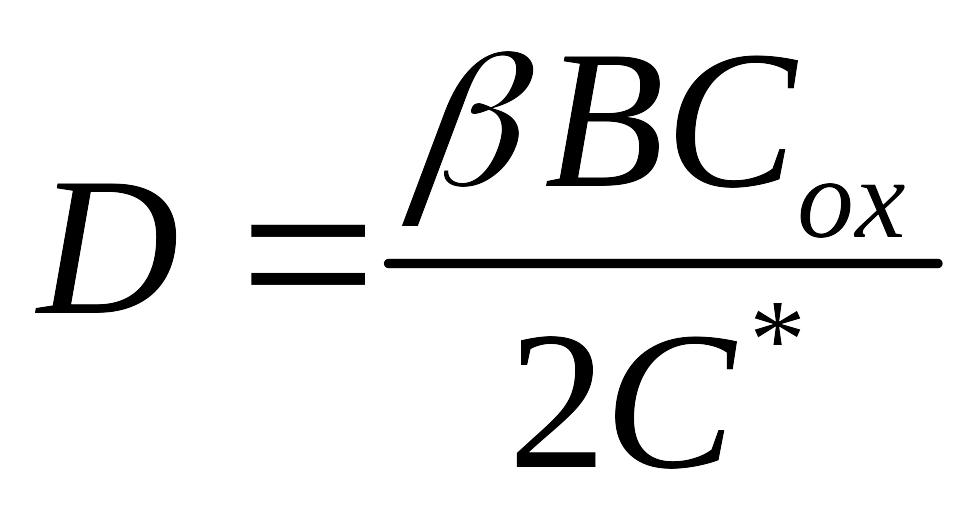 ,
, 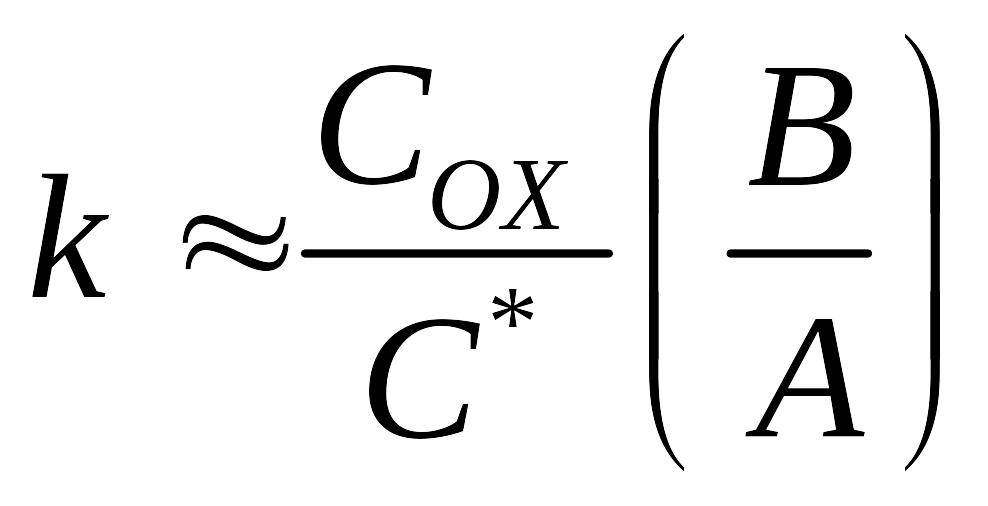 ,
,
где СOX – плотность частиц окисла.
Константа параболического роста B и константа линейного роста B/A зависят от температуры по закону Аррениуса. Значения констант в программе Sentaurus Process определяются через заданные значения коэффициентов и энергий активации в температурной зависимости. Константа В зависит от парциального давления окислителя.
При моделировании окисления также учитываются:
- зависимость от ориентации;
- зависимость от механических напряжений;
- зависимость от уровня легирования.
Выражения для расчета констант параболического и линейного роста в среде сухого и влажного кислорода приводятся ниже:
![]() ,
, 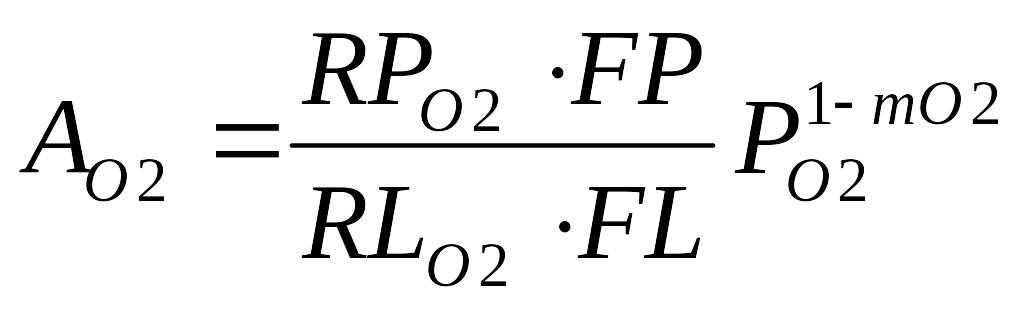 ,
,
![]() ,
,
B = BO2 + BH2O,
ВО2 = FP∙RPO2∙pO2,
ВH2О = FP∙RPH2O∙pH2O,
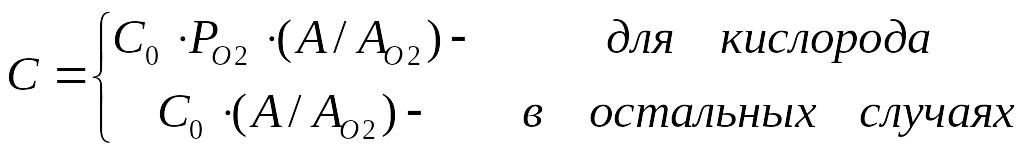
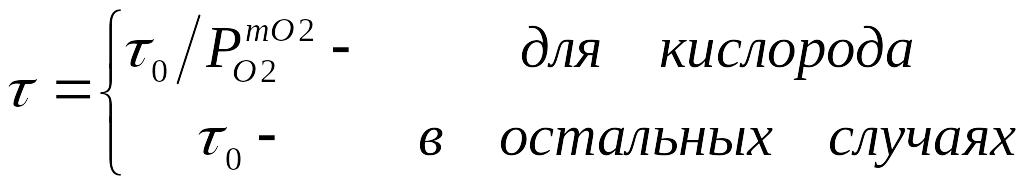
RP и RL – константы параболического и линейного роста,
FP и FL – коэффициенты ускорения окисления в сильнолегированных слоях.
Модель Массуда для начального этапа процесса окисления
![]()
Параметры C и L зависят от кристаллографической ориентации и температуры.
Двумерное моделирование процесса окисления
Очень часто требуется провести моделирование окисления рельефной поверхности или окисления отдельного участка подложки, не защищенного маской (локальное окисление). В качестве маски при окислении используется нитрид кремния Si3N4, коэффициент диффузии кислорода в котором очень мал. В подобных случаях окисление является существенно неодномерным.
Составляющие численных моделей неодномерного роста окисла:
исходная модель одномерного окисления (Массуда или Дила-Гроува);
учет вязкоупругих свойств материалов;
моделирование перемещения межфазной границы в пространстве;
решение уравнения диффузии в присутствии движущихся границ.
Учет вязкоупругих свойств материалов. Вязкая модель.
При температурах окисления выше 950 °С окисел можно рассматривать как вязкую жидкость. Тогда движение его границ определяется процессом вязкого течения согласно уравнению:
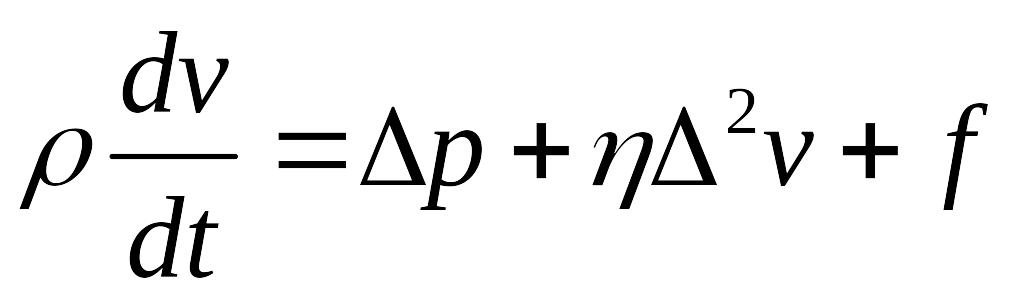
где ρ, η - плотность и вязкость стекла, v – скорость движения элементов, p – давление, f – гравитационная сила.
Большая вязкость и относительно малая скорость роста (v < 1 нм/с) позволяют пренебречь в этом уравнении гравитационным и ускоряющим членами. Тогда имеем уравнение Навье – Стокса, где вязкая сила уравновешивается градиентом давления:
![]() .
.
Если окисел можно считать несжимаемой жидкостью, то уравнение непрерывности потока для вязкого течения несжимаемой жидкости имеет вид Δη = 0.
Вязкоупругая модель.
Если принимать во внимание упругопластичные свойства окисла и рассматривать его при температуре окисления как сжимаемую жидкость, то необходимо учитывать уравнение, описывающее соотношение между давлением и плотностью, а также рассчитывать механические напряжения в структуре. В линейной вязкоупругой модели принимается линейная зависимость между механическим напряжением и тензором деформаций в окисле.
В присутствии механических напряжений константа скорости реакции окисления и коэффициент диффузии окислителя уменьшаются, это необходимо учесть при решении задачи с учетом механических напряжений.
Решение уравнения диффузии в присутствии движущихся границ.
Если границы раздела неподвижны, то процесс диффузии описывается первым и вторым законом Фика:
![]() ,
, ![]() ,
,
где Z – зарядовое состояние иона примеси, μ – подвижность примеси, NI – концентрация электрически активной примеси, E – напряженность электрического поля.
Пусть
![]() - скорость движения границы, тогда
уравнение непрерывности будет иметь
вид:
- скорость движения границы, тогда
уравнение непрерывности будет иметь
вид:
![]() .
.
Из
уравнения непрерывности при условии
![]() получаем:
получаем:
![]() .
.
Диффузионный поток заменяется суммой диффузионного потока и конвективного потока. При окислении и силицидизации конвективный поток может доминировать.
Учет перераспределения примеси в структуре в процессе окисления.
Процесс окисления является высокотемпературным процессом, поэтому необходимо моделировать перераспределение примеси в структуре. Диффузия примесей в окислительной атмосфере моделируется с учетом двух факторов:
1) изменение скорости (ускорение или замедление) процесса диффузии в присутствии окислительной атмосферы;
2) сегрегация примеси на границе раздела кремний–окисел.
Сегрегация примеси.
Равновесный коэффициент сегрегации – это отношение равновесных растворимостей примеси при данной температуре в кремнии и окисле:
![]() .
.
Для бора m0 = 0.1 – 0.3 (бор поглощается окислом); для донорных примесей m0 > 10 (донорная примесь выталкивается из окисла в кремний).
Во время роста окисла нарушается равновесное соотношение концентраций, определяемое выражением:
![]() ,
,
![]() -
концентрация примеси вблизи границы
раздела.
-
концентрация примеси вблизи границы
раздела.
Появляется сегрегационный поток примеси JS:
![]() ,
,
где λS - константа скорости химической реакции сегрегации, b = 0.44 – коэффициент поглощения кремния окислом, vOX – скорость роста окисла.
Эффективный коэффициент сегрегации в процессе роста окисла, считая, что поток примеси в окисле пренебрежимо мал:
![]()
При моделировании процессов диффузии в Sentaurus Process могут быть заданы граничные условия шести типов:
HomNeumann,
Natural,
Dirichlet,
Segregation,
ThreePhaseSegregation,
EpiTransfer.
А также специальные граничные условия на движущихся границах раздела.
HomNeumann:
- предполагается, что потоки через границу равны нулю;
- устанавливается по умолчанию на левой, правой, и нижней границах.
Natural:
![]()
h – скорость поверхностной рекомбинации, С и С* - концентрация и равновесная концентрация, соответственно.
- задается по умолчанию для точечных дефектов (вакансий и междоузлий) на границах газ–кремний и окисел–кремний.
Dirichlet:
- значение концентрации на границе считается равным задаваемому равновесному значению.
Segregation:
- устанавливается по умолчанию для всех примесей:
![]()
![]() -
концентрации
примеси с одной и другой стороны от
границы раздела, h
– скорость переноса через границу, s
– скорость сегрегации для примеси A.
-
концентрации
примеси с одной и другой стороны от
границы раздела, h
– скорость переноса через границу, s
– скорость сегрегации для примеси A.
ThreePhaseSegregation:
- более сложная модель на границе раздела;
- позволяет учесть важный эффект потери дозы;
- при сегрегации часть примеси накапливается на границе раздела, становясь неактивной.
EpiTransfer:
- специальное условие для процесса эпитаксии;
- позволяет задать резкий скачок на границе раздела между подложкой и эпитаксиальным слоем.
![]() ,
,
Transfer – скорость переноса.
Лекция 3. Программный пакет Sentaurus TCAD. Модуль Sentaurus Process.
Sentaurus Process (sprocess) – это программа многомерного моделирования процессов производства приборов на основе кремния и сложных полупроводников. Данный блок программы представляет собой симулятор для расчета 1D, 2D и 3D процессов. Sentaurus Process моделирует все известные технологические процессы, такие как диффузия, имплантация, окисление, травление, нанесение слоев. Использование sprocess специального языка Alagator позволяет пользователю решать его собственные уравнения диффузии. Язык программирования Alagator может быть использован для решения любых уравнений диффузии, с учетом влияния дефектов, концентрации ранее введенной примеси и окисления.
Sentaurus Process имеет уникальные возможности моделирования современных кремниевых и некремниевых технологий благодаря обширной библиотеке последних экспериментальных данных и использованию проверенной методологии калибровки.
Типы файлов, используемые в SProcess:
Командный файл: *.cmd;
Описание процесса выполнения командного файла, используемых моделей и значения величин физических параметров: *.log;
Файл, содержащий описания структуры и набора данных: без расширения;
Геометрия прибора: *_bnd.tdr;
Геометрия, сетка и набор данных (например, профили легирования): _fps.tdr, _fps.grd, _fps.dat;
Профили распределения примесей или другие данные, на основании которых можно построить двухкоординатные графики: *.plx.
Начало работы с SProcess
Чтобы приступить к вводу команд и построчному исполнению программы в окне Терминала наберите команду: sprocess и нажмите Enter;
Чтобы выполнить командный файл в окне Терминала наберите команду: sprocess file_name.cmd и нажмите Enter.
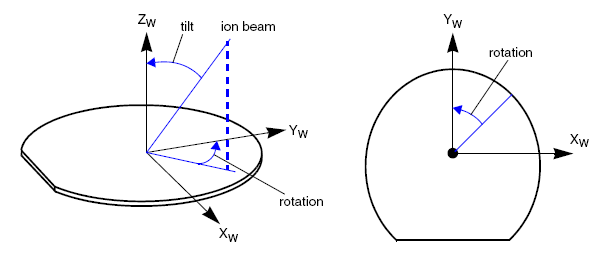
Система координат, в которой строится модель в Sentaurus Process, не совпадает с системой координат, связанной с подложкой (см. рис. ). В Sentaurus Process система координат служит для задания сетки конечных элементов. Ось x в системе координат Sentaurus Process направлена вглубь подложки, а ось y ориентирована вдоль базового среза. При построении одномерных моделей используется только ось x, для 2D моделей – оси x и y. Поворот осей системы координат Sentaurus Process относительно системы координат, связанной с подложкой задается параметром slice.angle в команде init. Угол поворота оси отмеряется от оси y системы координат, связанной с подложкой, до оси y системы координат, используемой в Sentaurus Process. Положительным считается направление поворота оси y относительно оси zw против часовой стрелки. По умолчанию устанавливается значение параметра slice.angle равное – 90°.

Создание сетки конечных элементов и определение области моделирования
При построении сетки необходимо соблюдать несколько правил:
- в случае, если моделируемая структура - не первая в открытом сеансе SProcess, необходимо использовать команду line clear, чтобы удалить созданную с помощью команды line сетку;
- значения параметра location в команде line должны задаваться в порядке возрастания;
- границы области моделирования задаются с помощью параметра tag в команде line;
- для описания подложки должна задаваться как минимум одна команда region;
- в команде region должно задаваться описание материала. Исключение составляет случай использования команды substrate, описание которой дано ниже;
- размерности структуры, описываемой с помощью команд region и line должны совпадать (например, если в команде line присутствует координата y, предполагается, что моделируемая структура – двумерный объект, для которого в команде region должны быть заданы параметры ylo и yhi);
- параметр spacing используется для построения линий сетки между линиям, определяемыми параметром location команды line. SProcess плавно изменяет расстояние между линиями сетки в соответствии со значениями, заданными пользователем с помощью параметра spacing. По умолчанию устанавливается слишком большое значение параметра spacing, так что сетка строится только из линий, определяемых параметром location.
- параметр *lo соответствует минимальному значению координаты описываемой области моделирования. Таким образом, метка xlo должна располагаться в точке с меньшим значением координаты x, чем метка xhi;
- шаг построения сетки в направлении y может быть задан достаточно большим. Так как, в основном, неоднородности типа интерфейсов между разнородными материалами или значительные градиенты параметров присутствуют вблизи поверхности структуры и в направлении оси x, увеличение размера ячеек сетки вдоль оси y позволяет получать решения с высокой точностью при сокращении расчетного времени;
- для построения более мелкой сетки в отдельной области структуры используется команда refinebox.
Пример описания области моделирования:
region silicon xlo=SubTop xhi=SubBottom ylo=SubLeft yhi=SubRight
Инициализация моделирования
Область моделирования задается с помощью команды init, в качестве параметров которой используются указание концентрации легирующей примеси (параметр concentration) или удельного сопротивления подложки (параметр resistivity) и наименование вещества примеси (параметр field).
Пример использования команды init:
init concentration=1e+15<cm-3> field=Boron
В качестве входных данных с помощью команды init могут быть загружены результаты предварительного расчета, например, сохраненные в файле формата tdr:
init tdr=filename, где filename – имя файла.
Описание процесса перестроения сетки
При моделировании процессов, приводящих к изменению геометрии прибора, например, нанесения и удаления слоев, чтобы находить значения физических параметров требуется в создаваемых областях строить сетку конечных элементов. Это выполняется процессором Mgoals, запускаемым с помощью команды mgoals on. Mgoals, по возможности, сохраняет неизменной существующую сетку, достраивает ее в соответствии с параметрами, которые заданы в команде mgoals on, в новых областях и уменьшает размер элементов сетки вблизи новых интерфейсов. Пример параметров этой команды:
mgoals on normal.growth.ratio=1.1 accuracy=2e-5\
min.normal.size=50<nm> max.lateral.size=6.0<um>
Параметр min.normal.size задает размер элементов первого (ближайшего к интерфейсу) ряда сетки в новой области. Параметр max.lateral.size определяет не только максимальный размер элементов в горизонтальном направлении вдоль структуры при двумерном моделировании, но и максимальный размер элемента в любом другом направлении. Параметр normal.growth.ratio задает коэффициент приращения размера элементов от слоя к слою. Параметр accuracy определяет, с какой точностью выполняется построение сетки на криволинейных участках структуры (единицы измерения - мкм).
Описание технологических процессов:
Осаждение
Имплантация
Значения углов tilt и rotation поясняет рис. Углы отмеряются по направлению от ионного пучка к соответствующей оси координат.
Высокотемпературный отжиг
Удаление
Запись результатов моделирования в файл
Сохранение результатов моделирования в файл выполняется с помощью команды struct. При этом имеется возможность сохранить полную информацию о геометрии, границах, сетке, легировании и результатах моделирования в один файл с расширением .tdr, или раздельно сохранить данные о геометрии и сетке в файл с расширением .grd, а данные об уровнях легирования и результатах расчета в файл с расширением .dat. Данные, сохраненные таким образом, можно просматривать с помощью модуля Tecplot_sv или загружать в качестве исходных данных для последующего моделирования.
Сохранение данных об одномерных профилях легирования выполняется с помощью команды Writeplx. Выбор данных, подлежащих сохранению выполняется с помощью команды SetPlxList. По умолчанию список записываемых данных пуст. Просмотр результатов, сохраненных в файле с расширением .plx, осуществляется с помощью программы Inspect.
Лекция 4. Программный пакет Sentaurus TCAD. Модули Ligament Layout Editor и Ligament Flow Editor.
Ligament обеспечивает удобный графический интерфейс для создания и редактирования процессов моделирования. Среда Ligament предназначена для настройки и выполнения моделирования в представлении более понятном пользователю. Входные командные файлы создаются автоматически при проектировании технологического процесса. Открытая и понятная пользователю архитектура позволяет наглядно увидеть все процессы получения прибора, а также вносить изменения и дополнения в технологический процесс.
Ligament Layout Editor используется для создания эскизов шаблонов для 3D и 2D моделирования. Для каждой операции литографии шаблон строится в отдельном «слое» с помощью простейших геометрических фигур. Полученные эскизы можно передавать для изготовления реальных шаблонов с помощью генератора изображений.
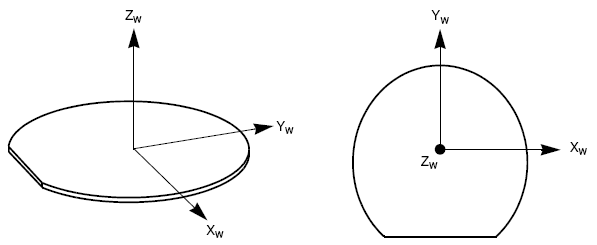
Система координат, в которой строится эскиз шаблона, связана с системой координат, привязанной к плоскости подложки таким образом, что ось x направлена вдоль базового среза, ось y – перпендикулярно ему в плоскости подложки, ось z – по нормали к поверхности подложки (см. рис. ). Базовый срез подложек с ориентацией (100) расположен вдоль направления <110>, у подложек с ориентацией (111) – вдоль направления <1-10>.
Чтобы запустить программу Ligament Layout Editor в окне Терминал наберите команду prolyt и нажмите Enter. Откроется рабочее окно программы с чистым листом для рисования масок. Также на экране появится диалоговое окно Layout Dimensions, в котором можно задать размер области рисования и шаг сетки. Рекомендуется определять шаг сетки, поскольку все операции рисования и перемещения объектов привязаны к узлам сетки.
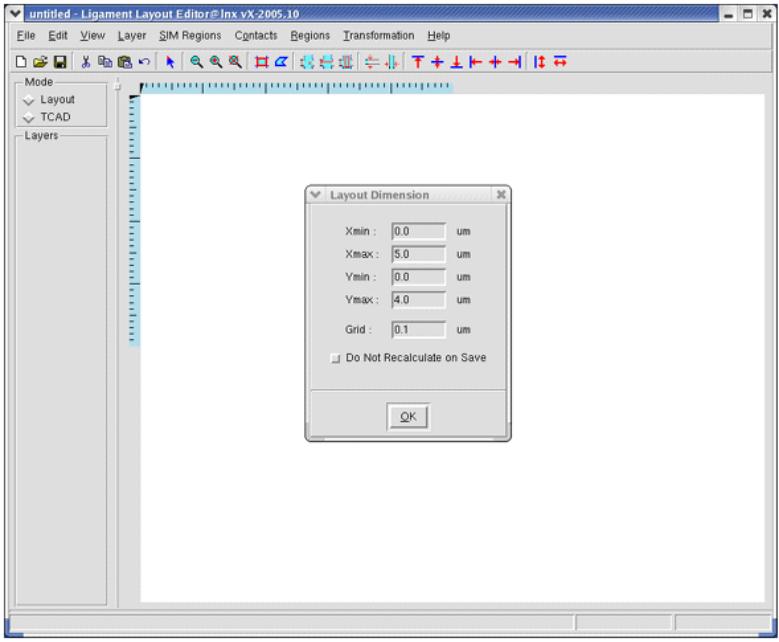
Рис. 1. Вид рабочего окна Ligament Layout Editor и диалогового окна Layout Dimensions.
В рабочем окне программы имеется несколько секторов:
- Область рисования, которая находится справа;
- Область Mode в левом верхнем углу предназначена для выбора режима работы. В режиме Layout выполняются основные операции рисования и редактирования рисунка шаблонов. В режиме TCAD пользователь получает доступ к специфическим функциям TCAD.
- Область Layout, расположенная ниже области Mode содержит список слоев, имеющихся в открытом файле. Пользователь имеет возможность в этом окне выбирать активный слой.
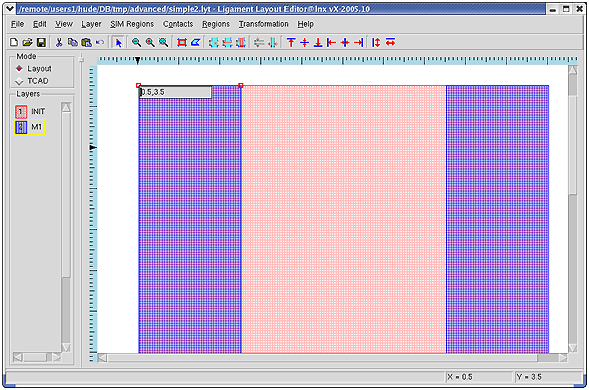
При построении эскизов шаблонов в Layout Editor рекомендуется сначала обозначить область рисования. С помощью диалогового окна Layout Dimensions задаются размеры области, за пределами которой курсор становится неактивным. Кроме того, рисуется нулевой слой INIT, чтобы сделать границы области рисования видимыми. Для этого:
- переключитесь в режим работы Layout;
- в списке слоев в качестве активного должен быть слой INIT;
- на панели инструментов нажмите иконку Add a new rectangle to the layer:
- нарисуйте прямоугольник. Для этого установите курсор в левом верхнем углу области рисования и протяните его (при нажатой левой клавише мыши) до правого нижнего угла области рисования. Координаты, соответствующие положению курсора, отображаются внизу окна Layout Editor в строке состояния.
Чтобы сохранить файл:
в меню File выберите Save Layout As>DF-ISE;
введите имя файла;
файлу автоматически будет присвоено расширение .lyt.
Рисование шаблонов включает следующие операции:
Добавление нового слоя. Для этого:
- в режиме Layout дважды кликните мышкой на названии слоя INIT. При этом откроется диалоговое окно Edit Layers.
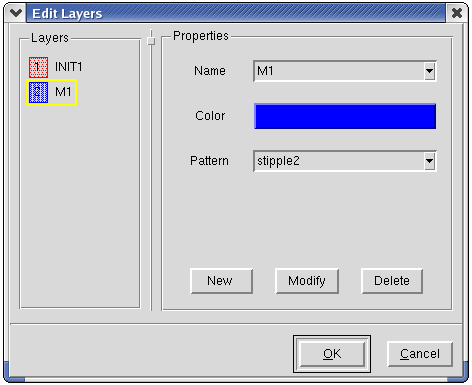
- в строке Name введите имя нового слоя, соответствующее имени маски в командном файле;
- измените цвет слоя;
- в строке Pattern выберите очередную метку (номер слоя);
- нажмите кнопку New. При этом новый слой добавится в список в окне Layers.
- нажмите OK.
2) Создание рисунка маски в новом слое:
- сделайте активным новый слой.
- нажмите иконку Add a new rectangle to the layer.
- прямоугольниками изобразите области, которые должны быть закрыты маской.
Чтобы увидеть или изменить координаты точки:
- слой, в который будут вноситься изменения, должен быть активным;
- дважды щелкните мышкой внутри прямоугольника, с вершинами которого вы намерены работать. При этом все вершины этого прямоугольника будут выделены;
- поместите курсор в положение нужного угла и дважды щелкните мышкой. При этом рядом с выбранной вершиной появится окошко с ее координатами;
- измените координаты и нажмите Enter.
Определение области моделирования.
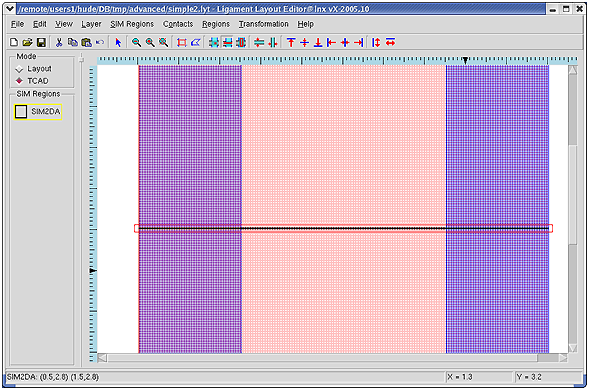
Область моделирования может быть определена в Ligament Layout Editor и передана в Ligament Flow Editor. 3D моделирование выполняется с использованием полной топологии, которую создают прямоугольные фигуры шаблона. Для проведения 2D моделирования на шаблоне проводится линия, обозначающая положение сечения в структуре. Для 1D моделирования на шаблоне выбирается точка, в которой строится модель по направлению, перпендикулярному к рисунку шаблона.
Чтобы выделить область для 2D моделирования:
- переключитесь в режим TCAD;
- нажмите иконку Select line for 2D simulation
- проведите линию, обозначающую область моделирования в области рисования
Для задания имени области моделирования:
- дважды щелкните мышкой в области SIM Region на названии SIM2D, которое присваивается области моделирования по умолчанию. При этом открывается диалоговое окно Edit Layers;
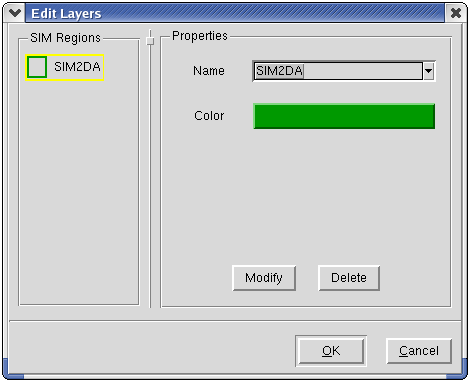
- измените имя области моделирования и цвет линии, которая эту область определяет, (по желанию);
- нажмите кнопку Modify и затем OK.
Замечание: Имя области моделирования должно обязательно содержать префикс SIM2D и состоять только из заглавных букв и цифр.
Для сохранения файла в меню File выполните команду Save.
Ligament Flow Editor
Ligament Flow Editor - программный модуль, в котором выполняется редактирование командного файла для моделирования технологического процесса. Для его запуска необходимо напечатать в командной строке окна Терминал:
> ligedit
Вид главного окна Ligament Flow Editor представлен на рис. 1.
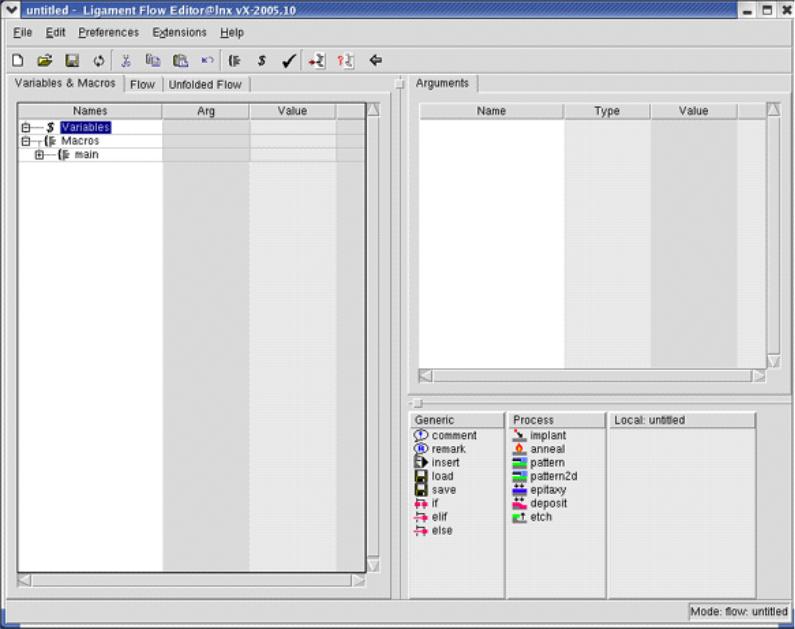
Рис.1. Графический интерфейс Ligament Flow Editor
Кроме стандартного меню и меню инструментов окно Ligament Flow Editor содержит несколько рабочих областей.
Область Flow (Процесс) расположена в левой части окна Ligament Flow Editor и отображает результат редактирования текущего процесса. В этой области имеется три закладки:
Закладка Variables & Macros (Переменные и Макросы) отображает «дерево» переменных и макросов, которое включает в себя все переменные и макросы, определенные в текущем процессе. Каждый процесс содержит, по крайней мере, один основной макрос.
Закладка Flow отображает последовательность операций процесса, представленную с помощью имен макросов.
Закладка Unfolded Flow содержит последовательность операций процесса, в которой все макросы представлены в развернутом виде, а также проверены и решены все ветвления по команде if.
Окно аргументов расположено в верхнем правом углу и отображает текущие значения аргументов выбранного макроса или переменной на вкладке аргументов.
Список макросов, имеющихся в библиотеке Ligament Flow Editor, расположен в правой нижней части панели. Все макросы для удобства сведены в таблицу, которая содержит как стандартные, описанные в приложении Ligament SPR и доступные для любых процессов в Ligament Flow Editor, так и локальные, которые определены в текущем моделируемом потоке и могут быть использованы только в нем. Библиотека включает в себя несколько подразделов:
- Панель Generic, содержит все макросы, определенные в приложении Ligament SPR, которые не являются специфическими для данного процесса, их определение не может быть изменено в Ligament Flow Editor.
- Панель Process содержит все макросы, являющиеся командами процессов и определенные в пакете Ligament SPR, определения этих макросов также не могут быть изменены.
- Панель Local содержит все определенные пользователем макросы и переменные.
Запуск нового проекта
Для запуска нового проекта в Ligament Flow Editor выберите команду New в меню File или кликните на иконку с соответствующим изображением.
Для описания среды моделирования в меню Edit выберите команду Add process header.
На вкладке Flow появятся три новых макроса: environment (среда моделирования), substrate (подложка) и comment (комментарии), как показано на рис. 2.
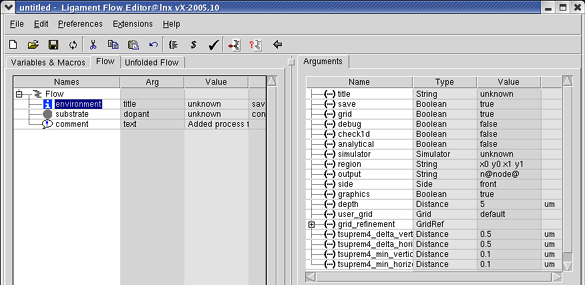
Рис. 2.
Эти макросы используются для определения начальных условий моделирования процесса, включая описание подложки, определение области моделирования и начальные условия разбиение модели на конечные элементы.
Сохранение процесса
Для того чтобы сохранить текущий процесс в меню File выберите команду Save и введите имя файла.
По умолчанию файлу присваивается расширение .cmd.
Изменение аргументов макроса.
Чтобы изменить аргументы макроса:
На вкладке Flow кликните на строчке с названием environment. Все доступные аргументы макроса отобразятся в окне аргументов в правой части экрана.
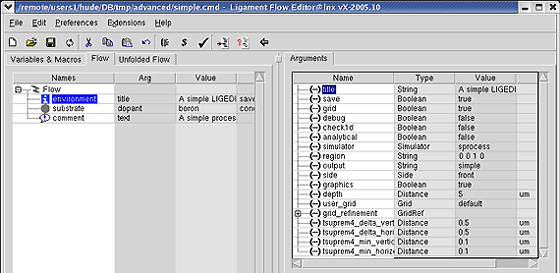
Рис. 3.
Двойной щелчок мыши на имени аргумента позволяет изменить любое значение этого аргумента. Диалоговое окно изменения значений аргумента показано на рис. 4. Для ввода большого текста используйте String Editor, кликнув на кнопке Open Text Area.
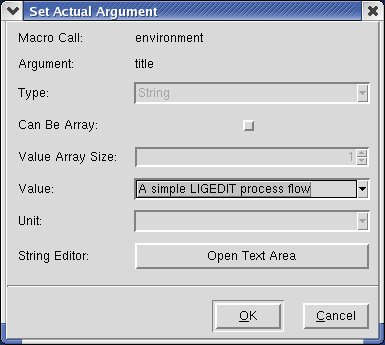
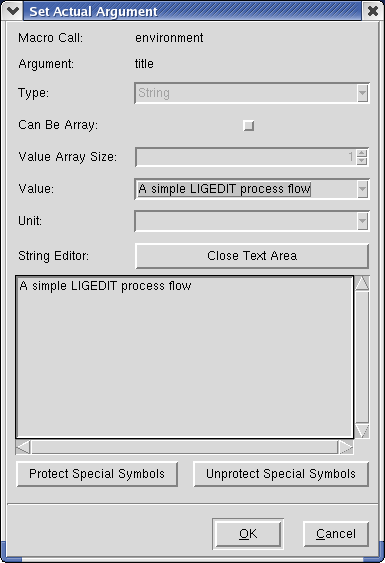
Рис. 4.
Добавление шагов процесса.
Когда описание начальных условий завершено, можно приступать к добавлению шагов процесса к общему потоку. Покажем, как это делается, на примере операции нанесения.
Для описания процесса нанесения слоев на поверхность подложки:
Добавьте к описанию процесса макрос нанесения deposit:
Перетащите макрос deposit из столбца Flow на панели Library view во вкладку Flow сразу после макроса comment, как показано на рис. 5.
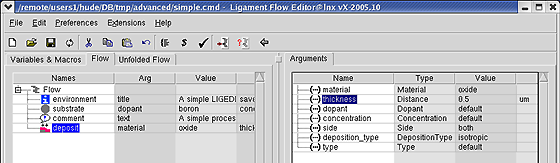
Рис. 5.
В правой части экрана откроется список текущих аргументов этого макроса. Дважды щелкнув на имени аргумента, откройте окно изменения значений аргументов макроса и измените текущие значения выбранного аргумента.
Макросы, определенные пользователем и их использование.
В Ligament Flow Editor пользователи могут создавать и определять собственные макросы. Такие макросы могут использоваться в текущем процессе наряду со стандартными макросами, которые были определены в пакете Ligament SPR.
Пользовательский макрос может содержать шаги процесса, позволяющие моделировать целый блок стандартных операций.
