Основні теоретичні відомості

Розглянемо систему двох круглих котушок, середні лінії яких лежать в паралельних площинах. Центри котушок лежать на одній лінії, перпендикулярній площинам середніх ліній. Оскільки перерізи котушок малі порівняно з радіусами котушок, ми не отримаємо при розрахунку великої похибки, якщо замінимо котушки одновитковими тонкими контурами (рис. 3.2.), які повторюють форму середніх ліній. Нехай R₁=R₂ – радіуси цих кругових контурів. Визначимо потік взаємоіндукції , який зчіплюється з другим контуром при проходженні струму по першому контуру. Вказаний потік може бути отриманий інтегруванням векторного потенціалу вздовж осі цього контуру:

.

Векторний потенціал в деякій точці на осі другого контуру визначається виразом:

,

де - вектор густини струму в центрі елементу об’єму - першого контуру; - об’єм першого контуру; - відстань від до точки, в якій визначається векторний потенціал; - магнітна проникність середовища навколо контурів (вважаємо, що в цьому середовищі відсутні феромагнетики).

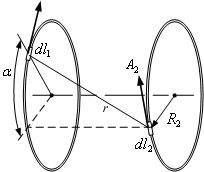
Рис. 3.2. До визначення взаємної індуктивності круглих одновиткових контурів.

Так як лінійні розміри поперечного перерізу першого контуру дуже малі порівняно з радіусом самого контуру, можна обмежитись поділом об’єму цього контуру тільки по довжині на нескінченно малі відрізки і представити у вигляді:

.

В такому випадку маємо:

і

,

де інтегрування проводиться вздовж всього першого контуру.

Внаслідок симетрії відносно осі ОХ лінії векторного потенціалу повинні бути колами, що лежать в площинах, паралельних площині контуру, і мати центри на осі ОХ. Векторний потенціал має напрям по дотичній до цих кіл, тобто має тільки одну складову:

.

Оскільки і , то

Даний інтеграл зводиться до табличних еліптичних інтегралів:

,

де ; - повні еліптичні інтеграли першого і другого роду. В цих інтегралах:

і .

Отже, рівняння векторного потенціалу можна записати у вигляді:

.

В додатках наведені графіки залежності від .

Оскільки вектор потенціалу дотичний до контуру по всій його довжині і має сталу величину, то:

,

або

.

Повне потокозчеплення двох котушок з витками , та струмом першої дорівнює:

.

Отже, взаємну індуктивність круглих плоских котушок можна визначити з виразу:

.

Для визначення взаємної індуктивності квадратних плоских котушок також замінимо їх тонкими одновитковими контурами (рис. 3.3.) та скористаємось методом ділянок. Розкладемо кожний контур на чотири прямолінійні ділянки і позначимо довжину кожної . Нехай - порядковий номер ділянки першого контуру, а - порядковий номер ділянок другого контуру. Взаємна індуктивність контурів:

,

де

.

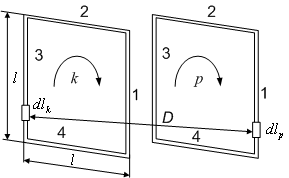
Рис. 3.3. До визначення взаємної індуктивності квадратних одновиткових контурів.

Величина являє собою взаємну індуктивність між -им відрізком першого контуру та -им відрізком другого контуру, - довжина сторони контуру, - відстань між відрізками. Знак взаємної індуктивності визначається напрямами обходу контурів: якщо напрями співпадають, значення додатне, в іншому випадку – від’ємне. Оскільки для взаємно перпендикулярних відрізків , фактична взаємна індуктивність двох квадратних плоских контурів визначається з виразу:

.

Повертаючись від одновиткових контурів до котушок:

.