Программа (схема) работы машины Тьюринга,

реализующей алгоритм примера 10.7

Состояние машины Тьюринга	Последовательность букв внешнего алфавита (слова)
	0	1

В заключение необходимо отметить, что созданная нами машина Тьюринга может применяться не только к словам в алфавите , представляющим собой записанные подряд единиц при . Она применима и ко многим другим словам в этом алфавите, например,: 1011, 10011, 111011, 11011, 1100111, 1001111, 10111, 10110111 и т.д. (исходя из стандартного начального положения у первой единицы справа).

Однако оказывается, что она неприменима к ряду слов, отвечающих условию , то есть при подаче этих слов она будет работать вечно, вместо того, чтобы остановиться. Например, она неприменима к следующим словам: 101, 1001, 11101, 101101, 1100101101 и т.д.

Рассмотрим работу машины применительно к слову 1001. Конфигурации работы приведены ниже.

; ; ;

; ; и т.д.

10.2. Задания к выполнению работы

Применение машин Тьюринга к словам

1. Определить, какую функцию вычисляет машина Тьюринга с программой команд, представленных в таблице:

Состояние машины

2. Убедиться, что машина с алфавитом и программой

Состояние машины

каждое слово длины алфавита перерабатывает в слово длины r ( r – остаток от деления числа на 3).

3.Рассмотреть, как работает машина Тьюринга, заданная функциональной схемой (табл.10.5),

Таблица 10.5

Состояние машины Тьюринга	Последовательность букв внешнего алфавита (слова)

и показать в соответствии с вариантом задания все конфигурации тактов работы машины до их повторения или останова, если начальная конфигурация имеет вид, определенный табл. 10.6.

Таблица 10.6

Начальные конфигурации машины Тьюринга

№ варианта	Начальная конфигурация	№ варианта	Начальная конфигурация
1		16
2		17
3		18
4		19
5		20
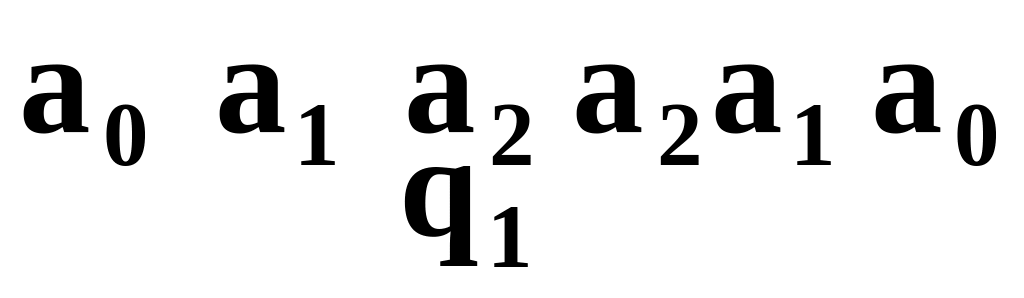
6		21
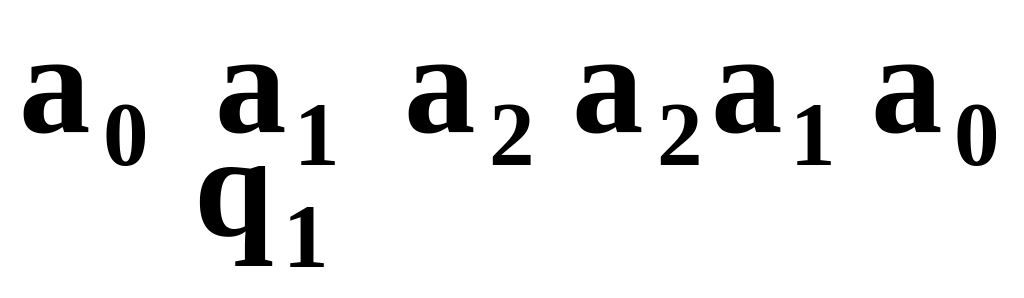
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Конструирование машин Тьюринга

1. Построить в соответствии с заданным вариантом машину Тьюринга, реализующую алгоритм вычисления функций, представленных в табл. 10.7. Записать все конфигурации тактов работы машины при равном номеру варианта задания.

Таблица 10.7

Функции для построения схем(программ) машин Тьюринга

№ варианта		№ варианта		№ варианта
1		11	0	21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

2. Построить машину Тьюринга, которая из подряд записанных единиц оставляла бы на ленте единицы, также записанных подряд, если , и работала бы вечно, если или .

3. Построить машину Тьюринга, которая применима ко всем словам в алфавите и делает следующее: любое слово , где или ( ), преобразует в слово .

4. Построить машину Тьюринга для вычисления функции

5. Построить машину Тьюринга для вычисления функции

6. Записать в алфавите программу работы машины Тьюринга для вычисления функции