8.2. Задания к выполнению работы

1. Какие из следующих выражений являются формулами исчисления высказываний:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) .

2.2. Выписать все подформулы формул:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) .

2.3. Для формул , , , записать результаты каждой из следующих подстановок:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) .

Решение примера 1.

.

2.4. Показать, доказуемость нижеследующих формул, применяя правило подстановки:

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. .

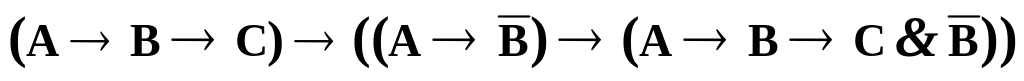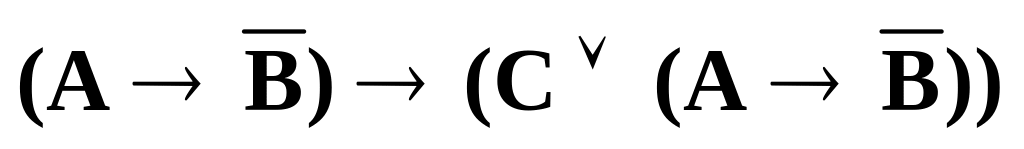Решение примера 1.

Для решения подобных примеров необходимо подобрать соответствующую аксиому из четырех групп аксиом, которые все являются доказуемыми формулами, и найти такие подстановки переменных, которые приведут к необходимой формуле. В частности для данного примера необходимо взять аксиому I₁ и вместо надо подставить выражение , а вместо –

.

2.5. Показать, доказуемость нижеследующих формул, применяя правило подстановки и правило заключения:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) .

Решение примера 1.

Для решения подобных примеров необходимо подобрать соответствующую аксиому из четырех групп аксиом, таким образом, чтобы после проведения подстановки можно было применить либо правило заключения

├

.

А; ├ А→В

├В

либо правило сложного заключения

├

.

├ ,…,├ ;├

├

1) Возьмем аксиому I₁

и сделаем в ней подстановку . Получим доказуемую формулу

├ ,

в которой можно выделить две части: доказуемую формулу =├ (аксиома II₁ ) и еще недоказанную формулу .

2) Применяя правило заключения,

├

.

;├

├

получим доказуемую формулу ├ .

2.6. Показать, доказуемость нижеследующих формул, применяя производные правила вывода.

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) .

Решение примера 1.

Для решения подобных примеров необходимо так же, как и в предыдущих заданиях, подобрать соответствующую аксиому из четырех групп аксиом, произвести подстановку таким образом, чтобы можно было применить производные правила вывода, после осуществления которых применяют либо правило заключения, либо правило сложного заключения.

1) Возьмем аксиому III₃

и сделаем подстановку , получим доказуемую формулу ├ .

2) Покажем доказуемость формул и . Для этого берем аксиомы II₁ и II₂ и применяем к ним подстановку и , получим ├ и ├ . Далее применяем к ним правило контрпозиции

├

,

, ├

├ ├

получим доказуемые формулы ├ и ├ .

3) Теперь можно применить правило сложного заключения

├ ,├ ;├ .

├

Получим доказуемую формулу .

2.7. Доказать, что

1) ├ ;

2) ├ ;

3) ├ ;

4) ├ ;

5) ├ ;

6) ├ ;

7) ├ ;

8) ├ ;

9) ├ ;

10) ├ .

Решение примера 1.

1) Так как по условию задачи формула принадлежит ( ), то по определению выводимой формулы она доказуема

├ .

2) На основании аксиомы I₁ и подстановки получим доказуемую формулу, которая выводима из по определению выводимой формулы

├ .

3) Применяя правило заключения

,

├ ;├

├

получим доказуемую формулу

├ .

В итоге запишем вывод из : , , .

Решение примера 2.

1) Так как по условию задачи совокупности принадлежат доказуемые формулы и , то, применяя правило силлогизма

├

,

А → В; ├ В → С

├ А → С

получим доказуемую формулу . Вывод из запишется так: : , , .

2.8. Показать доказуемость нижеследующих формул, применяя обобщенную теорему дедукции:

1) ;

2) ;

3)

Решение примера 1.

Возьмем совокупность формул

и докажем, что ├ . Запишем для этого вывод из : . Тогда по обобщенной теореме дедукции, заключающейся в том, что если существует доказуемая формула , выводимая из объединения совокупностей , то существует и доказуемая формула , выводимая из совокупности

,О

├

├

получим ├ .

2.9. Показать, что справедливы законы логики (доказуемы формулы):

1) ; 2) ; 3) .

Решение примера 1.

1) Сделаем подстановки в аксиомы I₁ и IV₁

и .

В результате получим доказуемые формулы

├ ,

├ .

2) Из этих формул по правилу силлогизма (если доказуемы формулы А → В и В → С, то доказуема и формула А → С) следует:

├ .

3) Используя закон соединения посылок (если формула доказуема, то доказуема и формула , полученная из исходной путем объединения посылок и ), получим

├ .

4) Используем правило снятия двойного отрицания (если доказуема формула , то доказуема формула , и если доказуема формула , то доказуема формула ), получим

├ .

5) И в итоге применим правило разъединения посылок (если формула доказуема, то доказуема и формула , полученная из исходной путем разъединения посылок и ), получим доказуемую формулу

├ .

2.10. Используя правила перестановки посылок, соединения посылок и разъединения посылок, доказать, что

1) ├ ;

2) ├ ;

3) ├ .

2.11. Доказать производные правила вывода:

;

1)

2)

3)

;

;

├ ├ ├

├ ├ ├

;

4)

5)

6)

;

;

├ ├ ├

├ ├ ├

;

7)

8)

9)

;

;

├ ,├ ├ ,├ ├ ,├

├ ├ ├

;

10)

11)

12)

;

;

├ ,├ ├ ├

├ ├ ├

;

13)

14)

.

├ ,├ ├ ,├

├ ├

Решение примера 1.

1) По условию формула доказуема, то есть ├ .2) Используем аксиому II₁ и подстановку ,получим ├ .

3) Применим к данной формуле правило контрпозиции (если доказуема формула , то доказуема формула ). Получим

├ .

4) Из формул п. 1 и п. 3 по правилу заключения (если формулы и доказуемы, то формула также доказуема) получим ├ . Таким образом, пример 1 доказан.

2.12. Дана формула и наборы значений переменных. Записать вывод формулы или ее отрицания из соответствующей совокупности формул

1) . Наборы переменных: 1) (0, 0, 1); 2) (1, 0, 0).

2) . 1) (1, 1, 1); 2) (1, 0, 1); 3) (0, 1, 0).

3) . 1) (1, 0, 0); 2) (0, 1, 1).

Решение примера 1.

1) ├ . Вывод:

.

2) ├ . Вывод:

.
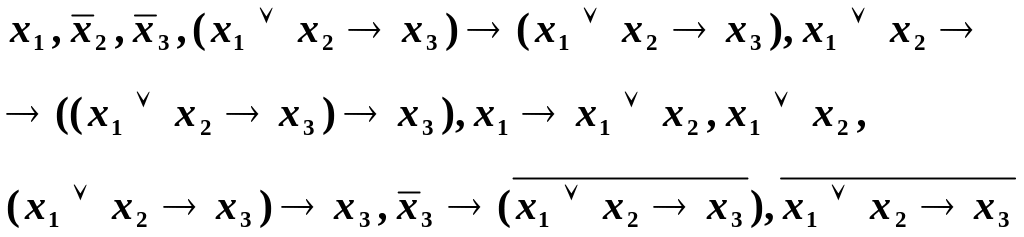