4.1.2. Реализация с помощью релейно-контакных схем основных логических операций

Рассмотрим переключательные схемы РКС, реализующие основные логические операции, и схемы, реализующие различные булевы формулы, и найдем их функции проводимости.

РКС, реализующая логическую операцию конъюнкции.

На рис. 4.2 представлена переключательная схем, реализующая операцию конъюнкции.

Первая схема (рис. 4.2 а) состоит из двух последовательно соединенных контактов и , связанных с двумя переключателями, каждый из которых срабатывает независимо от другого. На рис. 4.2 б) показано условное графическое обозначение переключательной схемы, реализующей операцию конъюнкции.

Очевидно, что данная схема проводит электрический ток тогда и только тогда, когда оба контакта и замкнуты, то есть только тогда, когда обе переменные и принимают значение 1.

Таким образом, функция проводимости РКС, состоящей из двух последовательно соединенных контактов (переключателей) и , является конъюнкция .

Можно сказать, что последовательное соединение двух контактов (переключателей) реализует конъюнкцию соответствующих этим контактам булевых переменных.

РКС, реализующая логическую операцию дизъюнкции

На рис. 4.3 представлена переключательная схема, реализующая операцию дизъюнкции.

Эта схема состоит из двух параллельно соединенных переключателей и .

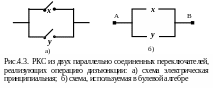
Показанная на рис.4.3 схема проводит электрический ток в том и только в том случае, когда, по меньшей мере, один из контактов и замкнут, то есть лишь в случае, когда хотя бы одна из булевых переменных принимает значение 1.

Булева функция от двух аргументов и , удовлетворяющая этому условию, является дизъюнкция . Таким образом, функцией проводимости РКС, состоящей из двух параллельно соединенных контактов и , является дизъюнкция .

Говорят, что параллельное соединение двух контактов (переключателей) реализует дизъюнкцию соответствующих этим контактам булевых переменных.

Таким образом, с помощью РКС можно реализовать конъюнкцию, дизъюнкцию, отрицание.

Учитывая, что всякая булева функция с помощью равносильных преобразований может быть представлена как суперпозиция конъюнкции, дизъюнкции и отрицания переменной, то она может быть реализована с помощью РКС. Реализуем таким образом импликацию и эквивалентность.

Для этого выразим их с помощью равносильностей из второй группы через конъюнкцию, дизъюнкцию и отрицание и уже далее составим схему следуя изученному способу.

Импликация

Для импликации равносильность дает следующее преобразование

,

которое может быть реализовано в виде схемы на рис. 4.4.

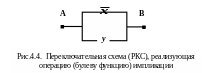
Эквивалентность

Для эквивалентности равносильность дает следующее преобразование

.

Получены две импликации, для каждой из которых можно использовать составленную выше схему на рис.4.4, получим схему операции эквивалентности (рис.4.5).

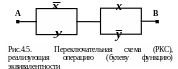
Из схем, представленных на рис. 4.1 – 4.5, путем их последовательного и параллельного соединения могу быть построены новые двухполюсные переключательные схемы, которые называют П–схемами. Таки образом, всякая формула алгебры логики (булева функция) может быть изображена П–схемой и, обратно, для любой П–схемы может быть записана формула (булева функция), которая реализуется данной схемой.

Две основные задачи теории релейно-контактных схем

Составление РКС с заданными условиями работы называется задачей синтеза РКС и является первой важной задачей, состоящей в том, что требуется построить схему, которая проводила бы электрический ток лишь при вполне определенных задаваемых условиях.

Очевидно, что всегда для каждой булевой функции необходимо выбирать самую простую РКС, для того чтобы минимизировать затраты на ее изготовление. Поэтому упрощение РКС называется задачей минимизации или задачей анализа таких схем и является второй важной задачей теории релейно-контактных схем.

Две РКС, составленные из одних и тех же переключателей, называются равносильными, если одна из них проводит ток тогда и только тогда, когда другая схема проводит ток.

Иначе говоря, две схемы, составленные из одних и тех же реле, равносильны, если они обладают одинаковыми функциями проводимости, зависящими от одних и тех же переменных. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов.

Обычно она решается следующим образом. Для данной РКС записывается ее функция проводимости. Затем она упрощается с помощью тождественных преобразований и сводится к функции, имеющей меньшее число вхождений (повторений) переменных, чем исходная функция. И после этого строится РКС, реализующая полученную упрощенную булеву функцию.

Приведем примеры построения РКС по исходной булевой функции, нахождения булевой функции по имеющейся РКС, а также примеры минимизации и проверки равносильности РКС.

Пример 4.1

Построить РКС по формуле .

Видно, что две конъюнкции связаны дизъюнкцией, отсюда схема будет иметь следующий вид (рис.4.6):

Пример 4.2

Построить РКС по формуле .

Здесь уже четыре конъюнкции трех переменных связаны дизъюнкцией, отсюда схема будет иметь следующий вид (рис.4.7):

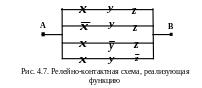
Но исходную формулу можно вначале упростить (минимизировать) и уже потом по новой упрощенной формуле построить более простую РКС. Выполним это.

На основании минимизированной формулы построим новую упрощенную схему (рис. 4.8).