Численные методы решения прямых и обратных задач гравиразведки

Для объектов сложной формы, создающих аномалии, прямые задачи гравиразведки решаются численными методами. Численные методы сводятся к разбиению объекта на элементарные массы – ячейки, например, шаровой или кубической формы. Гравитационный эффект таких масс рассчитывается по формуле (1.4), а затем ведется их суммирование по всему объему объекта.

Обратные задачи решаются методом сравнения наблюдаемой аномалии с аномалиями, рассчитанными теоретически. При расчете выполняется перебор вероятных значений геометрических параметров и избыточной плотности до получения наименьших расхождений между наблюденной и теоретической кривой.

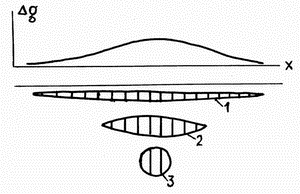
Решения обратных задач гравиразведки, как и всех обратных задач математической физики, неоднозначны. На рис. 1.3 приведен схематический пример того, как объекты разного сечения и глубины залегания, даже при одинаковой избыточной плотности, могут создать одинаковую аномалию силы тяжести.

Рис.1.3 Пример неоднозначности решения обратной задачи гравиразведки: 1-3 – объекты, создающие аномалию

Для практических занятий. Прямая и обратная задачи над шаром

1. Прямая задача. Пусть однородный шар радиуса и плотности 𝜎 расположен на глубине h в среде с плотностью 𝜎₀. Для простоты расчетов центр шара находится на оси z, а наблюдения проводятся по оси x) (рис. 1.3).

Рис.1.3 Гравитационное поле шара

Формула для вычисления g может быть получена из (1.3) путем замены элементарной массы dm массой шара в силу того, что притяжение однородным шаром происходит так, как если бы вся масса была сосредоточена в центре шара. Учтя, что x'=y'=0,z'=h, x=y=z=0, r=(x²+h²)^1/2 , получим для шара

(1.5) График g будет иметь максимум над шаром (x=0) и асимптотически стремиться к нулю при удалении от шара. В плане изолинии g будут иметь вид концентрических окружностей.