Пример решения транспортной задачи

Дано: Пусть три поставщика обеспечивают сырьем четыре предприятия. Предложения поставщиков равны 160, 140 и 170 т. спрос на сырье каждого предприятия составляет 120, 50, 190 и 110 т. На каждое предприятие сырье может завозиться от любого поставщика. Тарифы перевозок известны и задаются в таблице (в у.е./т):

	Предприятие 1	Предприятие 2	Предприятие 3	Предприятие 4
Поставщик 1	7	8	1	2
Поставщик 2	4	5	9	8
Поставщик 3	9	2	3	6

Требуется составить план перевозок, при котором общая стоимость перевозок минимальна.

Построение математической модели

Критерий оптимизации (минимум транспортных расходов) задается функцией:

F=7x₁₁+8x₁₂+x₁₃+2x₁₄+4x₂₁+5x₂₂+9x₂₃+8x₂₄+9x₃₁+2x₃₂+3x₃₃+6x₃₄  min

Система ограничений записывается как:

x₁₁+x₁₂+x₁₃+x₁₄=160

x₂₁+x₂₂+x₂₃+x₂₄=140

x₃₁+x₃₂+x₃₃+x₃₄=170

x₁₁+x₂₁+x₃₁=120

x₁₂+x₂₂+x₃₂=50

x₁₃+x₂₃+x₃₃=190

x₁₄+x₂₄+x₃₄=110

x_ij  0, i=1, 2, …m, j=1, 2, …n.

Ограничения имеют вид равенств, поскольку имеет место равенство между суммарным предложением и суммарным спросом 120+50+190+110=160+140+170.

Решение с использованием ms excel

1. Откройте новый рабочий лист и внесите на него исходные данные так, как это показано на рис. 2.1.

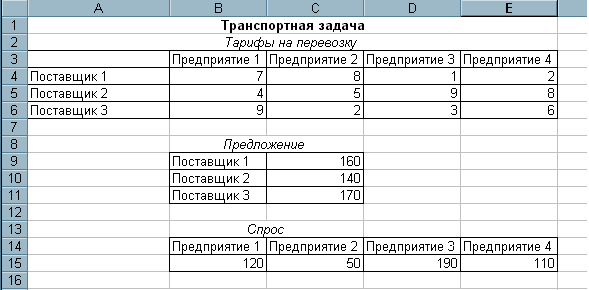
Рис.2.1

2. Подготовьте таблицу для решения задачи, задайте целевую функцию и ограничения (см. рис.2.2).

• В диапазоне (В19:E21) будет получено решение (оптимальный план перевозок).

• В ячейку B23 записывается формула для вычисления значений целевой функции - =СУММПРОИЗВ(B4:E6;B19:E21).

• В ячейки В25-В31 записываются левые части ограничений (2.2) и (2.3).

• В ячейки D25-D31 записываются правые части ограничений (2.2) и (2.3).

Рис.2.2

3. Вызовите подпрограмму Сервис-Поиск решения. В открывшемся окне «Поиск решения» (см. рис.2.3) задайте:

• В поле Установить целевую ячейку задайте адрес B23.

• Установите переключатель в положение Минимальному значению.

• В поле Изменяя ячейки задайте адрес диапазона плана перевозок В19:E21.

• В окне Ограничения удалите все ограничения, оставшиеся от решения предыдущей задачи (выделите и удалите по одному с помощью кнопки Удалить). После этого добавляйте ограничения по одному с помощью кнопки Добавить.

  • Нажмите кнопку Добавить.

  • В открывшемся окне «Добавление ограничения» (рис.2.3) в поле Ссылка на ячейку задайте ячейку, содержащую формулу левой части ограничения (например В25). В списке выберите знак «=». В поле Ограничение задайте ячейку, содержащую правую часть ограничения (например D25).

  • Нажмите кнопку ОК.

• После добавления всех ограничений нажмите кнопку Параметры и перейдите к окну «Параметры поиска решения». Установите флажок в поле Неотрицательные значения (для выполнения ограничения (2.4)). Установите флажок в поле Линейная модель.

• Нажмите кнопку ОК в окне «Параметры поиска решения».

• Нажмите кнопку Выполнить в окне«Поиск решения».

• Результаты работы подпрограммы Поиск решения отображаются в окне «Результаты поиска решения». Сообщение «Решение найдено. Все ограничения и условия оптимальности выполнены.» свидетельствует о корректном завершении задачи. В этом случае нажмите кнопку ОК и проанализируйте полученный в диапазоне (В19:E21) оптимальный план перевозок. Если появляется сообщение «Поиск не может найти подходящего значения», нажмите кнопку Отмена и проверьте правильность исходных данных и ограничений.

Рис.2.3. Описание математической модели в окне «Поиск решения»

4. Проанализируйте полученное решение (см. рис.2.4).

• Оптимальный план перевозок содержится в диапазоне В19:E21.

• Все ограничения, имеющие в случае сбалансированной транспортной задачи вид строгих равенств, выполнены.

• Минимальная стоимость перевозок составляет 1330 у.е.

5. Постройте и отформатируйте диаграмму, показывающую долю поставщиков продукции в удовлетворении спроса предприятий (см. рис. 2.5).

Рис. 2.4. Решение транспортной задачи

Рис.2.5. Оптимальная структура производства