Один за другим послано 3 радиосигнала. Вероятности приёма каждого из них не зависят от того, приняты ли остальные сигналы, и равны 0,6. Случайная величина X – число принятых сигналов. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).
В семье трое детей: 2 мальчика и 1 девочка. Наугад выбраны двое детей. Случайная величина X – число мальчиков среди выбранных детей. Найти: а) ряд распределения; б) M(X), D(X).
Случайная величина X имеет плотность распределения
.
Найти: 1) параметр с; 2) функцию распределения F(x); 3) P(X > 0); 4) математическое ожидание M(X) и дисперсию D(X). Построить графики функций F(x) и f(x).
Случайная величина X распределена по нормальному закону с параметрами a и . Даны математическое ожидание M(X) = – 2 и дисперсия D(X) = 4. Найти: а) параметры a и ; б) вероятности P( – 5 X – 2 ) и P ( | X – a | < 6 ); в) значение x из условия P(X x) = 0,05. Построить графики функций f(x), F(x) и показать на них геометрический смысл P( – 5 X – 2 ).
В ящике 2 белых и 2 чёрных шара. Наугад выбирают 2 шара. Случайные величины: X – число чёрных шаров;
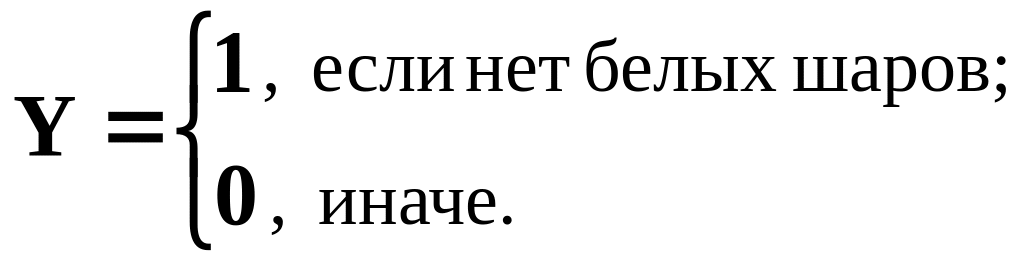
Найти: а) законы распределения для X и Y; б) закон распределения для двумерной величины (X, Y) ;
в) основные характеристики: M(X), M(Y), D(X), D(Y), r(X, Y).
Составил Зайцев В. П.
АлтГТУ им. И.И. Ползунова
Кафедра высшей математики
Индивидуальное задание для студентов 2 курса (4-й семестр)
Вариант № 16
Случайные события
За круглый стол произвольно сели двое мужчин и две женщины. Найти вероятность того, что при этом мужчины будут чередоваться с женщинами.
На отрезок [ 0, 5 ] случайно бросаются две точки. Найти вероятность того, что сумма квадратов их расстояний от левого конца отрезка превысит 4.
В урне 14 шаров, среди которых 9 белых и 5 чёрных. Наудачу извлекают 4 шара. Определить вероятность того, что: а) все шары белого цвета; б) 2 шара белых, а остальные чёрные; в) все шары одного цвета.
В студенческой группе 15 юношей и 10 девушек. На концерт группе дали 5 билетов, которые разыгрываются по жребию. Какова вероятность, что на концерт попадут 2 девушки и 3 юноши?
Два человека А и В играют в следующую игру: на шахматную доску с размерами квадратов 5 х 5 см. бросается копеечная монета диаметром в 1,5 см. Если монета упадёт целиком внутри какой-нибудь клетки, то выигрывает А, если же она пересечёт хотя бы одну из сторон какого-нибудь квадрата, то выигрывает В. Кто имеет больше шансов на выигрыш?
Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производятся до первого наступления события. Определить вероятность того, что придется проводить 3 опыта.
В цехе работают два станка. Производительность 1-го станка в 3 раза больше производительности 2-го. Вероятность брака для 1-го станка равна 2%, для 2-го – 3%. Наугад взятая деталь оказалась бракованной. Какова вероятность, что эта деталь сделана на 2-м станке?
Событие B наступает в том случае, если событие А появится не менее 2-х раз. Определить вероятность появления события В, если вероятность появления события А в каждом опыте равна 0,3 и произведено 3 независимых опыта
Вероятность пробоя конденсатора во время испытаний равна 0,01. Какова вероятность того, что из 100 конденсаторов не выдержат испытания более двух?
Случайные величины
Два раза бросают одновременно 2 игральные кости. Случайная величина X – число выпадений чётного числа очков на 2-х игральных костях. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).
У охотника 3 патрона. Вероятность попасть в цель при 1-м выстреле равна 0,4, при 2-м равна 0,8, при 3-м равна 0,6. Увидев цель, охотник стреляет по ней, пока не попадёт или пока не кончатся патроны. Случайная величина X – число произведённых выстрелов (считать, что охота состоялась). Найти: а) ряд распределения; б) M(X), D(X).
Случайная величина X имеет функцию распределения
.
Найти: 1) параметр с; 2) функцию плотности f(x); 3) P(0 < X < 1,5); 4) математическое ожидание M(X) и дисперсию D(X). Построить графики функций F(x) и f(x).
Случайная величина X равномерно распределена на [a, b]. Дано математическое ожидание M(X) = 3 и дисперсия D(X) =
.
Найти: а) значения параметров a,
b;
б) функцию плотности f(x)
и функцию распределения F(x);
в) вероятность
попадания случайной величины X
на отрезок
[2, 5].
Построить графики функций f(x)
и F(x)
и показать на них геометрический смысл
P
(2
X
5).Дважды бросается монета. Случайные величины: X – число появлений «герба»;
Найти: а) законы распределения для X и Y; б) закон распределения для двумерной величины (X, Y);
в) основные характеристики: M(X), M(Y), D(X), D(Y), r(X, Y).
Составил Зайцев В. П.
АлтГТУ им. И.И. Ползунова
Кафедра высшей математики
Индивидуальное задание для студентов 2 курса (4-й семестр)
Вариант № 17
Случайные события
Найти вероятность того, что дни рождения двух человек приходятся на разные месяцы года.
На отрезок [ 0, 4 ] случайно бросаются две точки. Найти вероятность того, что сумма квадратов их расстояний от левого конца отрезка превысит 16.
В урне 9 шаров, среди которых 6 белых и 3 чёрных. Наудачу извлекают 3 шара. Определить вероятность того, что: а) все шары белого цвета; б) 2 шара белые; в) все шары одного цвета.
Десять человек, в том числе А и В, располагаются за круглым столом в случайном порядке. Какова вероятность, что между А и В будет сидеть один человек?
В круг радиуса R вписан правильный треугольник. Какова вероятность того, что наугад взятая точка из круга не окажется внутри треугольника?
Из 10 стрелков 5 попадают в мишень с вероятностью 0,8, 3 – с вероятностью 0,6, 2 – с вероятностью 0,7. Наудачу выбранный стрелок в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок?
Вероятность улучшения спортсменом личного достижения по прыжку в высоту равна p при каждой попытке. Чему равна вероятность того, что он улучшит свой результат, если ему будет предоставлена возможность прыгать 2 раза?
Каждый из пяти станков цеха может быть выключен с вероятностью 0,8. Определить вероятность того, что в цехе работают не менее четырёх станков.
В партии 1% изделий дефектных. Найти вероятность того, что среди 100 изделий, взятых наугад из этой партии, ровно 2 окажутся дефектными.
Случайные величины