На пути движения автомобиля 3 светофора. Каждый из них с вероятностью 0,8 разрешает дальнейшее движение. Случайная величина X – число светофоров, перед которыми автомобиль останавливался. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).
Имеется 10 лампочек, среди которых 4 дефектные. Случайным образом без возвращения выбрали 3 лампочки для проверки. Случайная величина X – число дефектных лампочек в выборке. Найти: а) ряд распределения; б) M(X), D(X).
Случайная величина X имеет плотность распределения
.
Найти: 1) параметр с; 2) функцию распределения F(x); 3) P(– 2 < X < 0,5); 4) математическое ожидание M(X) и дисперсию D(X). Построить графики функций F(x) и f(x).
Случайная величина X распределена по показательному закону с параметром . Дано математическое ожидание M(X) =
.
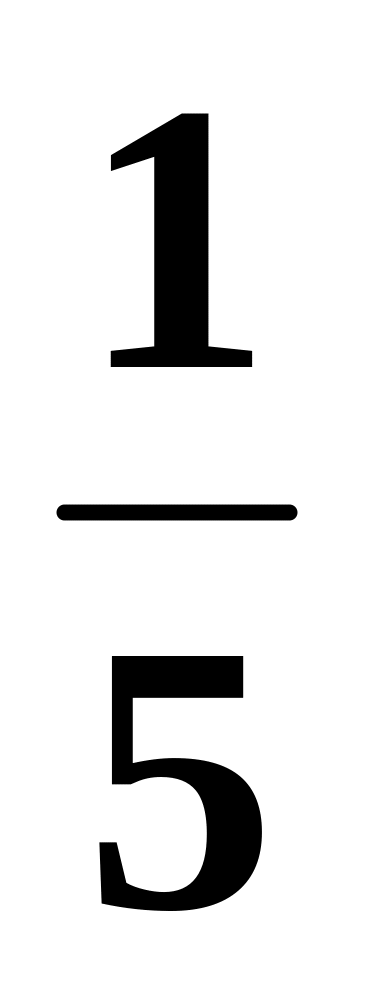Найти: а) параметр ;
б) дисперсию D(X);
в) функцию плотности f(x)
и функцию распределения F(x);
г) вероятность
попадания случайной величины X
на отрезок
[0; 1,5].
Построить графики функций f(x),
F(x)
и показать
на них геометрический смысл
P
(0
X
1,5).Из полного набора костей домино (28 штук) наугад взяли 2 кости. Случайные величины:
Y
– число «шестёрок» на выбранных костях
домино.
Найти: а) законы распределения для X и Y; б) закон распределения для двумерной величины (X, Y);
в) основные характеристики: M(X), M(Y), D(X), D(Y), r(X, Y).
Составил Зайцев В. П.
АлтГТУ им. И.И. Ползунова
Кафедра высшей математики
Индивидуальное задание для студентов 2 курса (4-й семестр)
Вариант № 30
Случайные события
У игральных костей противоположные грани закрашены в одинаковые цвета: зелёный, красный, жёлтый. Подбрасываются три кости. Какова вероятность, что хотя бы две верхние грани окажутся одного цвета?
В промежутке времени [ 0, T ] случайно приходят два сигнала длительностью T1 и T2. Найти вероятность того, что они не перекрываются, если T = 1 мин.; T1 = 10 сек., T2 = 8 сек. Сделать чертёж.
В урне 15 шаров, среди которых 9 белых и 6 чёрных. Наудачу извлекают 5 шаров. Определить вероятность того, что: а) все шары белого цвета; б) 3 шара белые, а остальные чёрные; в) все шары одного цвета.
На стоянке для автомобилей можно поместить 6 машин в один ряд. В какой-то момент времени оказались заняты 3 места. Какова вероятность, что все свободные места следуют одно за другим?
Поступило сообщение о том, что при перевозке 8-ми изделий типа A и 10-ти изделий типа В были повреждены 2 изделия. Найти вероятность того, что были повреждены изделия одного типа.
Вероятность попадания в самолёт равна 0,4, а вероятность сбить самолёт равна 0,1. Найти вероятность того, что при попадании в самолёт он будет сбит.
Имеется два ящика: в первом 4 белых шара и 2 чёрных, а во втором 3 белых и 3 чёрных. Из первого ящика во второй перекладывают, не глядя, 2 шара. После этого из второго ящика берут наугад один шар. Найти вероятность того, что этот шар будет белым.
Рабочий обслуживает 5 станков, каждый из которых за смену может потребовать внимание рабочего с вероятностью 0,25. Найти вероятность того, что за смену потребуют внимание рабочего не менее трёх станков.
Пять работниц окрашивают одинаковые игрушки: две в красный цвет, а три - в зелёный. Производительность труда одинаковая. Окрашенные игрушки складываются в один ящик. Определить вероятность того, что среди 600 игрушек красных окажется от 230 до 260.
Случайные величины
Вероятность выигрыша по одному лотерейному билету равна 0,1. Случайная величина X – число выигрышных билетов среди 4–х купленных билетов. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).
В пакете 5 плодов: 2 яблока и 3 груши. Наугад берутся 3 плода. Случайная величина X – число взятых груш. Найти: а) ряд распределения; б) M(X), D(X).
Случайная величина X имеет функцию распределения
Найти: 1) параметр с; 2) функцию плотности f(x); 3) P(4 < X < 5); 4) математическое ожидание M(X) и дисперсию D(X). Построить графики функций F(x) и f(x).
Случайная величина X распределена по нормальному закону с параметрами a и . Даны математическое ожидание M(X) = 1 и дисперсия D(X) = 1. Найти: а) параметры a и ; б) вероятности P( – 3 X 0,5 ) и
P ( | X – a | < 1,5 ); в) значение x из условия P(X x) = 0,1. Построить графики функций f(x), F(x) и показать на них геометрический смысл P( – 3 X 0,5 ).
В кошельке 7 денежных купюр: пять по 10 рублей, одна – 50 рублей и одна – 100 рублей. Наугад взяли две купюры. Случайные величины: X – сумма (в рублях); Y – число десяти рублёвых купюр среди выбранных.
Найти: а) законы распределения для X и Y; б) закон распределения для двумерной величины (X, Y) ;
в) основные характеристики: M(X), M(Y), D(X), D(Y), r(X, Y).
Составил Зайцев В. П.